- •1.Снарядтың ұшу траекториясын бірінші ретті дифференциалдық теңдеулер жүйесімен берілген Коши есебімен модельдеу.
- •2.Гармониялық тербелістің фазалық жазықтағы сипаттамасын математикалық модельдеу.
- •3.Математикалық маятниктің тербелісін модельдеу.
- •4.Ферхюльстің математикалық моделі.
- •5.“Жыртқыш-Жемтік” математикалық моделі.
- •6.Вольтерр-Лотка теңдеуінің фазалық жазықтықтағы сипаттамасы.
- •7.“Жыртқыш-Жемтік” математикалық моделінің кинематикалық сипаттамасы.
- •8.Көптүйіліскен аймақ үшін сығылмайтын сұйықтың фильтірлену есебінің математикалық моделі.
- •9.Мятиев -Гиринский математикалық моделін қорыту және механикалық мағанасы.
- •10.Хантуш математикалық моделін қорыту және механикалық мағанасы.
- •9) Ракетаның ұшу траекториясын бірінші ретті дифференциалдық теңдеулер жүйесімен берілген Коши есебімен модельдеу.
- •11.Толық электрлік тізбектің математикалық моделі
- •13)Тұтқырлық үйкеліс күштің әсеріне байланысты тербелісті модельдеу.
- •§2. Қозғалыс теңдеуін Ньютонның тұтқырлық заңын ескеріп жазу.
- •14)Тербелісті сипаттайтын модельдің Эйлер сандық шешімі.
- •20)Келтірілген пластық қысымға түсінік.
- •24. Сығылмайтын сұйықтың фильтірлену математикалық моделінің Пуассон теңдеуі және дельта функцияның сипаттамасы.
- •26. Мятиев-Гиринский математикалық модельнің сандық шешімінің интегралдық баланыс теңдеуін қорыту және механикалық мағанасы.
- •Дарси заңы:
- •Флюид күйін сипаттайтын теңдеу:
- •Кеуек орта:
- •27.Тұтқырлы пластикалық сұйықтың фильтірлену жылдамдығының математикалық моделі.
- •28.Тұтқырлы пластикалық сұйықтың фильтірлену пьезоөткізгіштік математикалық моделі.
- •31.Ньютондық емес сұйықтың фильтірлену жылдамдығының математикалық моделін қорыту.
- •31.Ньютондық емес сұйықтың фильтірлену жылдамдығының математикалық моделін қорыту.
- •32. Ньютондық емес сұйықтың фильтірлену пьезоөткізгіштік математикалық моделі
- •33. Ньютондық емес сұйықтың тұтқырлықтары әртүрлі қозғалыстағы ағынға байланысты жылжымалы шекарасын модельдеу.
- •34. Ньютондық емес сұйықтың фильтірлену жылдамдығының сызбасы және механикалық мағанасы.
- •35. Сұйықтың негізгі модельдері.
- •36.Уақыт бойынша туындыларды айыру және механикалық мағанасы.
- •37.Скалярлық және векторлық шамалардың субстанциалық туындылары.
- •38.Үзіліссіздік теңдеудің механикалық мағанасы және моделін қорыту.
- •40.Қозғалыс мөлшерін математикалық модельдеу және механикалық мағанасы.
- •41.Қозғалыс мөлшерінің математикалық моделінің субстанциалдық тұрпатын модельдеу
- •41.Қозғалыс мөлшерінің математикалық моделінің субстанциалдық тұрпатын модельдеу.
- •42. Қозғалыс мөлшерінің математикалық моделінің субстанциалдық тұрпаты және механикалық мағанасы.
- •43.Ньютондық тұтқырлық заңының декарт координат жүйесіндегі формулалары.
1блок
15(1блок). Қозғалыс мөлшерінің теңдеуінен Пуассон теңдеуін қорыту
Тік бұрышты координат жүйесі үшін механикалық тұтас орта қозғалыс мөлшерінің теңдеуі
(∂ρv ⃗)/∂t=-[∇ρv ⃗v ⃗ ]-[∇τ ⃗ ]- ∇P+ρg ⃗
∂ρ/∂t+∇(ρv ⃗ )=0
Субстанциялық туындысы бойынша жазбасы
ρ (Dv ⃗)/Dt=[∇v ⃗ ]+∇P+ρg ⃗
Dρ/Dt+ρ(∇v ⃗ )=0
Бұл теңдеулердің көмегімен изотермиялық процесс (T=const) үшін , жүйедегі күй теңдеуін (ρ=ρ(P)) және тұтқырлықтың тығыздыққа (μ=μ(ρ) ) байланысын ескеріп осымен бірге жүйеге қойылатын шекаралық жіне бастапқы шарттары қойылған сұйықтың ағысы үшін қысым өрісін жылдамдықтардың таралуын табуға болады.
Жылдамдықтар бойынша аралас туындылар өзара тең болса және сұйықтың тұтқырлығы тұрақты μ=const болғандағы изотермиялық ағыс үшін Пуассонның теңдеуін қорытуға болады.Қозғалыс мөлшерінің ОХ өсі бойынша жылдамдықтарының құраушыларын жинақтап және Ньютондық жалпыланған тұтқырлық заңын ескріп Субстанциялық туындысы бойынша жазайық
ρ (Dv_x)/Dt=-∂P/∂x+∂/∂x [2μ (∂v_x)/∂x-2/3 μ(∇v ⃗ )]+∂/∂y [μ((∂v_x)/∂y+(∂v_y)/∂x)]+∂/∂z [μ((∂v_z)/∂x+(∂v_x)/∂z)]+ρg_x ;
Мұнда
2μ (∂v_x)/∂x=μ (∂v_x)/∂x+μ (∂v_x)/∂x
ескеріп
ρ (∂v_x)/∂t=-∂P/∂x-2/3 μ ∂/∂x (∇v ⃗ )+μ ∂/∂x ((∂v_x)/∂x)+μ ∂/∂x ((∂v_x)/∂x)+μ ∂/∂y ((∂v_x)/∂y)+μ ∂/∂y ((∂v_y)/∂x)+μ ∂/∂z ((∂v_z)/∂x)+μ ∂/∂z ((∂v_x)/∂z)+ρg_x
ρ (Dv_x)/Dt=-∂P/∂x-2/3 μ ∂/∂x (∇v ⃗ )+μ(∇∇) v_x+μ ∂/∂x ((∂v_x)/∂x+(∂v_y)/∂y+(∂v_z)/∂z)+ρg_x
Мұндағы
μ ∂/∂x ((∂v_x)/∂x+(∂v_y)/∂y+(∂v_z)/∂z)=μ ∂/∂x(∇v ⃗)
Топтастырып
-2/3 μ ∂/∂x (∇v ⃗ )+μ ∂/∂x (∇v ⃗ )=1/3 μ ∂/∂x(∇v ⃗)
Механикалық тұтас ортаның қозғалыс мөлшерінің Пуассон теңдеуін тік бұрышты координаталар жүйесі үшін толық жазайық.
ρ (Dv_x)/Dt=-∂P/∂x+μ/3 ∂/∂x (∇v ⃗ )+μ∇^2 v_x+ρg_x
ρ (Dv_y)/Dt=-∂P/∂y+μ/3 ∂/∂y (∇v ⃗ )+μ∇^2 v_y+ρg_y
ρ (Dv_z)/Dt=-∂P/∂z+μ/3 ∂/∂z (∇v ⃗ )+μ∇^2 v_z+ρg_z
Dρ/Dt=-ρ(∇v ⃗)
Пуассон теңдеуінің векторлық жазбасы
ρ (Dv ⃗)/Dt=-∇P+μ/3 ∇(∇v ⃗ )+μ∇^2+ρg ⃗
Dρ/Dt+ρ(∇v ⃗ )=0
ρ (Dv ⃗)/Dt=-gradP+μ/3 graddivv ⃗+divgradv ⃗+ρg ⃗
Dρ/Dt+ρdivv ⃗=0
1блок
1.Снарядтың ұшу траекториясын бірінші ретті дифференциалдық теңдеулер жүйесімен берілген Коши есебімен модельдеу.
Снарядтың траекториясын сипаттайтын модель алу
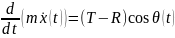
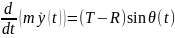 -mg
-mg
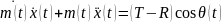
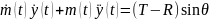 (t)-mg
(t)-mg
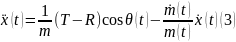
 (4)
(4)
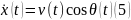
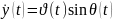 (6)
(6)
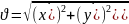 (7)
(7)
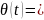 arctg
arctg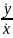 (8)
(8)
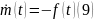
Бастапқы
шарттар: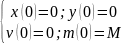 ,
,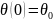
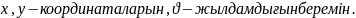
(6)теңдеулер жүйесіне берілетін бастапқы шарттар:
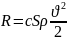
Зарядтың математикалық моделі
m=15
кг,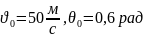 ,
,
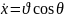
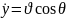
Осы теңдеулерден ІІ ретті туындысын аламыз.
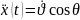 -
-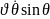
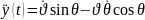
(3)теңдеуді (4)теңдеуге әкеліп қоямыз.Сонда
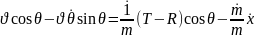
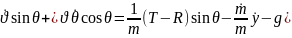
Жеңілдету үшін көбейтіп шығарамыз.
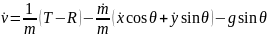
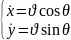 (12)
(12)
Соңғы
(12)теңдеуден
бірінші теңдеуді сos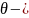 ға ,екіншісін sin
ға бөліп шықсақ,теңдеудің оң жағында
тек
ға ,екіншісін sin
ға бөліп шықсақ,теңдеудің оң жағында
тек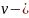 лар қалады.
лар қалады.
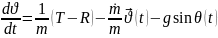 (11)
(11)
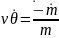 (
(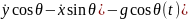
Ал
егер (12) теңдеудегі (1)- ші теңдеуді sin , (2)-ші теңдеуді cos
бөлсек,онда (13)- ші теңдеудегі
, (2)-ші теңдеуді cos
бөлсек,онда (13)- ші теңдеудегі
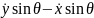 =0
=0
Ракетаның екінші ретті математикалық моделі( бірінші ретті дифференциалдық теңдеулер жүйесі)
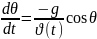 (13)
(13)
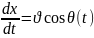 (14)
(14)
 (15)
(15)
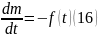
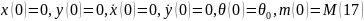
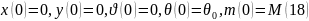
Қорытынды:
Т=0,m=15
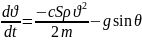 (19)
(19)
Бұрышқа байланысты теңдеуі:
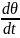 =-
=-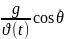 (20)
(20)
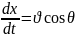 (21)
(21)
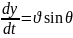 (22)
(22)
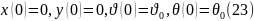
Снарядтың математикалық моделі.Бастапқы шарт.
M=constболса,T=0.
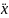 (t)=((-cρs
(t)=((-cρs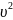 )/2*m)*cosθ
)/2*m)*cosθ
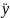 (t)=((-cρs
)/2*m)*sinθ*g
(5)
(t)=((-cρs
)/2*m)*sinθ*g
(5)
x(0)=0;y(0)=0;
θ(0)=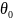 ,υ(0)=
,υ(0)=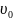 (7)-бастапқы
шарттары.
(7)-бастапқы
шарттары.
1-ші ретті теңдеуге келтіру:
( 8) жүйеге алып жаз пен :
(t)=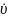 (t)cosθ(t)-υ(t)sinθ(t)
(t)cosθ(t)-υ(t)sinθ(t)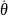 (t)
(t)
(t)= (t)sinθ(t)+υ(t)cosθ(t) (t)
(8)ден,(6)-ға,
жүйеге алып жаз: →
=((-cρs )/2*m)-gsinθ
=-gcosθ/υ
{→Бұл 1-ші ретті снарядтың дифференциалдық теңдеуі.
m=const
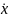 =υcosθ
=υcosθ
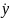 =υsinθ
=υsinθ
υ=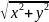
θ=arctg(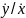 ),
x(0)=0;y(0)=0; θ(0)=
,υ(0)=
(7)-бастапқы
шарттары.
),
x(0)=0;y(0)=0; θ(0)=
,υ(0)=
(7)-бастапқы
шарттары.
2.Гармониялық тербелістің фазалық жазықтағы сипаттамасын математикалық модельдеу.
Гормоникалық осцилятор:
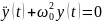
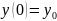
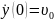
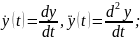
Дифференциалдық теңдеулердің автономдық жүйесі.
Сызықты дифференциалдық теңдеулердің қалыпты (нормальная система) жүйесі.
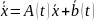
Мұнда
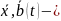 n
өлшемді
векторлар;
n
өлшемді
векторлар;
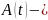 квадраттық
матрица;
квадраттық
матрица;
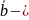 еркін мүше.
еркін мүше.
Анықтама
Тәуелсіз айнымалы шамалар айқын түрде кірмейтін жай дифференциалдық теңдеулер жүйесі автономдық делінеді.
Бұл дегеніміз теңдеулер жүйесінде қарастырылатын белгісіз функциялардың өзгеру заңдылығын уақыт өзгерісіне байланысты өзгермейді.
Автономдық жүйе:
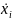 =
=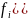 );
i=
);
i=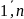
n – ретті автономдық қалыпты жүйе.
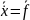 (
(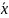 ),
),
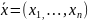 ,
,
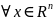 векторлық жазықтық.
векторлық жазықтық.
Автономдық қалыпты дифференциалдық n – жүйенің әрбір шешіміне қисық бойымен нүктенің қозғалысы сипатталады. Сөйтіп нүктелер бойынша алынған қисық фазалық траектория болады. Бұның кинематикалық интерпретациясы болады.
Ал шешімнің уақытқа байланысты сипаттамасы геометрикалық қисық болады.
Векторлық өріс кеңістіктің кез – келген нүктесінде күйдің (белгісіз функция) фазалық жылдамдығымен беріледі.
Фазалық кеңістікте эволюциялық процесті сипаттайтын функциялардың барлық мәндерінің жиыны беріледі.
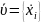 ,
i=
;
,
i=
;
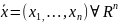
маятник теңдеуінің автономдық жүйесі:
Ауытқу
бұрышы:
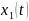 =y(t);
=y(t);
Бұрыштық
жылдамдық:
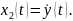
Жаңа (4) белгілеулер бойынша (1) теңдеуді екі теңдеуге бөлейік
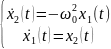 (5)
(5)
Фазалық кеңістік автономдық жүйенің векторлық өрістегі сипаттамасы.
(5) автономдық жүйе, вектор ...
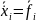 (
),
(
),
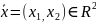 .
.
Сөйтіп (5) теңдеудің оң жағын нольге теңестіріп тепе – теңдік нүктесін табамыз. (координата системасының басы)
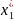 =
=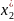 =0
(6)
=0
(6)
Векторлық өріс – фазалық жылдамдық:
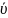 (
)=A
,
.
(7)
(
)=A
,
.
(7)
A – сызықтандыру матрицасы:
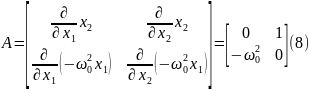
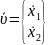 =
=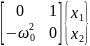 (
(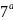 )
)
( ) векторлық өрісті сипаттайтын (5) векторлық
Фазалық
жазықтың
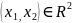 тепе – теңдік
=
=0
нүкте
тепе – теңдік
=
=0
нүкте
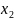
I I I
I I
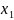 I:
I:
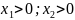
II:
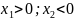
III:
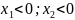
=
=0
IV:
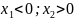
III IV
1 – сурет. Кинематикалық интерпретация. Өшпейтін тербеліс.
Интегралдық қисық тұйық
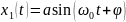
 (t)=
(t)=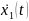 =
=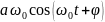
x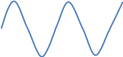
 (t)
(t)
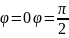
 t
t

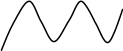
2 – сурет. Периодты тербеліс
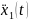 =
=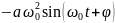 =
=