1.3.4. Таблицы сложения и умножения в двоичной системе счисления

Арифметические операции в двоичной системе счисления подобны соответствующим действиям в десятичной системе счисления, но при этом используются более простые таблицы арифметических действий.

В табл.2 приведены таблицы истинности для сложения и умножения в двоичной системы счисления.

Таблица 2 Таблица истинности для основных арифметических операций

Сложение				Умножение
a	b	перенос	a+b	a	b	ab
0	0	0	0	0	0	0
0	1	0	1	0	1	0
1	0	0	1	1	0	0
1	1	1	0	1	1	1

1.3.5. Перевод чисел из одной системы счисления в другую

Перевод чисел из десятичной системы счисления в другую систему и обратно связан с операциями ввода/вывода данных. Имеется несколько способов перевода чисел из одной системы в другую. Одним из часто используемых является метод деления числа на основание целевой системы счисления для целой части и умножения для дробной части исходного числа. Естественно, что деление и умножение чисел производится в исходной системе счисления.

Перевод целых чисел или целой части неправильной дроби.

Метод деления на основание целевой системы счисления.

Представим исходное число в виде полинома степени p, где p – основание целевой системы счисления, а – полином в целевой системе счисления:

1)

Искомое изображение величины находится как совокупность разрядных цифр: . 2)

Для нахождения (разряд за разрядом) разрядных цифр числа , разделим число в исходной системе счисления (равенство 1) на основание целевой системы счисления p. В результате этой операции получаем новое равенство:

3)

где:

• – частное от деления исходного числа на основание целевой системы счисления p,

• – остаток от деления исходного числа на основание целевой системы счисления p.

Из выражения 3 следует:

4)

и . 5)

Таким образом, младшая цифра числа в целевой системе счисления совпадает с остатком от деления числа на основание целевой системы счисления.

Значения остальных цифр числа (цифра за цифрой) можно найти, продолжая деление очередных частных на основание p. Деление продолжается, пока очередное частное не станет меньше основания целевой системы счисления.

Полученные цифры числа в новой системе счисления представлены в исходной системе счисления.

Если перевод производится в систему счисления с большим основанием, то требуется дополнительный перевод каждой цифры в целевую систему счисления.

Пример перевода десятичного числа 43_{(q = 10)} в двоичную систему счисления.

43	2
b0 = 1	21	2
	b1 = 1	10	2
		b2 = 0	5	2
			b3 = 1	2	2
				b4 = 0	1
					b5 = 1

Пример обратного перевода двоичного числа в десятичную систему счисления

Деление делается в двоичной системе счисления. Вначале основание целевой системы счисления 10 переводится в двоичную систему счисления:

Двоичное число делится на основание целевой системы счисления – . В результате деления получается частное – и остаток , равный младшей цифре числа в искомой системе счисления. Так как полученное частное – меньше основания (целевой системы счисления), то оно является старшей цифрой искомого кода.

Искомый код в двоично-десятичной системе приобретает вид: или, после перевода каждой цифры в десятичную систему счисления, – .

Перевод дробных чисел или дробной части неправильной дроби.

Метод последовательного умножения на основание системы счисления.

Представим исходную правильную дробь в виде полинома степени p, где p – основание, а – полином целевой системы счисления:

5)

Искомое изображение величины находится как совокупность разрядных цифр: . 6)

Для нахождения (разряд за разрядом) разрядных цифр числа , умножим число в исходной системе счисления (равенство 1) на основание целевой системы счисления p. В результате этой операции получаем неправильную дробь, в которой целая часть b_-1 p⁰ = b_-1 будет равна первой старшей цифре дроби в целевой системе счисления:

7),

где : -целая часть неправильной дроби и первая цифра дробной части числа в целевой системе счисления.

Продолжая эту операцию над дробной частью ( ) правой части равенства (7) можно цифра за цифрой вычислить значение последующих разрядов дроби.

Если перевод производится в систему счисления с большим основанием, то требуется отдельный перевод каждой цифры в целевую систему счисления.

Пример перевода правильной дроби в двоичную систему счисления.

Сдвиг переносов на 1 позицию	Умножение дробной части на основание – 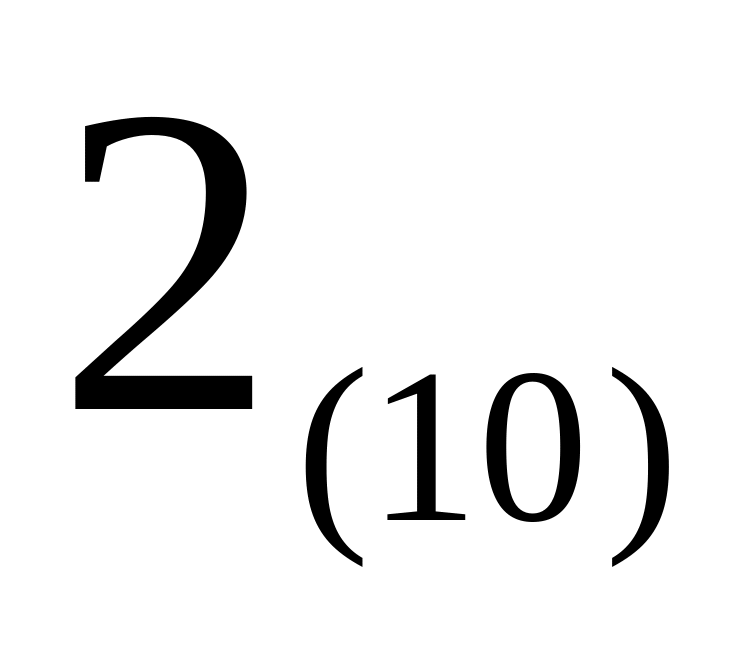. (Умножение производится в десятичной системе счисления.)
0,	,3125  2
0,0	,6250  2
0,01	,2500  2
0,010	,5000  2
0,0101	,0000  2
Результат

Пример перевода числа 0,0101(2) в десятичную систему счисления.
Сдвиг переносов на 4 позиции	Умножение дробной части на основание – 10(10) = 1010(2)
0,	,0101  1010 = 0011,0010
0,0011	,0010  1010 = 0001,0100
0,0011 0001	,0100  1010 = 0010,1000
0,0011 0001 0010	,1000  1010 = 0101,0000
0.0011 0001 0010 0101	,0000
Результат =

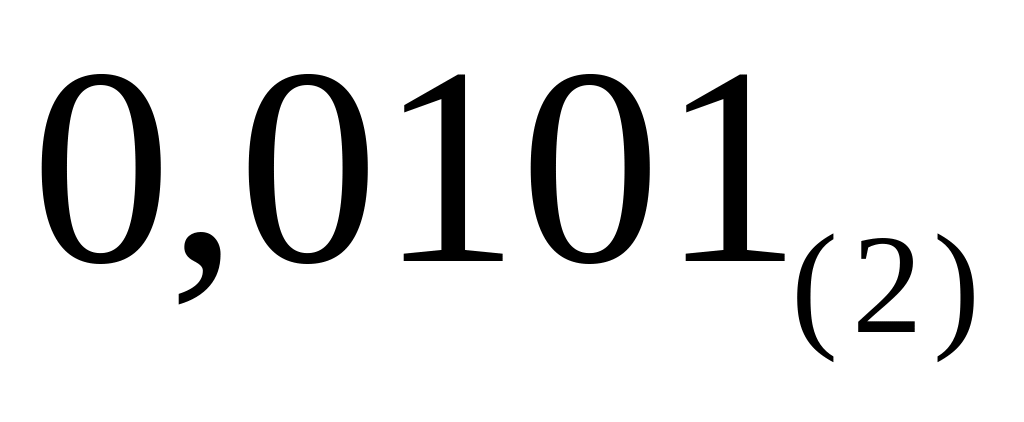В общем случае, дробные числа переводятся из одной системы счисления в другую приближенно, так как дробная часть числа при последовательном умножении на основание целевой системы счисления может не принимать значения нуля. В таких случаях перевод продолжается до достижения заданной точности. Примером может служить перевод числа 0,3₍₁₀₎ в двоичную систему счисления

Сдвиг переносов на 1 позицию	Умножение дробной части на основание – . (Умножение производится в десятичной системе счисления.)
0,	,3  2
0,0	,6  2
0,01	,2  2
0,010	,4  2
0,0100	,8  2
0,01001	,6  2 и т.д.
Результат

Рассмотренные выше методы перевода чисел из одной позиционной системы счисления в другую позиционную систему счисления являются классическими, но не единственными. На практике могут применяться и другие методы, например, метод подбора суммы убывающих степеней основания целевой системы счисления, равной по величине числу в исходной системы счисления. Например, число 138₍₁₀₎, может быть представлено в виде суммы степеней числа 2: 138₍₁₀₎ = 128₍₁₀₎ + 8₍₁₀₎ + 2₍₁₀₎ = 12⁽⁷⁾ + 02⁽⁶⁾ + 02⁽⁵⁾ + 02⁽⁴⁾ + 12⁽³⁾ + 02⁽²⁾ + 12⁽¹⁾ + 02⁽⁶⁾ = 10001010.