2.Пользовательские типы данных. Тип mpi_type_vector (hvector). Примеры
Чтобы построить тип данных для MPI, необходимо определить расположение данных в типе: тип элементов и их относительные местоположения в памяти. Такой тип называют производным типом данных.
Конструктор типа MPI_Type_vector создает тип, элемент которого представляет собой несколько равноудаленных друг от друга блоков из одинакового числа смежных элементов базового типа.
int MPI_Type_vector(int count, int blocklength, int stride, MPI_Datatype oldtype, MPI_Datatype *newtype)
count – число блоков; blocklength – число элементов базового типа в каждом блоке; stride – шаг между началами соседних блоков, измеренный числом элементов базового типа; oldtype – базовый тип данных; newtype – новый производный тип данных.
Функция создает тип newtype, элемент которого состоит из count блоков, каждый из которых содержит одинаковое число blocklength элементов типа oldtype. Шаг stride между началом блока и началом следующего блока всюду одинаков и кратен протяженности представления
базового типа.
Конструктор типа MPI_Type_hvector расширяет возможности конструктора MPI_Type_vector, позволяя задавать произвольный шаг между началами блоков в байтах.
int MPI_Type_hvector(int count, int blocklength, MPI_Aint stride, MPI_Datatype oldtype, MPI_Datatype *newtype)
count – число блоков; blocklength – число элементов базового типа в каждом блоке; stride – шаг между началами соседних блоков в байтах; oldtype – базовый тип данных; newtype – новый производный тип данных.
3. Напишите программу параллельного поиска минимального числа в массиве.
int main(int argc,char **argv)
{
int size,rank,i,n=12;
float a[]={10.0,-1.0,2.0,3.0,7.0,6.0,3.0,1.0,-2.0,4.0,-9.0,20.0};
MPI_Status status;
MPI_Init(&argc,&argv);
MPI_Comm_rank(MPI_COMM_WORLD,&rank);
MPI_Comm_size(MPI_COMM_WORLD,&size);
float f=0,min=0,mini=0;
int nachalo,konec,shag;
shag=n/(size-1);
if(rank!=size-1)
{
nachalo=rank*shag;
konec=rank*shag+shag;
min=a[nachalo];
for(i=nachalo;i<konec;i++)
if(a[i]<min)
min=a[i];
MPI_Send(&min,1,MPI_FLOAT,size-1,1,MPI_COMM_WORLD);
}
if(rank==size-1){
mini=32000;
for(i=0;i<size-1;i++)
{ MPI_Recv(&min,1,MPI_FLOAT,i,1,MPI_COMM_WORLD,&status);
if(mini>min)
mini=min; }
printf("%f\n",mini);
}
MPI_Finalize();}
72 Сурак
1. Закон Амдала с учетом сети. Ускорение. Эффективность.
Рассмотрим
некоторый последовательный алгоритм
решения какой-либо задачи. В нем есть
как операции, которые не могут выполняться
параллельно (например, ввод/вывод), так
и операции, которые можно выполнять на
нескольких процессорах одновременно.
Пусть доля последовательных операций
в алгоритме равна α. Время выполнения
последовательного алгоритма обозначим
T1. Время выполнения параллельной версии
алгоритма на p одинаковых процессорах
можно записать следующим образом:
(1)
Ускорением
параллельного алгоритма называют
отношение времени выполнения лучшего
последовательного алгоритмам к времени
выполнения параллельного алгоритма:
S=
(2)
Параллельный
алгоритм может давать большое ускорение,
но использовать для этого множество
процессов неэффективно. Для оценки
масштабируемости параллельного алгоритма
используется понятие ффективности: E=
(3)
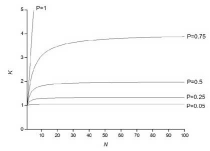
Теоретическую оценку максимального ускорения, достижимого для параллельного алгоритма с долей последовательных операций равной α определяется законом Амдала:
S=
=
(4)
Таким образом, если всего 10% операций алгоритма не может быть выполнена параллельно, то никакая параллельная реализация данного алгоритма не может дать больше ускорение более чем в 10 раз.
