II. Число (число Эйлера, число Непера)

Рассмотрим последовательность

Докажем, что эта последовательность имеет предел. Применим бином Ньютона

Если от перейти к , т.е. увеличить на единицу, то, прежде всего, добавится новый, -й полложительный член, каждый же из написанных членов увеличится, так как любой множитель в скобках вида заменится большим множителем . Отсюда и следует, что , т.е. последовательность возрастает.

Покажем, что она ограничена сверху. Опустив в выражении для все множители в скобках, мы этим увеличим его, так что

Заменив каждый множитель в знаменателях дробей числом , мы еще увеличим полученное выражение:

Но прогрессия, начинающаяся членом , имеет сумму меньше , поэтому .

Карл Теодор Вильгельм Вейерштрасс (1815–1897), будучи восемь лет преподавателем католической гимназии в городе Браунсберге, усиленно занимался математикой. Директор гимназии с уважением относился к его занятиям математикой. Однажды Вейерштрасс утром не явился на урок, дав ученикам повод пошуметь в классе. Директор гимназии, придя на квартиру к Вейерштрассу, к своему удивлению обнаружил, что он всю ночь занимался математикой и, не заметив наступившего уже утра, продолзжал свои размышления перед горящей лампой. Вскоре в знаменитом “Журнале чистой и прикладной математики”, издаваемом А.Л. Крелле (1780–1855), появилась статья Вейерштрасса по теории функций Абеля с датой 11 сентября 1853 года.

Много позднее сестра Вейерштрасса Клара в одном из писем Софье Владимировне Ковалевской (1850–1891) от 22 марта 1882 года писала: “Математики — самоистязатели”. Когда Карл одержим математикой, то даже “за едой он указательным пальцем правой руки пишет формулы на поверхности другой руки.”

Задачи.

1) Докажите, что данные последовательности имеют предл и найдите его:

1. 2. 3.

2) Докажите, что последовательность

не имеет предела.

3) выясните, при каких значениях последовательность :

имеет предел.

4) Найдите пределы последовательностей:

1.

2.

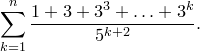
Второй замечательный предел

Обычно второй замечательный предел записывают в такой форме:

limx→∞(1+1x)x=e(1)

Число e, указанное в правой части равенства (1), является иррациональным. Приближённое значение этого числа таково: e≈2,718281828459045. Если сделать замену t=1x, то формулу (1) можно переписать в следующем виде:

limt→0(1+t)1t=e(2)

Как и для первого замечательного предела, неважно, какое выражение стоит вместо переменной x в формуле (1) или вместо переменной t в формуле (2). Главное – выполнение двух условий:

1. Основание степени (т.е., выражение в скобках формул (1) и (2)) должно стремиться к единице;

2. Показатель степени (т.е. x в формуле (1) или 1t в формуле (2)) должен стремиться к бесконечности.

Говорят, что второй замечательный предел раскрывает неопределенность 1∞. Заметьте, что в формуле (1) мы не уточняем, о какой именно бесконечности (+∞ или −∞) идёт речь. В любом из этих случаев формула (1) верна. В формуле (2) переменная t может стремиться к нулю как слева, так и справа.