
- •Степенная функция, ее свойства и график
- •Свойства синуса
- •Свойства косинуса
- •Свойства тангенса
- •Свойства котангенса
- •Производная степенной функции с произвольным показателем степени. Логарифмическое дифференцирование.
- •Производная показательной функции
- •Производные обратных тригонометрических функций
- •Примеры вычисления производных
- •Элементарные функции и их свойства Некоторые определения. Схема исследования
- •Определение и основные свойства предела последовательности
- •Предел монотонной ограниченной последовательности. Существование корня степени из вещественного числа. Число
- •II. Число (число Эйлера, число Непера)
- •Бесконечно большие и бесконечно малые последовательности
- •Связь между бесконечно малыми и бесконечно большими последовательностями
- •Оновные свойства бесконечно малых последовательностей
- •Свойства пределов функции
Производная показательной функции
Воспользуемся логарифмическим дифференцированием и получим производную показательной функции f (x) = ax. В соответствии с применяемым правилом, прологарифмируем правую и левую части по натуральному основанию
ln f(x) = ln ax = x·ln a,
дифференцируя правую и левую части этого равенства, получим
 ,
,
откуда найдём
f '(x) = ax·ln a,
В частном случае a = e производная показательной функции имеет более простой вид
![]() .
.
Производные обратных тригонометрических функций
Пусть f (x) = arctg x. По теореме о производной обратной функции имеем
 .
.

Пусть y = arcsin x. По теореме о производной обратной функции имеем
 .
.
Примеры вычисления производных
Пример 1. Вычислить производную функции
![]() .
.
Решение.
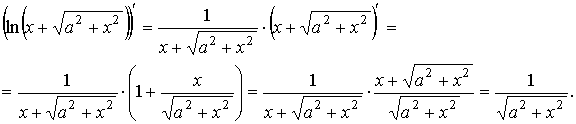 .
.

Пример 2. Вычислить производную функции y = earctg x. Решение. Данную функцию можно представить в виде y = eu, где u = arctg x. Тогда по правилу дифференцирования сложной функции имеем
 .
.
Заменяя u на arctg x, окончательно получим
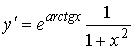 .
.
Пример 3. Вычислить производную функции
![]() .
.
Решение. Данную функцию можно представить в виде y = u2, где u = tg v, v = √ω, ω = x2 + 1. Используя правило вычисления производной сложной функции, получаем

Таблица производных простейших элементарных функций
(C)' = 0,
(x α) ' = α·x α-1 , в частности
 ,
(
,
( ,
,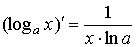 ,
в частности,
,
в частности,
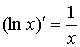 ,
,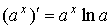 ,
в частности, (ex)' = ex,
,
в частности, (ex)' = ex,(sin x)' = cos x,
(cos x)' = − sin x,
 ,
,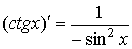 ,
, ,
,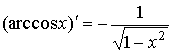 ,
,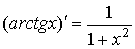 ,
,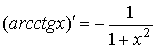 .
.
Формулы, приведенные в таблице, а также правила дифференцирования суммы, разности, произведения, частного и правило дифференцирования сложной функции являются основными формулами дифференциального исчисления. На основе правил и формул дифференцирования можно сделать важный вывод: производная любой элементарной функции также элементарная функция. Таким образом, операция дифференцирования не выводит из класса элементарных функций.
Элементарные функции и их свойства Некоторые определения. Схема исследования
Функцией (или функциональной зависимостью) называется закон, по которому каждому значению независимой переменной x из некоторого множества чисел, называемого областью определения функции, ставится в соответствие одно вполне определенное значение величины y. Совокупность значений, которые принимает зависимая переменная y, называется областью значений функции.
Графиком функции называется множество всех точек координатной плоскости с координатами (x;y), такими, что абсцисса x принимает все значения из области определения, а ордината y равна значению функции в точке x.
Функция f(x) называется четной, если для любого x из ее области определения, -x также принадлежит области определения, причем, f(-x)=f(x). Функция f(x) называется нечетной, если для любого x из ее области определения, -x также принадлежит области определения, причем, f(-x)=f(x).
Функция f(x) называется периодической с периодом T 0, если для любого x, принадлежащего области определения функции, x - T, x + T также принадлежат области определения и ее значения в точках x, x - T, x + T равны.
Функция f(x) возрастает на некотором интервале, если для любых значений x1 и x2, принадлежащих этому интервалу, таких что x2 > x1, выполнено неравенство f(x2) > f(x1).
Функция f(x) убывает на некотором интервале, если для любых значений x1 и x2, принадлежащих этому интервалу, таких что x2 > x1, выполнено неравенство f(x2) < f(x1).
Точка x0 называется точкой минимума функции f(x), если для всех значений x из некоторой окрестности x0 выполнено неравенство b R.
Точка x0 называется точкой максимума функции f(x), если для всех значений x из некоторой окрестности x0 выполнено неравенство f(x) f(x0).
При описании функции y = f(x) принято указывать:
1. Область определения D(x) и область значений E(y) функции.
2. Является ли функция периодической.
3. Является ли функция четной или нечетной.
4. Точки пересечения графика с осями координат.
5. Промежутки знакопостоянства функции.
6. Интервалы возрастания и убывания.
7. Точки экстремума и экстремальные значения.
8. Наличие асимптот.
9. График.
Возвратная последовательность, рекуррентная последовательность, последовательность a0, a1, a2,..., удовлетворяющая соотношению вида
ап+р + с1ап+р-1+... + срап = 0,
где с1,..., cp — постоянные. Это соотношение позволяет вычислить один за другим члены последовательности, если известны первые р членов. Классическим примером В. п. является последовательность Фибоначчи 1, 1, 2, 3, 5, 8,...(a0 = 1, a1 = 1,..., an+2 = an+1 + an). Возникновение термина «В. п.» связано с именем А. Муавра, который рассмотрел под названием возвратных рядов степенные ряды a0 + a1x + a2x2 +... с коэффициентами, образующими В. п. Такие ряды изображают всегда рациональные функции.
