
- •Степенная функция, ее свойства и график
- •Свойства синуса
- •Свойства косинуса
- •Свойства тангенса
- •Свойства котангенса
- •Производная степенной функции с произвольным показателем степени. Логарифмическое дифференцирование.
- •Производная показательной функции
- •Производные обратных тригонометрических функций
- •Примеры вычисления производных
- •Элементарные функции и их свойства Некоторые определения. Схема исследования
- •Определение и основные свойства предела последовательности
- •Предел монотонной ограниченной последовательности. Существование корня степени из вещественного числа. Число
- •II. Число (число Эйлера, число Непера)
- •Бесконечно большие и бесконечно малые последовательности
- •Связь между бесконечно малыми и бесконечно большими последовательностями
- •Оновные свойства бесконечно малых последовательностей
- •Свойства пределов функции
Понятие функции. Способы задания функции
Функцией
называется закон, по которому числу х
из заданного множества Х, поставлено в
соответствие только одно число у, пишут
![]() ,
при этом x называют аргументом функции,
y называют значением функции.
Существуют
разные способы задания функций.
1.
Аналитический способ.
Аналитический
способ - это наиболее часто встречающийся
способ задания функции.
Заключается
он в том, что функция задается формулой,
устанавливающей, какие операции нужно
произвести над х, чтобы найти у. Например
,
при этом x называют аргументом функции,
y называют значением функции.
Существуют
разные способы задания функций.
1.
Аналитический способ.
Аналитический
способ - это наиболее часто встречающийся
способ задания функции.
Заключается
он в том, что функция задается формулой,
устанавливающей, какие операции нужно
произвести над х, чтобы найти у. Например
![]() .
Рассмотрим
первый пример -
.
Рассмотрим
первый пример -
![]() .
Здесь значению x = 1 соответствует
.
Здесь значению x = 1 соответствует
![]() ,
значению x = 3 соответствует
,
значению x = 3 соответствует
![]() и
т. д.
Функция может быть задана на
разных частях множества X разными
функциями.
Например:
и
т. д.
Функция может быть задана на
разных частях множества X разными
функциями.
Например:
![]() Во
всех ранее приведенных примерах
аналитического способа задания, функция
была задана явно. То есть, справа стояла
переменная y, а справа формула от
переменной х. Однако, при аналитическом
способе задания, функция может быть
задана и неявно.
Например
Во
всех ранее приведенных примерах
аналитического способа задания, функция
была задана явно. То есть, справа стояла
переменная y, а справа формула от
переменной х. Однако, при аналитическом
способе задания, функция может быть
задана и неявно.
Например
![]() .
Здесь, если мы задаем переменной x
значение, то, чтобы найти значение
переменной у (значение функции), мы
должны решить уравнение. Например, для
первой заданной функции при х = 3, будем
решать уравнение:
.
Здесь, если мы задаем переменной x
значение, то, чтобы найти значение
переменной у (значение функции), мы
должны решить уравнение. Например, для
первой заданной функции при х = 3, будем
решать уравнение:
![]() .
То есть, значение функции при х = 3 равно
-4/3.
При аналитическом
способе задания, функция может быть
задана параметрически - это, когда х и
у выражены через некоторый параметр t.
Например,
.
То есть, значение функции при х = 3 равно
-4/3.
При аналитическом
способе задания, функция может быть
задана параметрически - это, когда х и
у выражены через некоторый параметр t.
Например,
![]() Здесь
при t = 2, x = 2, y = 4. То есть, значение функции
при х = 2 равно 4.
2. Графический
способ.
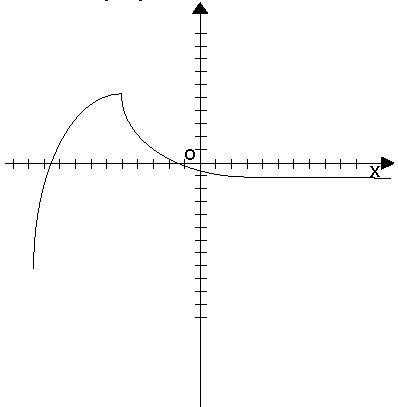
При графическом способе
вводится прямоугольная система координат
и в этой системе координат изображается
множество точек с координатами (x,y). При
этом
.
Пример:
Здесь
при t = 2, x = 2, y = 4. То есть, значение функции
при х = 2 равно 4.
2. Графический
способ.
При графическом способе
вводится прямоугольная система координат
и в этой системе координат изображается
множество точек с координатами (x,y). При
этом
.
Пример:
 3.
Словесный способ.
Функция задается
с помощью словесной формулировки.
Классический пример – функция
Дирихле.
«Функция равна 1, если х
– рациональное число; функция равна 0,
если х – иррациональное число».
4.
Табличный способ.
Табличный способ
наиболее удобен, когда множество Х
конечно. При этом способе составляется
таблица, в которой каждому элементу из
множества Х, ставится в соответствие
число Y.
Пример:
3.
Словесный способ.
Функция задается
с помощью словесной формулировки.
Классический пример – функция
Дирихле.
«Функция равна 1, если х
– рациональное число; функция равна 0,
если х – иррациональное число».
4.
Табличный способ.
Табличный способ
наиболее удобен, когда множество Х
конечно. При этом способе составляется
таблица, в которой каждому элементу из
множества Х, ставится в соответствие
число Y.
Пример:
 Табличный
способ задания функции очень удобен
при обработке результатов исследований.
Например, при выявлении зависимости
между уровнем загрязнения окружающей
среды и количеству людей, заболевших
раком.
Табличный
способ задания функции очень удобен
при обработке результатов исследований.
Например, при выявлении зависимости
между уровнем загрязнения окружающей
среды и количеству людей, заболевших
раком.
1. Понятие о сложной функции Пусть даны две функции z = f(y) и у = g(x). Сложной функцией (или композицией функций f и g) называется функция z = h(x), значения которой вычисляются по правилу h(x) = f(g(x)) (т. е. сначала вычисляется g(x), при этом получается некоторое число у, а затем вычисляется значение в точке у). |
Пример.
Функцию |
Для
записи композиции функций употребляется
значок
|
Пример.
Вычисляя
значения функции
,
необходимо брать только те числа х,
для которых
|
2. Взаимно обратные функции Пусть дана функция у = f(x). Она имеет обратную, если из зависимости у = f(x) можно переменную х однозначно выразить через переменную у. Выразив х через у, мы получим равенство вида х = g(y). В этой записи g обозначает функцию, обратную к f. Если функция g является обратной для функции f, то и функция является обратной для функции g. Пару функций f и g называют взаимно обратными функциями. |
3. График обратной функции Если мы одновременно построим графики функций f и g в одной и той же системе координат, откладывая по оси абсцисс аргументы обеих функций, а по оси ординат – их значения, то эти графики будут симметричны друг другу относительно прямой у = х. |
4. Свойства взаимно обратных функций Отметим некоторые свойства взаимно обратных функций. 1) Тождества. Пусть f и g – взаимно обратные функции. Тогда : f(g(y)) = у и g(f(x)) = х. 2) Область определения. Пусть f и g – взаимно обратные функции. Область определения функции f совпадает с областью значений функции g, и наоборот, область значений функции f совпадает с областью определения функции g. 3) Монотонность. Если одна из взаимно обратных функций возрастает, то и другая возрастает. Аналогичное утверждение верно и для убывающих функций. 4) Графики. Графики взаимно обратных функций, построенные в одной и той же системе координат, симметричны друг другу относительно прямой у = х. |
Степенная функция, ее свойства и график
Вы знакомы с функциями y=x, y=x2, y=x3, y=1/x и т. д. Все эти функции являются частными случаями степенной функции, т. е. функции y=xp, где p - заданное действительное число. Свойства и график степенной функции существенно зависит от свойств степени с действительным показателем, и в частности от того, при каких значениях x и p имеет смысл степень xp. Перейдем к подобному рассмотрению различных случаев в зависимости от показателя степени p.
Показатель p=2n -четное натуральное число.
В этом случае степенная функция y=x2n, где n - натуральное число, обладает следующими
свойствами:
область определения - все действительные числа, т. е. множество R;
множество значений - неотрицательные числа, т. е. y больше или равно 0;
функция y=x2n четная, так как x2n=(-x)2n
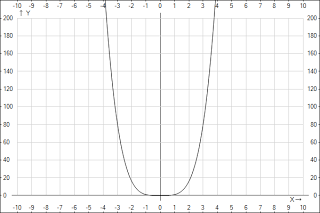
функция является убывающей на промежутке x<0 и возрастающей на промежуткеx>0. График функции y=x2n имеет такой же вид, как например график функции y=x4.
2. Показатель p=2n-1- нечетное натуральное число В этом случае степенная функция y=x2n-1 , где натуральное число, обладает следующими свойствами:
область определения - множество R;
множество значений - множество R;
функция y=x2n-1 нечетная, так как (-x)2n-1=x2n-1;
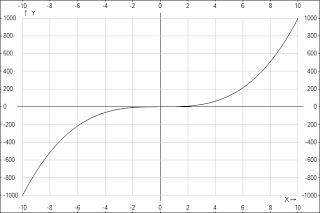
функция является возрастающей на всей действительной оси. График функции y=x2n-1 имеет такой же вид, как, например, график функции y=x3.
3.Показатель p=-2n, где n - натуральное число. В этом случае степенная функция y=x-2n=1/x2n обладает следующими свойствами:
область определения - множество R, кроме x=0;
множество значений - положительные числа y>0;
функция y=1/x2n четная, так как 1/(-x)2n=1/x2n;
функция является возрастающей на промежутке x<0 и убывающей на промежутке x>0.
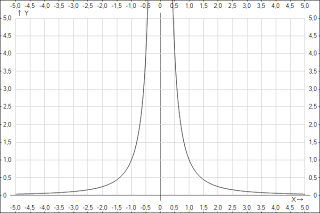
График функции y=1/x2n имеет такой же вид, как, например, график функции y=1/x2.
4.Показатель p=-(2n-1), где n - натуральное число. В этом случае степенная функция y=x-(2n-1) обладает следующими свойствами:
область определения - множество R, кроме x=0;
множество значений - множество R, кроме y=0;
функция y=x-(2n-1) нечетная, так как (-x)-(2n-1) =-x-(2n-1);
функция является убывающей на промежутках x<0 и x>0.
График функции y=x-(2n-1) имеет такой же вид, как, например, график функции y=1/x3.
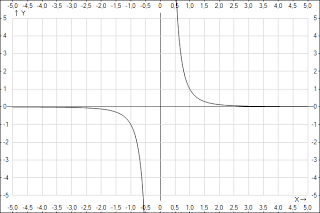
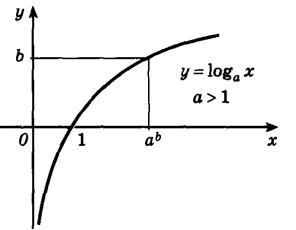
Основные свойства логарифмической функции:
1. Областью определения логарифмической функции будет являться все множество положительных вещественных чисел. Для краткости его еще обозначают R+. Очевидное свойство, так как каждое положительное число имеет логарифм по основанию а.
2. Областью значения логарифмической функции будет являться все множество вещественных чисел.
3. Если основание логарифмической функции a>1, то на всей области определения функции возрастает. Если для основания логарифмической функции выполняется следующее неравенство 0<a
4. График логарифмической функции всегда проходит через точку (1;0).
5. Возрастающая логарифмическая функция, будет положительной при x>1, и отрицательной при 0<х<1.
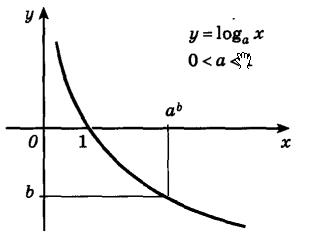
6. Убывающая логарифмическая функция, будет отрицательной при х>1, и положительной при 0<x<1:
На следующем рисунке представлен график убывающей логарифмической функции - (0<a<1):
7. Функция не является четной или нечетной. Логарифмическая функция – функция общего вид.
8. Функция не имеет точек максимума и минимума.
Если построить в одной оси координат показательную и логарифмическую функции с одинаковыми основаниями, то графики этих функций будут симметричны относительно прямой y = x. Данное утверждение показано на следующем рисунке.
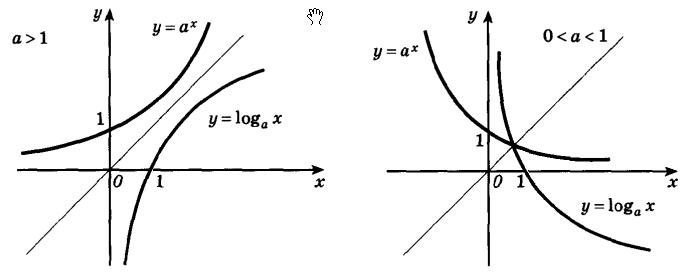
Изложенное выше утверждение будет справедливо, как для возрастающих, так и для убывающих логарифмических и показательных функций. Рассмотрим пример: найти область определения логарифмической функции f(x) = log8(4 - 5*x).
Исходя из свойств логарифмической функции, областью определения является все множество положительных вещественных чисел R+. Тогда заданная функция будет определена для таких х, при которых 4 - 5*x>0. Решаем это неравенство и получаем x<0.8.
Таким образом, получается, что областью определения функции f(x) = log8(4 - 5*x) будет являться промежуток (-∞;0.8)
