Министерство образования и науки РФ

Федеральное агентство по образованию

Саратовский государственный

технический университет

МАТЕМАТИЧЕСКИЕ МЕТОДЫ В ИНЖЕНЕРИИ

Методические указания

к изучению курса и выполнению контрольной работы

для студентов направления 657800

«Конструкторско-технологическое обеспечение

машиностроительных производств»

профиль «Технология машиностроения»

заочной формы обучения

Утверждено на заседании

Утверждено на заседании кафедры Протокол № от «14» октября 2011 г. Зав. кафедрой проф.Королев А.В.

Учебно-методической комиссии Протокол №1 от «14» октября 2011 г. Зав.УМК проф.Королев А.В.

2011 г.

Оглавление

Введение ……………………………………………………………………….3

1. Погрешность результата численного решения задачи 6

1.1 Причины возникновения и классификация погрешности 6

1.2 Прямая задача теории погрешностей 7

1.3 Обратная задача теории погрешности 7

Задачи контрольной работы по теме №1. 8

2. Аппроксимация и интерполирование функций 10

2.1 Общие понятия 10

2.2 Интерполяционный многочлен Лагранжа 10

2.3 Интерполяционная формула Ньютона. 11

2.4 Интерполяционные и экстраполяционные формулы при равноотстоящих значениях аргумента. 12

Формула Ньютона для интерполирования назад и экстраполирования вперед 13

2.5 Интерполяционные формулы Гаусса. 13

2.6 Задачи контрольной работы по теме №2 14

1. Найти приближенное значение функции f(x) по таблице значений этой функции: 14

3. Построение кривой по точкам 18

3.1 Общие понятия 18

3.2 Метод наименьших квадратов 18

3.2.1 Метод линеаризации данных по методу наименьших квадратов. 19

3.3 Интерполирование сплайнами 20

3.3.1 Кусочно-линейное и кусочно-квадратичное интерполирование 20

3.3.2 Простейший подход к сглаживанию 21

3.3.3 Кусочно-кубические сплайны 22

Задачи контрольной работы по теме №3 23

4. Приближенные вычисления определенных интегралов. 24

4.1 Интерполяционные квадратурные формулы 24

4.2 Квадратурные формулы Ньютона-Котеса. 24

4.2.1 Формула прямоугольников 25

4.2.2 Формула трапеций 25

4.2.3 Формула Симпсона (формула парабол) 25

4.3 Квадратурная формула Гаусса 26

4.4 Метод Монте-Карло 27

Задачи контрольной работы по теме №4 28

5. Вычисление собственных значений и собственных векторов матриц. 30

5.1 Метод Данилевского 30

5.2 Метод Крылова 32

5.3 Вычисление всех собственных значений положительно определенной симметрической матрицы 32

Задачи контрольной работы по теме №5 33

Литература 35

Введение Самостоятельная работа студентов заключается в изучении рекомендуемой литературы согласно разделам рабочей программы, решении типовых задач из сборника [19], выполнении контрольного задания и подготовке к практическим работам. Задачи и упражнения для аудиторной и самостоятельной работы студента обеспечивают закрепление лекционного материала и подготовку к выполнению контрольной и практическим работам.

Интегрированные системы для инженерных и научных расчетов Mathcad 6.0+ и Maple V, а также Maxima [6-10] должны использоваться для проверки правильности полученных результатов при выполнении контрольной работы, а также для решения задач на практических занятиях, требующих трудоемких вычислений. Данные системы представляют собой мощный инструмент, позволяющий автоматизировать наиболее рутинную и требующую повышенного внимания часть работы, оперирующий при этом аналитической записью данных, т. е. фактически математическими формулами. Система Maxima работает на тех же принципах и представляет похожий функционал, что и предыдущие; причем ее радикальным отличием является то, что она не является ни коммерческой, ни закрытой, а представляет собой свободное ПО. Именно с помощью этой системы рекомендуется выполнять задачи контрольной работы.

Студенту необходимо выполнить контрольную работу, состоящую из пяти задач. Контрольную работу выполняют и представляют на рецензию в форме пояснительной записки (ПЗ) объемом, как правило, 12-15 страниц текста, включая схемы, рисунки и таблицы. Пояснительная записка пишется через 1,5 интервала на листах формата А4 (210×297 мм).

Текст записки делят на разделы в соответствии с рассматриваемыми вопросами (темами). Разделы нумеруют арабскими цифрами. Введение не нумеруют. После номера раздела ставят точку. После названия раздела, точку не ставят. Текст раздела можно разделять на подразделы, которые нумеруют арабскими цифрами в пределах каждого раздела. Номер подраздела должен включать номер раздела и номер подраздела, разделенные точкой (например «2.3.», «3.1.» и т.п. ). В заголовках разделов и подразделов не должно быть переносов слов. Заголовки подразделов следует писать, отступив две строки от предыдущего текста. Отступив строку после заголовка, начинают писать текст подраздела. По всему тексту ПЗ следует собрать единство терминологии. Размерность одного и того же параметра в пределах ПЗ должна быть постоянной.

Математические формулы должны быть написаны отчетливо. В экспликациях значения символов и числовых коэффициентов приводят непосредственно под формулой с указанием размерности и в той последовательности, в какой они даны в формуле. Первую строку экспликации начинают со слова «где», двоеточие после которого не ставят.

Иллюстрации в записке (рисунки, схемы, чертежи и т.п.) и таблицы располагают по тексту ПЗ после первого упоминания о них, снабжают пояснительными надписями и номерами, на которые делают ссылки в тексте пояснительной записки. Рисунки нумеруют последовательно арабскими цифрами порядковой нумерации в пределах всей ПЗ.

Все иллюстрации именуют рисунками (сокращенно «Рис.»). Каждый рисунок сопровождают содержательной надписью, которую располагают под рисунком после его номера. Здесь же дают расшифровку условных обозначений, принятых на рисунке. Допускается выполнение рисунков на отдельной странице.

Каждая таблица должна иметь заголовок, поясняющий сущность материала, представленного в таблице. Заголовок помещают над таблицей и начинают с прописной буквы. Таблицы нумеруют последовательно арабскими цифрами порядковой нумерации в пределах всей ПЗ. Номер таблицы размещают перед ее заголовком.

Нумерация страниц записки должна быть сквозной: первой страницей является титульный лист, второй – содержание, третьей – введение и т.д. Номер проставляют, начиная со второй страницы, арабскими цифрами в правом верхнем углу.

Все ссылки на использованные литературные источники дают по тексту ПЗ в квадратных скобках с указанием номера по списку использованной литературы (например [2], [5], и т.п.).

Список использованных литературных источников включают в сквозную нумерацию страниц и оформляют в соответствии с общепринятыми правилами.

При выборе варианта контрольной работы следует помнить, что номер варианта соответствует последней цифре номера зачетной книжки студента.

1.Погрешность результата численного решения задачи

1.1Причины возникновения и классификация погрешности

Отклонение истинного решения от приближенного назовем погрешностью.

Решение задач всегда имеют погрешность, связанную со следующими причинами:

1) созданием математической модели (любая модель имеет свою степень точности);

2) получением исходных данных (т.к. являются "результатом измерений", следовательно, возникают измерительные погрешности);

3)использованием вычислительной техники (ошибки округления, возникающие из-за ограниченной разрядной сетки и ошибки, связанные с самими методами. На рис. 1 и 2 показаны составляющие неустранимой и полной погрешности.

Рис. 1. Cоставляющие неустранимой погрешности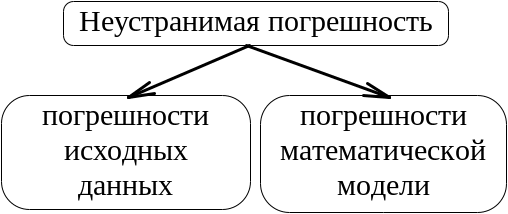

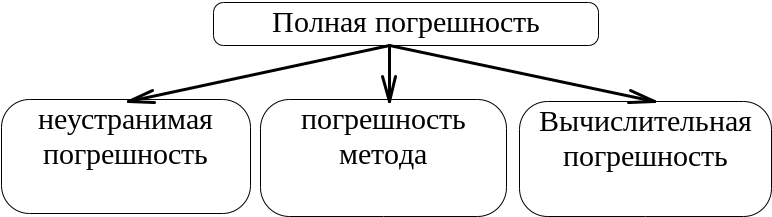
Рис. 2. составляющие полной погрешности

Неустранимую погрешность и погрешность метода необходимо контролировать, чтобы не осуществлять расчеты с избыточной точностью.

Характеристиками точности результата решения задачи являются абсолютная и относительная погрешности. Для технических задач 10 % - хорошая точность.

Определение. Если х - точное значение некоторого числа, х^* - приближенное, то абсолютной погрешностью приближения х^* назовем величину: , т.е. точное значение числа х заключено в границах .

Определение. Отношение абсолютной погрешности к абсолютному значению приближенной величины есть относительная погрешность (т.е. доля истинного значения): , при условии, что .

Пример: Найти абсолютную и относительную погрешности, если х=3.141592, а х^*=3.14.

Решение: .

Определение. Значащими цифрами числа называются все цифры в его записи, начиная с первой ненулевой слева.

Пример: У чисел подчеркнуты значащие цифры: 0.010087 и 0.0100870000.

Любое число можно представить в виде , где b - основание системы счисления, n – некоторое целое число (старший десятичный разряд числа х), а_i – значащие цифры приближенного числа x.

Определение. Значащая цифра а_k считается верной, если имеет место неравенство: , где , в противном случае а_k - сомнительная цифра.

1.2Прямая задача теории погрешностей

Основная задача теории погрешностей заключается в следующем: по известным погрешностям некоторой системы параметров требуется определить погрешность функции от этих параметров.

Пусть задана дифференцируемая функция у=f(х₁, х₂,¼,х_n) и пусть - абсолютные погрешности аргументов. Тогда абсолютная погрешность функции: (формула Лагранжа).

Заметим, что при замене полного приращения полным дифференциалом получаем аналогичное соотношение.

При зависимости функции от одного параметра .

Определение. Предельной абсолютной погрешностью называют следующую оценку погрешности величины у^*, т.е. .

Пусть задана дифференцируемая функция у=f(х₁, х₂,¼,х_n) и пусть - относительные погрешности аргументов. Тогда относительная погрешность: или .

Определение. Предельной относительной погрешностью называю величину .

Относительная погрешность суммы

. Пусть , а . Следовательно

Замечание: на практике применяется верхняя оценка.

Правила вычисления погрешностей [1]:

1. Предельная абсолютная погрешность суммы или разности равна сумме предельных погрешностей.

2. Относительная погрешность суммы положительных слагаемых не превышает наибольшей из относительных погрешностей этих слагаемых.

3. Предельная относительная погрешность произведения или частного равна сумме предельных относительных погрешностей.

4. Предельная относительная погрешность степени и корня приближенного числа равна произведению предельной относительной погрешности этого числа на показатель степени.