5.4 Тема №4
Дифференцирование
Задание 4.1.7. Найти производные функций.
Решение:
а)
б)
в)
г)
Задание № 4.3.7. Найти предел функции с помощью правила Лопиталя или эквивалентных бесконечно малых.
Решение о выборе метода принять самостоятельно.
Решение:
5.5 Тема №5
Исследование функций
Задание 5.1
Найти наибольшее и наименьшее значения
функции
на отрезке
.
Решение:
Найдём производную данной функции:
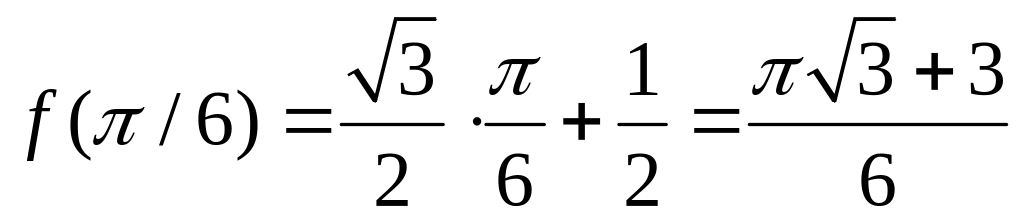- наибольшее
значение;
- наименьшее
значение.
Задание 5.2.7. Исследовать методами дифференциального исчисления функции и построить их графики.
Решение:
Область определения:
Так как
, то
- вертикальная асимптота.
Проверим наличие
наклонных и вертикальных асимптот,
которые будем искать в виде у = kx
+ b,
где k
и b
будем искать по следующим формулам.
Следовательно, у = 4- горизонтальная асимптота.
Точка (0,0) – точка пересечения с осями координат.
Найдём первую производную:
График функции
убывает на
Точек экстремума нет.
Найдём вторую производную:
-
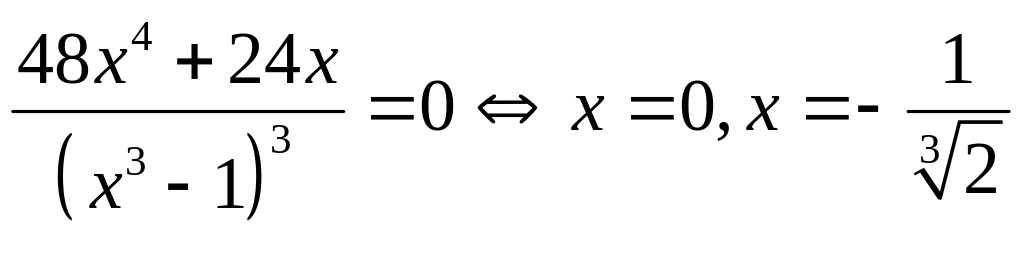
+ 0 - 1 +
Функция выпуклая
на интервале
и вогнутая на
.
Х= и х = 0 - точки перегиба.
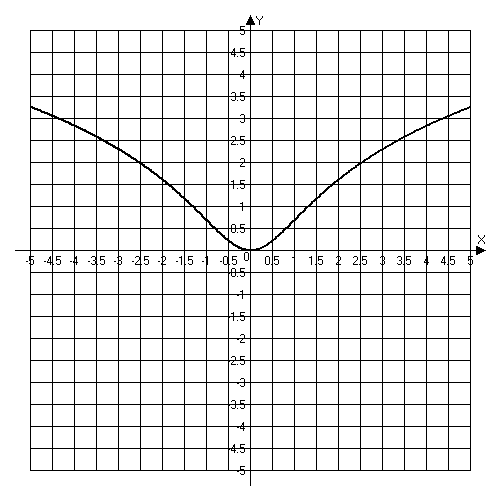
Выполним построение:
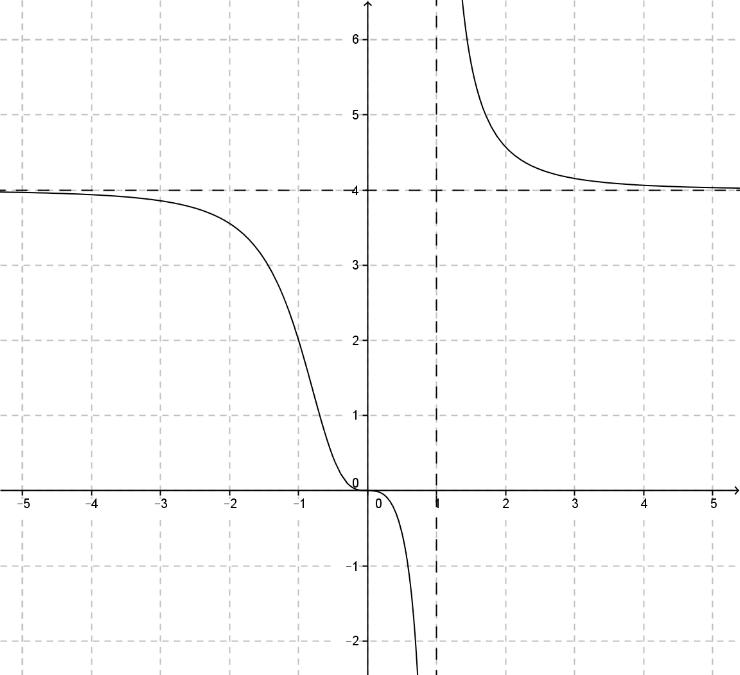
Решение
1. Область определения
функции:
,
так как
для любых х.
2. Четность-нечетность.
Функция является четной, значит, её график симметричен относительно оси ординат.
3. Вертикальных асимптот нет, так как функция непрерывна.
Исследуем функцию на наличие наклонных и горизонтальных асимптот.
Y = kx +b
,
Значит, асимптот нет.
4. Найдём первую производную:
- +
0 х
Функция убывает
на (-
;
0) и возрастает на (0;+
).
Точка х= 0 – точка минимума.
5. Найдём вторую производную:
-
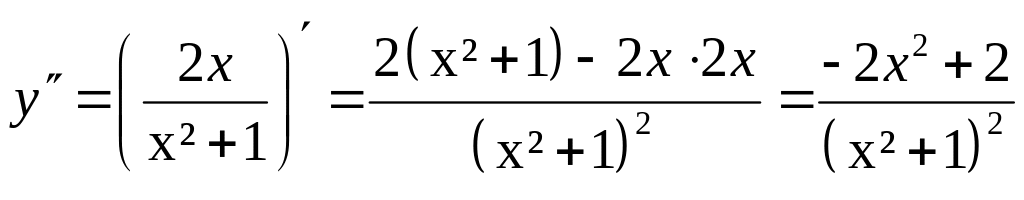
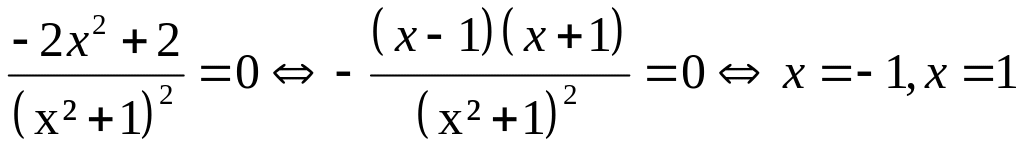
-1 + 1 -
Функция выпуклая на интервалах (- , -1) и (1,+ ) и вогнутая вниз на (-1,1)
Х = -1 и х = 1 – точки перегиба.
6. Дополнительные точки:
х |
0 |
-1 |
1 |
у |
0 |
|
|
Построим график:
