Вариант 7 Контрольная работа № 1
Линейная алгебра
Задание 1.1.7. Вычислить определитель матрицы С.
Решение:
Задание 1.2.7. Решить систему линейных уравнений
методом Крамера;
методом Гаусса.
Решение:
Методом Крамера.
Вычисляем определитель системы:
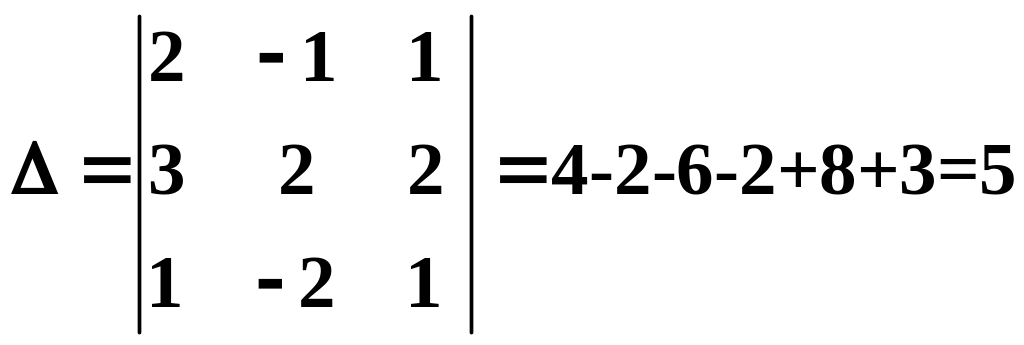
так как определитель
системы
,
следовательно, система имеет решение
и при этом одно.
Вычисляем остальные определители:
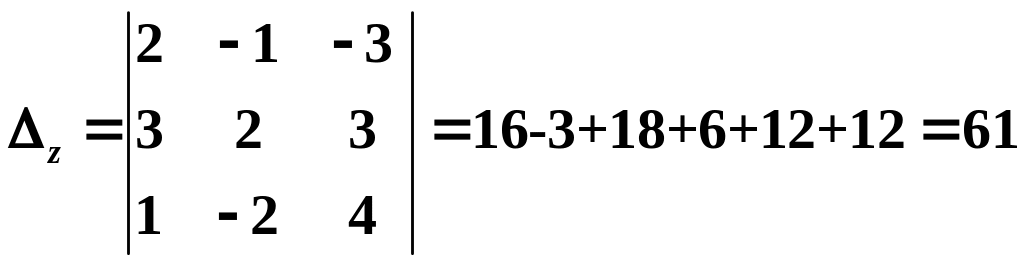
Вычисляем значения неизвестных по формулам Крамера:
;
;
.
Метод Гаусса.
|
2 |
-1 |
1 |
-3 |
|
3 |
2 |
2 |
3 |
||
1 |
-2 |
1 |
4 |
1-ую строку делим на 2
|
1 |
-0.5 |
0.5 |
-1.5 |
|
3 |
2 |
2 |
3 |
||
1 |
-2 |
1 |
4 |
от 2; 3 строк отнимаем 1 строку, умноженную соответственно на 3; 1
|
1 |
-0.5 |
0.5 |
-1.5 |
|
0 |
3.5 |
0.5 |
7.5 |
||
0 |
-1.5 |
0.5 |
5.5 |
2-ую строку делим на 3.5
|
1 |
-0.5 |
0.5 |
-1.5 |
|
0 |
1 |
1/7 |
15/7 |
||
0 |
-1.5 |
0.5 |
5.5 |
от 1; 3 строк отнимаем 2 строку, умноженную соответственно на -0.5; -1.5
|
1 |
0 |
4/7 |
-3/7 |
|
0 |
1 |
1/7 |
15/7 |
||
0 |
0 |
5/7 |
61/7 |
3-ую строку делим на 5/7
|
1 |
0 |
4/7 |
-3/7 |
|
0 |
1 |
1/7 |
15/7 |
||
0 |
0 |
1 |
12.2 |
от 1; 2 строк отнимаем 3 строку, умноженную соответственно на 4/7; 1/7
|
1 |
0 |
0 |
-7.4 |
|
0 |
1 |
0 |
0.4 |
||
0 |
0 |
1 |
12.2 |
Решение системы:
|
x = -7.4 |
у = 0.4 |
|
z = 12.2 |
Задание 1.3.7. Решить систему методом Гаусса или доказать, что она несовместна. Если система имеет бесчисленное множество решений, найти общее и одно частное решения.
Решение:
Перепишем систему уравнений в матричном виде и решим её методом Гаусса
|
2 |
1 |
5 |
-3 |
-2 |
|
1 |
-2 |
-3 |
2 |
5 |
||
3 |
-1 |
2 |
-1 |
3 |
||
|
|
|
|
|
1-ую строку делим на 2
|
1 |
0.5 |
2.5 |
-1.5 |
-1 |
|
1 |
-2 |
-3 |
2 |
5 |
||
3 |
-1 |
2 |
-1 |
3 |
||
|
|
|
|
|
от 2; 3 строк отнимаем 1 строку, умноженную соответственно на 1; 3
|
1 |
0.5 |
2.5 |
-1.5 |
-1 |
|
0 |
-2.5 |
-5.5 |
3.5 |
6 |
||
0 |
-2.5 |
-5.5 |
3.5 |
6 |
||
|
|
|
|
|
2-ую строку делим на -2.5
|
1 |
0.5 |
2.5 |
-1.5 |
-1 |
|
0 |
1 |
2.2 |
-1.4 |
-2.4 |
||
0 |
-2.5 |
-5.5 |
3.5 |
6 |
||
|
|
|
|
|
от 1; 3 строк отнимаем 2 строку, умноженную соответственно на 0.5; -2.5
|
1 |
0 |
1.4 |
-0.8 |
0.2 |
|
|
0 |
1 |
2.2 |
-1.4 |
-2.4 |
|||
0 |
0 |
0 |
0 |
0 |
|||
|
|
|
|
|
|||
|
|
|
|||||
|
|
||||||
Перепишем систему:
|
x1 + 1.4x3 -0.8x4 = 0.2 |
x2 + 2.2x3 -1.4x4 = -2.4 |
Система имеет бесконечное множество решений
Полагая х3= С1 , х4 = С2 , получим общее решение:
Полагая х3=
х4
= 0, получим частное решение:
