5. Пересечение множеств. Свойства.

Пересечением множеств А и В называется множество, которое обозначают АВ и состоящее из всех тех элементов, что принадлежат одновременно множеству А и В: АВ = {х | хА и хВ}.

Непересекающимися называются множества А и В, не имеющие общих элементов: АВ = .

Из определения пересечения следует, что характеристическое свойство множества А В составляется из характеристических свойств пересекаемых множеств с помощью союза «и».

Найдем, например, пересечение множества А – четных натуральных чисел и множества В – двузначных чисел. Характеристическое свойство элементов множества А – «быть четным», а В – «быть двузначным числом». Тогда, согласно определению, элементы пересечения данных множеств должны обладать свойством «быть четным и быть двузначным числом». Полученное множество не пусто. Например, 26 А В.

Рассмотрим другой пример: найдем пересечение множеств

А ={1, 2, 3, 4, 5, 6, 7} и В = {2, 4, 6, 8, 10}: Образуем новое множество С, состоящее из общих элементов множеств А и В: С = А В = {2, 4, 6}.

На основе данного примера построим множество К, которое содержит все элементы множества А и множества В. Это новое множество выглядит так: К = {1, 2, 3, 4, 5, 6, 7, 8, 10}. Данное множество представляет собой объединение множеств А и В.

6. Объединение множеств. Свойства

Объедине́ние мно́жеств (тж. су́мма или соедине́ние) в теории множеств — это множество, содержащее в себе все элементы исходных множеств. Объединение двух множеств и обычно обозначается , но иногда можно встретить запись в виде суммы .

Объединение двух множеств

Объединение более чем двух множеств

Пусть дано семейство множеств Тогда его объединением называется множество, состоящее из всех элементов всех множеств семейства:

7. Разность множеств. Свойства.

Разность множеств А и В ( пишется А – В , рис.3 ) есть множество элементов, которые принадлежат множеству А , но не принадлежат множеству В. Это множество называется также дополнением множества В относительно множества А.

Симметричная разность множеств А и В ( пишется А \ В ) есть множество:

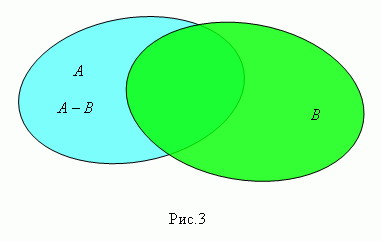
Разностью двух множеств А и В называют такое множество , в которое входят все элементы из А, не принадлежащие множеству В. При этом не предполагается, что множество В является частью множества А. Таким образом, при вычитании множества В из множества А из А удаляются пересечение А и В:

Например, если А – множество точек первого круга на рисунке 16, а В – множество точек второго круга, то и разностью является множество точек заштрихованной серповидной фигуры. При этом точки дуги MN удаляются из фигуры.

В случае, когда В – часть множества А, называют дополнением к В в множестве А и обозначают (разумеется, одно и то же множество В может иметь разные дополнения в разных содержащих его множествах А) (рис. 17). Например, дополнением множества четных чисел в множестве всех целых чисел является множество нечетных чисел. Дополнением множества всех квадратов в множестве прямоугольников является множество всех прямоугольников с неравными сторонами. А дополнением того же множества квадратов в множестве всех ромбов является множество ромбов с неравными смежными углами.