30. Задача о площади криволинейной трапеции, приводящая к понятию определенного интеграла. Геометрический смысл интеграла. Вычисление площади плоской фигуры с помощью определенного интеграла
Задача о площади криволинейной трапеции.
О: Под криволинейной трапецией
пониматся фигура
,
которая имеет границу
в данном случае
является
непрерывной (рис. 17.1).
Вычислим площадь криволинейной трапеции.
Для этого следует разделить отрезок
с
помощью точек
на
элементарных
отрезков
.
Отметим
определим
случайные точки
и
отобразим ступенчатую фигуру, состоящую
из прямоугольников с высотами
и
основаниями
.
Площадь ступенчатой фигуры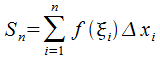
и
определяет приблизительное значение
площади криволинейной трапеции. В
качестве точного значения площади
запишем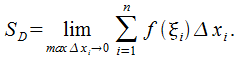
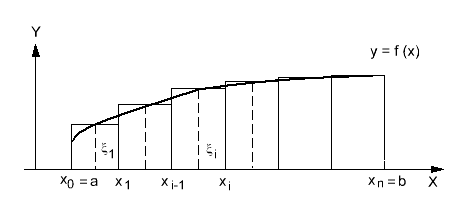Рис.
17.1
Геометрический
смысл определенного интеграла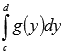 
состоит
в том, что его значение равно площади
криволинейной трапеции для непрерывной
и неотрицательной функции x=g(y)на
отрезке [c;d].
Также справедливо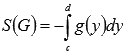 
для
непрерывной и неположительной
функции x=g(y) на
отрезке [c;d].
Вычисление площади плоской фигуры с помощью определенного интеграла в декартовой, полярной системах координат, в параметрическом случае.
-
Система координат
Площадь фигуры
1
Декартова
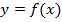
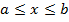
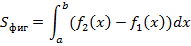
2
Параметрическая
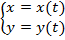
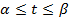
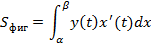
3
Полярная
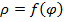
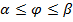
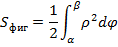
Пример:
Вычислить площадь фигуры, ограниченной
линиями 
, 
, 
.
31. Свойства определенного интеграла. Теорема Ньютона-Лейбница
Свойство 1. Производная от определённого интеграла по верхнему пределу равна подынтегральной функции, в которую вместо переменной интегрирования подставлено значение верхнего предела. То есть
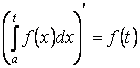
Свойство 2. Определённый интеграл от суммы функций равен сумме неопределённых интегралов
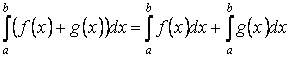
Свойство 3. Постоянный множитель можно выносить за знак определённого интеграла
Свойство
4. Если
на отрезке 
, где 
, функции 
и 
удовлетворяют условию 
, то
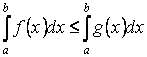
Свойство
5. Если
и 
- наименьшее и наибольшее значения
функции
на отрезке
и 
, то
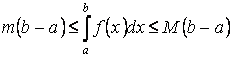
Свойство 6. Если поменять местами верхний и нижний пределы интегрирования, то определённый интеграл изменит знак
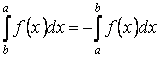
Свойство
7. Для
любых трёх чисел 
справедливо равенство
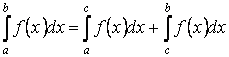
если
только все три интеграла существуют.
Свойство
8 (Теорема о среднем). Если
функция
непрерывна на отрезке
, то на этом отрезке найдётся такая
точка 
, что справедливо равенство:
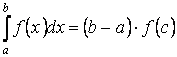
Ньютона-Лейбница теорема выражает
связь между определенным и неопределенным
интегралами от интегрируемой функции f(x):
если F(x) – любая первообразная
для функции f(x), то имеет
место формула Ньютона-Лейбница
.
Иногда
полезно применять эту теорему несколько
в иной форме, еще более ярко показывающей
связь операций интегрирования и
дифференцирования.
Если у = f(x)
– непрерывно дифференцируемая функция,
то
.
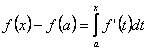Этот факт (наряду с другими элементами интегрального и дифференциального исчислений) был независимо открыт и И. Ньютоном, и Г. Лейбницем примерно в одно и то же время – в последней четверти XVII века.