14.Зарядталған бөлшектің градиенті өріс бойымен бағытталған магнит өрісіндегі қозғалысы

Декарттық координаттар жүйесін оның басында z осі магнит өрісіне параллель бағытталған болсын деп енгізейік. Онда . z осінің бағытын өзгертпей, координаттардың (R,φ,z) цилиндрлік жүйеге өтейік те, координат басының маңайындағы өлшемі ~ρ үлкен емес аймақты қарастырайық. 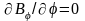шарт орындалса (өріске перпендикуляр бағыттағы градиентті елемеуге болса)

(1)

өрнектен

(2)

теңдеуді аламыз. Радиусы R= ρ дөңгелек ішінде

деп есептеуге болады, сондықтан (2) теңдеу интегралдауға келеді:

(3)

Егер бөлшек (R,φ) жазықтықта, z осінен R=ρ қашықтықта, жылдамдықпен қозғалса, оған z осі бағытында мынадай орташа күш әсер етеді:

, (4)

Импульс пен ρ үшін өрнектерді қолданып, (4) теңдеуді былай түрлендіруге болады:

. (5)

Бөлшек z осі бойымен қозғалған кезде, оның импульсінің р₁₁ құраушысы

(6)

жылдамдықпен өзгереді. Бұл өрнекті

(7)

түрде жазуға болады. Егер тек магнит күштер әсер етсе, онда тең энергия тұрақты болып қалады, демек

. (8)

(5) пен (8) өрнектерді (7) –ге қойып,

(9)

аламыз, мұнда d/dt туындысы сәйкесінші шаманың айналу центрінің магнит күш сызығы бойымен қозғалу нәтижесінде болатын өзгеруін білдіреді. (9)-дан

(10)

аламыз. Демек, бөлшектің айналыс центрінің күш сызықтар бойымен қозғалыс жүрісінде

(11)

шама тұрақты болып қалады.

Релятив емес жағдайда айналыс центрінің өріске параллель қозғалысының теңдеуін былай жазуға болады:

, (12)

бұл мына қатынасқа баламалы:

, (13)

мұндағы ,

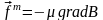ал (14)

15. Магнит айна

1-сурет.

Конфигурациясы суреттегідей магнит өрісіндегі бөлшектің қозғалысын қарастырамыз. Электр өрісі жоқ болған кезде формула былай жазылады:

,

, мұндағы α – бөлшектің питч бұрышы(бөлшектің жылдамдығы мен магнит индукциясы арасындағы бұрыш). В₀ – ең кіші өріс кезінде.

Магнит өрісінің мәні В₁ жеткен нүктеде бөлшек жылдамдығының магнит өрісіне параллель құраушы нолге айналады да, бөлшек кері бағытта қозғала бастайды. Яғни питч бұрышы аз емес зарядталған бөлшек күшейген магнит өрісі аймақтарынан шағылады.

Магнит айна-күшейген аймақ. 2 айна арасында бөлшек қақпанға түседі.

Егер бөлшектің питч бұрышы аз болса(α - В₁ ден аз болса), бөлшек қақпаннан шығып кетеді, себебі, В₀ –ді кіші мәнге бөлсек, В₁ үлкен мәнге ие болады, яғни қақпаннан шығады, бұл шығып кету конусы деп аталады.

* Егер жүргізуші центр B=B₁ нүктесіне жеткенде сонда v_ıı нольге айналады, яғни бөлшек әлсіз өріске қайта оралды дегенді білдіреді-шағылады. Сондықтан, кейде магнит күш сызықтарының бірігетін жерін магниттік айна деп атайды. Кеңістікте екі айнаның арасындағы(1-сурет) бөлшектің жылдамдық векторы мен өріс бағыты арасындағы α бұрышы белгілі мәннен асып кетеді де, екі шекарасынан да шағылады, сөйтіп, магнит өрісінде қармалады. Егер жылдамдық векторы мен өріс бағытының арасындағы бұрыш аз(кіші) болса, бөлшек айна арқылы өтіп кетеді. Осылайша, жылдамдықтар кеңістігінде шығып кету конусы немесе “жоғалту конусы” анықталды.

Қарастырып отырған типтің магниттік қармалуы Жердің магнит өрісіндегі орны дипольдің өрісіне ұқсас. Геомагниттік өрісте зарядталған бөлшектердің қармалуы арқасында Жерің радиациялы белдеуі бар.

Егер магниттік өріс уақыт бойынша өзгерсе, онда rot E нольге тең болмайды, және оның потенциалы болмайды. Сондықтан осы көрсетілген нәтижелер шынайы(дұрыс) болмайды. Бірақ, өріс бойымен қозғалатын орта магниттік күш бұл жағдайда да мына теңдеумен анықталады: сонда, dp_ıı/dt=- +eЕ‖‖

Магниттік айнаның қозғалуы сол қалпында калады, бірақта зарядталған бөлшек , бірақ енді зарядталған бөлшек құйынды электр өрістерімен(бетатрондық үдету) үдетіле алады, сондықтан бөлшектің кинетикалық энергиясы оның кеңістіктегі орналсуымен байланысты емес.

Егер бөлшек жақындатқыш магниттік айналардан көп шағылатын болса, онда оның энергиясы өседі.