3 Вопрос

Моментом силы относительно центра (обозначается m(F)) называется векторное произведение радиус-вектора r , проведенного из точки _O в точку приложения силы, на вектор силы _F

Момент силы относительно оси

 Моментом силы  относительно оси    (рис. 1.25), назы­вается алгебраиче­ская величина, абсолютное значение которой равняется произведению модуля проекции силы    на плоскость  , перпендикулярную к оси  , на расстояние    от точ­ки  пересечения оси с этой плоскостью до линии действия проекции силы на плоскость  , т.е.

  .З нак "плюс'' - если направление вращения силы    вокруг точки    с конца оси    видно происходящим против часовой стрелки, если по ча­совой стрелке, то знак "минус''. Очевидно, что момент силы относительно оси равен нулю, если линия действия силы и ось лежат в одной плоскости.

2 Вопрос

Проекция силы на ось и на плоскость.

Перейдем к рассмо­трению аналитического (численного) метода решения задач статики. Этот метод основывается на понятии о проекции силы на ось. Как и для всякого другого вектора, проекцией силы на ось называется скалярная величина, равная взятой с соответствующим знаком длине отрезка, заключенного между проекциями начала и конца силы. Проекция имеет знак плюс, если перемещение от ее начала к концу происходит в положительном направлении оси, и знак минус - если в отрицательном. Из определения следует, что проек­ции данной силы на любые параллельные и одинаково направлен­ные оси равны друг другу. Этим удобно пользоваться при вычисле­нии проекции силы на ось, не лежащую в одной плоскости с силой.

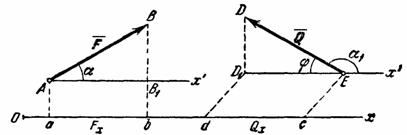
Рис. 12

 

Обозначать проекцию силы   на ось Ох будем символом  . Тогда для сил, изображенных на рис. 12, получим:

,     .

Но из чертежа видно, что  ,  .

Следовательно,

,  ,

т. е. проекция силы на ось равна произведению модуля силы на косинус угла между направлением силы и положительным на­правлением оси. При этом проекция будет положительной, если угол между направлением силы и положительным направлением оси - острый, и отрицательной, если этот угол - тупой; если сила перпен­дикулярна к оси, то ее проекция на ось равна нулю.

Рис.13    

Проекцией силы   на плоскость Оху называется вектор  , заключенный между проекциями начала и конца силы   на эту плоскость (рис. 13). Таким образом, в отличие от проекции силы на ось, проекция силы на плоскость есть величина векторная, так как она характеризуется не только своим чис­ленным значением, но и направлением в плоскости Оху. По модулю  , где   — угол между направ­лением силы   и ее проекции  .

В некоторых случаях для нахож­дения проекции силы на ось бывает удобнее найти сначала ее проекцию на плоскость, в которой эта ось ле­жит, а затем найденную проекцию на плоскость спроектировать на данную ось.                  Например, в случае, изображенном на рис. 13, найдем таким способом, что

1 Вопрос

Си́ла — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей. Приложенная кмассивному телу сила является причиной изменения его скорости или возникновения в нём деформаций и напряжений^[1][2].

Сила как векторная величина характеризуется модулем, направлением и «точкой» приложения силы. Последним параметром понятие о силе, как векторе в физике, отличается от понятия о векторе в векторной алгебре, где равные по модулю и направлению векторы, независимо от точки их приложения, считаются одним и тем же вектором . В физике эти векторы называются свободными векторами. В механике чрезвычайно распространено представление освязанных векторах, начало которых закреплено в определённой точке пространства или же может находиться на линии, продолжающей направление вектора (скользящие векторы)^[3].

Также используется понятие линия действия силы, обозначающее проходящую через точку приложения силы прямую, по которой направлена сила.

Второй закон Ньютона гласит, что в инерциальных системах отсчета ускорение материальной точки по направлению совпадает с равнодействующей всех сил, приложенных к телу, а по модулю прямо пропорционально модулю силы и обратно пропорционально массе материальной точки. Или, что эквивалентно, скорость изменения импульса материальной точки равна приложенной силе.

При приложении силы к телу конечных размеров в нём возникают механические напряжения, сопровождающиеся деформациями^[4][5][6][7].

С точки зрения Стандартной модели физики элементарных частиц фундаментальные взаимодействия (гравитационное, слабое, электромагнитное,сильное) осуществляются посредством обмена так называемыми калибровочными бозонами.^[4] Эксперименты по физике высоких энергий, проведённые в 70−80-х гг. XX в. подтвердили предположение о том, что слабое и электромагнитное взаимодействия являются проявлениями более фундаментального электрослабого взаимодействия^[8].

Размерность силы — LMT⁻², единицей измерения в Международной системе единиц (СИ) является ньютон (N, Н), в системе СГС — дина.

СЛОЖЕНИЕ СИЛ - нахождение геометрической суммы (т. н. главного вектора) данной системы сил путем последовательного применения правила параллелограмма сил или построения силового многоугольника. Для сил, приложенных в одной точке, при сложении сил определяется их равнодействующая.