
- •I. Связь ядра и внешних устройств:
- •II. Способ построения ядра:
- •Шестнадцатеричную) систему счисления.
- •Прямой, обратный, дополнительный коды.
- •Дополнительный код.
- •Логические функции.
- •Триггеры.
- •Регистры.
- •Приём и передача информации из регистра в регистр.
- •Запись информации в с одного регистра на другой регистр.
- •Дешифратор.
- •Сумматор.
- •Счётчики.
- •Принципы организации памяти эвм.
- •1 Этап. Выбор машинной команды.
- •1 Этап. Выбор машинной команды.
- •Способы адресации.
- •1. Прямая адресация.
- •2. Непосредственная адресация.
- •3. Косвенная адресация.
- •4. Регистровая адресация.
- •1 Этап. Выбор машинной команды.
- •1 Этап. Выбор машинной команды.
- •5. Базовая адресация.
- •6. Индексная адресация.
- •7. Базово-индексная адресация.
- •Микропрограмма выполнения двухадресной команды. Структура операционной части цп.
- •1 Этап. Выбор машинной команды.
- •8. Косвенно-регистровая адресация.
- •Организация алу
- •I Выполнение операций в алу для чисел с фиксированной точкой алу для выполнения операций сложения и вычитания над числами с фиксированной точкой.
- •Одноразрядный сумматор
- •Алу для выполнения операции умножения над числами с фиксированной точкой, представленных в прямом коде
- •1 Этап.
- •2 Этап.
- •Деление чисел с фиксированной точкой. Деление с восстановлением остатка и без.
- •1 Этап.
- •2 Этап.
- •3 Этап.
- •Структурная схема алу . (Для 2-ого случая).
- •Внешние прерывания
- •Организация в/в
- •Канальная команда
- •Сеанс начальной выборки
- •Сеанс связи по запросу ву
- •Магистральный ввод/вывод
- •Радиальный ввод/вывод
- •Микропроцессоры.
- •Intel 8086,8088
- •Intel 80286
- •1 Команда 2 команда
- •Intel 80386 dx
- •Intel 80386 sx
- •Intel 80486 dx
- •1.Многомашинные комплексы.
- •Видеорежимы.
Дополнительный код.
Дополнительным кодом целого двоичного числа называется число, образованное по формуле:
 0Xn-2
…
X1X0
,
X
0
0Xn-2
…
X1X0
,
X
0
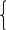 X=
X=
1Xn-2 … X1X0+1 , X 0
Дополнительный код дробного двоичного числа называется число, образованное по формуле:
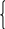 0,X-1
…
X-(n-1) ,
X=
0,X-1
…
X-(n-1) ,
X=
1,X-1 … X-(n-1)+2
X 0
, X 0
-(n-1)
Правило: Чтобы получить дополнительный код двоичного отрицательного числа необходимо в знаковый разряд поставить 1, все значащие разряды проинвертировать и к младшему разряду прибавить 1.
Это применимо как для целых так и для дробных чисел.
Пример:
А=5, В=4
1.1010 -5 обратный код 1.1011 -4 обратный код
+ 1 + 1
1.1011 -5 дополнительный код 1.1100 -4 дополнительный код
Для положительных чисел прямой и дополнительный коды совпадают.
Правило: Чтобы выполнить алгебраическое суммирование с использованием дополнительного кода, положительные числа представляются в прямом коде, отрицательные – в дополнительном, и производится суммирование кодов чисел включая знаковые разряды.
При возникновении 1 переноса из знакового разряда – она отбрасывается.
Если в знаковом разряде 1, значит результат отрицательный и представлен в дополнительном коде. Чтобы получить прямой код результата необходимо в знаковом разряде оставить 1, значащие разряды проинвертировать, к младшему разряду прибавить 1.
Пример:
А-В
1.1100 -4 дополнительный код
+0.0101 +5 прямой код

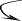 0.0001 +1
прямой
код
0.0001 +1
прямой
код
1
Если образовался “0” в знаковом разряде, то число получилось положительным и представлено в прямом коде, а если “1”, то это число отрицательное и представлено в дополнительном коде. Пример:
В-А
0.0100 +4 прямой код
+ 1.1011 -5 дополнительный код
1.1111
Знаковый разряд результата равен 1. Из этого следует, что результат получился отрицательным и представлен в дополнительном коде. Прямой код результата равен:
+ 1.0000
1
1.0001 -1 прямой код
Переполнение разрядной сетки.
Переполнением разрядной сетки называется ситуация, при которой результат требует на один разряд больше для своего представления, чем исходные операнды и результат не умещается в разрядную сетку.
В ЭВМ такая ситуация отслеживается блоком прерывания и в случае переполнения программа снимается с обработки.
Признаки переполнения(способы определения переполнения):
1) По наличию и отсутствию переноса в знаковый и из знакового разряда:
переполнение возникает в том случае, если возникает единица переноса в знаковый разряд и отсутствует единица переноса из знакового разряда. Либо имеется единица переноса из знакового разряда и отсутствует единица переноса в знаковый разряд.
Переполнение отсутствует, если существуют единицы переноса и в знаковый разряд и из знакового разряда или обе единицы переноса отсутствуют.
-
Пример:
А=5, В=4
0.101 +5 прямой код
0.100
+4 прямой код
1.010 -5 обратный код
1.011
-4 обратный код
 А+В
А+В
1
+
 0.101 +5
прямой
код
0.101 +5
прямой
код
+ 0.100 +4 прямой код
1.001 переполнение!
Имеется один перенос в знаковый разряд, перенос из знакового разряда отсутствует.
-А-В
 1
1
+1.010 -5 обратный код
1.011 -4 обратный код
0.101 переполнение!
Имеется один перенос из знакового разряда, перенос в знаковый разряд отсутствует.
2) Модифицированное кодирование:
При модифицированном кодировании под знак числа отводится два или более разрядов.
Комбинация 00 соответствует положительному числу. 11 – отрицательное число.
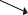
 10 переполнение
10 переполнение
01
Пример:
А+В
+ 00.101 +5 прямой модифицированный код
00.100 +4 прямой модифицированный код
01.001 переполнение!
Комбинация 01 в знаковом разряде соответствует переполнению разрядной сетки.
(-А)+(-В)
+11.010 -5 обратный модифицированный код
11.011 -4 обратный модифицированный код
10.101 переполнение!
Комбинация 10 в знаковом разряде соответствует переполнению разрядной сетки.
1
 Пример
для
дополнительного
модифицированного
кода:
Пример
для
дополнительного
модифицированного
кода:
А-В
00.101 +5 прямой модифицированный код
+11.100 -4 дополнительный модифицированный код
00.001 +1 прямой код
В знаковых разрядах результата комбинация 00.Из этого следует, что переполнение разрядной сетки отсутствует, результат положительный .
В-А
00.100 +4 прямой модифицированный код
+11.011 -5 дополнительный модифицированный код
11.111
В знаковых разрядах результата комбинация 11.Из этого следует, что переполнение разрядной сетки отсутствует и результат отрицательный ,представлен в дополнительном коде.
+ 11.000
1
11.001 -1 прямой код
(-А)+(-В)
+11.011 -5 дополнительный модифицированный код
11.100 - 4 дополнительный модифицированный код
10.111 переполнение!
В знаковых разрядах результата комбинация 10,что соответствует переполнению разрядной сетки.
Л4
Формы представления чисел в ЭВМ.
Любая информация(числа, команды и т.д.) представляются в ЭВМ в виде двоичных кодов фиксированной или переменной длины. Отдельные элементы двоичного кода, имеющие значение 0 или 1, называют разрядами или битами. В ЭВМ слова часто разбивают на части, называемые слогами или байтами. В современных ЭВМ широко используется байт, содержащий 8 бит(разрядов).
Двоичный разряд представляется в ЭВМ некоторым техническим устройством, например триггером, двум различным состояниям которого приписывают значения 0 и 1. Набор соответствующего количества таких устройств служит для представления многоразрядного двоичного числа(слова).
В ЭВМ применяют две формы представления чисел:
-с фиксированной точкой
-с плавающей точкой.
Форма представления чисел с фиксированной точкой.
При представлении чисел с фиксированной точкой положение точки фиксируется в
определённом месте относительно разрядов числа.
|
|
|
|
|
|
||
 знаковый
разряд n-1 возможное
положение
точки
знаковый
разряд n-1 возможное
положение
точки
0 – «+»
1 – «-»
1. Если точка фиксируется перед старшим разрядом числа, то число по модулю < 1.
2. Если точка фиксируется после младшего разряда числа, то число по модулю >
1.(только целые числа)
В современных ЭВМ для представления числе используется 2 способ.
Пример.
n=16 разрядов;
число «+5»;
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
В современных ЭВМ отрицательные числа хранятся
-в дополнительном коде;
-в обратном коде.
Дополнительный код -5:
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
Форма представления чисел с плавающей точкой.
Представление чисел с плавающей точкой в общем случае имеет вид:
px
x M x q
,где
Mx- мантисса,
Px- порядок числа,
q- основание системы исчисления.
Мантисса - нормализованная правильная дробь.
Нормализованная правильная дробь-первая цифра после точки(первая значащая цифра)
отлична от 0.
 Порядок
Px,
который
может
быть
положительным
или
отрицательным
числом,
определяет
положение
точки
в
числе
x.
Порядок
Px,
который
может
быть
положительным
или
отрицательным
числом,
определяет
положение
точки
в
числе
x.
Порядок отвечает за диапазон.
Мантисса отвечает за точность.
Арифметические действия над числами с плавающей точкой требуют выполнения помимо операций над мантиссами определённых операций над порядками(сравнение, вычитание и др.). Для упрощения операций над порядками их сводят к действиям над целыми положительными числами, применяя смещённый порядок Pсм.
L
Pсм Px
2 ,где L – число разрядов, отводимых под порядок.
L разрядов под порядок
………………………………
 …
…
знаковый знаковый разряд разряд числа порядка Px
0 – «+»
1 – «-»
Пример. n=32 разряда; L=6;
(22,35)10=(16,59…9)16
Mx=(0,1659…9)16; Px=2; L=6; Pсм=Px+2L=Px+(40)16=(42)16;
 7
7
мантисса числа
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
 1 6 5 9 9
1 6 5 9 9
смещённый порядок мантисса
Для отрицательных числе и мантисса и порядок всегда представляются в прямом коде,
кроме знака.
