34. Фотоэффект құбылысындағы Эйнштейннің теңдеуін эксперимент арқылы тексеру және Планк тұрақтысын анықтау.

Фотоэффекті түсіндіру үшін Эйнштейн мынадай ұйғарым жасады (1905ж.): жарық толқынының энергия ағыны үздіксіз емес, ол квант немесе фотон деп аталатын энергияның дискреттік үлестерінің ағыны болып табылады. Жиілігі ω жарыққа сәйкес келетін фотон энергиясы:

(1)

болады, мұндағы

Фотон металдағы электронмен соқтығысып, оған өзінің барлық энергиясын береді. Еркін электронмен соқтығысқан кезде оған фотонның барлық энергиясының берілуі мүмкін емес. Металдағы электр өткізгіштікті қамтамасыз ететін электрондар еркін электрондар деп аталады, бірақ олар өзара бірімен-бірі және кристалдық тордың басқа электр зарядтарымен әсерлеседі. Сондықтан олар динамикалық мағынада байланысқан электрондар болып табылады және фотонның бүкіл энергиясын толығынан жұта алады. Егер осы жұтылған энергия жеткілікті үлкен болса, онда электрон өзін металда ұстап тұратын күштерді жеңеді де металдан босап шыға алады. Әрине осы процесте энергияның сақталу заңы орындалады, оны мына түрде жазуға болады:

, (2)

мұндағы – электронның метал көлемінде ұстап тұратын күшті жеңіп және көлем аумағынан шыққан кездегі ең үлкен кинетикалық энергиясы; А – шығу жұмысы. (2) формула фотоэффект үшін Эйнштейн теңдеуі деп аталады. (2) теңдеуден фотон энергиясы электронның металдан шығу жұмысынан кем болған жағдайда фотоэффектің мүмкін еместігі көрінеді.

Планк тұрақтысы -  әсерлерінің сипаты үздікті болатын көптеген физикалық құбылыстарды анықтайтын түбегейлі физикалық тұрақты. Планк тұрақтысы   таңбасыменбелгіленеді. Бұл әмбебап тұрақтыны 1900 ж абсолюттық қара дененің сәуле шығару спектріндегі энергияның таралу заңдылықтарын зерттеу кезінде неміс физигі М.Планк енгізген. 

35.Диэлектриктен шағылған жарықтың поляризациялануын зерттеу.

Табиғи жарықтардың екі ортаның шекарасындағы шағылу және сыну кезінде, сынған және шағылған сәулелердің жарым жартылай поляризациялануы байқалатынын атап айтқан жөн. Бұл жарықтардың поляризациялану дәрежесі шағылатын бетке сәуленің түсу бұрышына тәуелді болады.

Белгілі диэлектрик үшін түсу бұрышының бір мәнінде шағылған жарық толығымен жазық поляризацияланады. Бұл жағдайда шағылған сәуле мен сынған сәуле арасындағы бұрыш 90⁰-қа тең болады, яғни түсу бұрышының тангенсі сол диэлектриктің сыну көрсеткішіне тең болады:

tgi_p = n (5.2)

(мұндағы n= n₂/n₁ - диэлектриктің салыстырмалы сыну көрсеткіші). Бұл (5.2) өрнекті Брюстер заңы деп атайды.

Осындай жағдайда шағылған сәуленің поляризацияланған жазықтығы сәуленің түсу жазықтығына перпендикуляр болады (5.2-сурет).

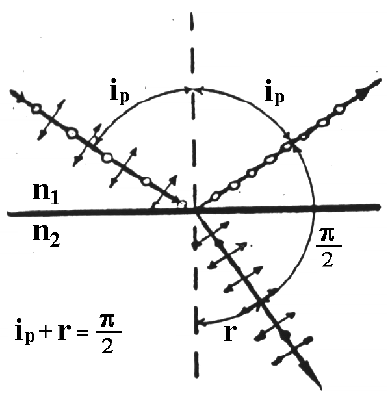
5.2-сурет. Брюстер заңын түсінуге арналған сурет

Жарықтың сынған сәулесі сәуленің түсу жазықтығында жарым-жартылай поляризация-ланған болады. Поляризация-лану дәрежесін мынадай қатынаспен анықтайды:

(5.3)

Екі ортаның шекарасына жазық поляризацияланған жарық түссе, Френельдің зерттеуі бойынша, диэлектриктің шағылдырғыш қабілеттілігі сәуленің түсу бұрышына және түскен сәуле ағынының поляризациясының сипаттамасына тәуелді болады:

(5.4)

(5.5)

Мұндағы ρ⊥ - түсу жазықтығына перпендикуляр жазықтықта поляризацияланған сәуленің шағылу қабілеттілігі; ρ || - түсу жазықтығына параллель жазықтықта поляризацияланған сәуленің шағылу қабілеттілігі; і және r сәуленің түсу және сыну бұрыштары (5.3 - суретке қараңыз).

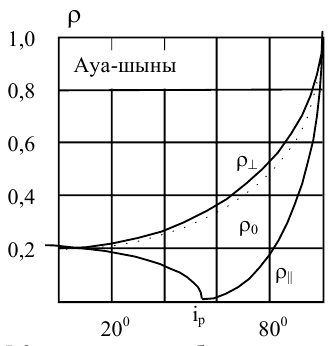
5.3-сурет.

n₁<n₂ болған кезде жарықтың шағылу коэффициенті түсу бұрышының функциясы болады.

Диэлектриктің шағылдыру қабілеттілігі – диэлектриктен шағылған жарық ағыны интенсивтігінің диэлектрикке түскен жарық ағынының ρ интенсивтілігіне қатнасымен 1,0 анықталатын салыстырмалы шама. Диэлектрик бетіне түскен поляризацияланбаған толқынның шағылу қабілеттілігі ρ₀ (5.4) және (5.5) өрнектер арқылы есептелініп анықталады, яғни поляризацияланбаған толқынды жазық-поляризацияланған ⊥ және || екі толқынға бөлу арқылы анықтайды. Бұл жағдайда

. (5.6)

5.3-суреттегіграфиктеншағылуқабілеттілігініңρ || еңминимуммәніполяризацияланғансәуленіңіp түсубұрышына, яғниБрюстершартынаншығатынбұрышқа (5.2 - сурет), сәйкескелетіндігінбайқауғаболады.