Аксиомы динамики

Динамикой называют раздел механики, в котором рассматривается движение материальных тел под действием приложенных к ним сил с учетом инерции. Инерцией называется свойство материального тела сохранять состояние движения или покоя при отсутствии действующих на тело сил. Физическую величину, зависящую от количества вещества и являющуюся мерой инерции тела в поступательном движении, называется массой тела m.

Основой динамики точки являются 4 аксиомы, изложенные ниже.

I аксиома (закон инерции): материальная точка (МТ), к которой не приложены силы, находится в состоянии покоя или равномерного прямолинейного движения, пока приложенные к ней силы не изменяют этого состояния. Движение МТ при отсутствии сил называют инерциальным. Систему отсчета (СО), в которой действует закон инерции, называют инерциальной СО. В большинстве задач СО, связанная с Землей, считается инерциальной.

II аксиома (основной закон динамики): ускорение МТ пропорционально приложенной к ней силе и направлено так же, как сила. Основное уравнение

.

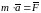III аксиома (закон о действии и противодействии): две МТ действуют друг на друга с равными по модулям силами, которые лежат на соединяющей эти точки прямой и направлены в противоположные стороны.

IV аксиома (закон независимости действия сил): геометрическая сумма ускорений, которые сообщаются МТ отдельно каждой приложенной к ней силой, равна ускорению, которое МТ получит под действием на нее всех сил.

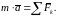
Вместо можно пользоваться уравнением , понимая под силой 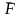равнодействующую.

Под действием на тело силы тяжести у тела возникает одно и то же ус­корение 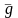, которое называют ускорением силы тяжести (ускорением свобод­ного падения). Если к МТ приложена только сила тяжести 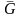, то по

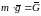. (4.1.3)

Масса тела не зависит от его местонахождения и от сил, приложенных к телу, а вес тела меняется с изменением ускорения силы тяжести в зависимости от географической широты места и расстояния от центра Земли.

Дифференциальные уравнения движения материальной точки

Рассмотрим движение МТ под действием сил {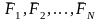 } относительно инерциальной СО Оxyz, считая, что среди сил имеются реакции связей.

Проецируя уравнение на естественные оси, получаем естественные дифференциальные уравнения движения (ДУД)

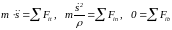; (4.1.4)

проецируя на декартовы оси, получаем ДУД точки в декартовых координатах

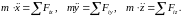(4.1.5)

ДУД применяются к решению двух основных задач динамики МТ:

1-я основная задача: по движению точки найти приложенную к ней силу. Здесь нужно продифференцировать уравнения движения МТ и результаты подставить в (4.1.4) или (4.1.5), откуда определяется приложенная к точке сила;

2-я основная задача: по силам, приложенным к точке, найти ее движение. Решая эту задачу, нужно в общем случае найти вторые интегралы дифференциальных уравнений (4.1.4) или (4.1.5). В частных случаях возможно интегрирование ДУД точки, применяя метод разделения переменных.

Билет16. Количество движения точки. Импульс силы. Теорема об изменении количества движения точки.

Законы динамики справедливы только в инерциальной СО. Рассмотрим движение МТ относительно СО, которая движется произвольно относительно инерциальной СО. Рассмотрим движение точки P под действием сил { }. В инерциальной СО справедливо основное уравнение динамики (4.1.2). Абсолютное ускорение точки можно найти по формуле (3.10.8)

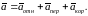(4.3.1)

Подставим (4.3.1) в равенство (4.1.5) и преобразуем его

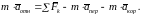(4.3.2)

Примем обозначения

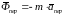(4.3.3)

и 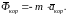(4.3.4)

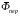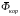Векторы и называют соответственно переносной и кориолисовой силами инерции.

Равенство (6.6) можно записать в виде

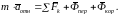(4.3.4)

Уравнение (4.3.4) называют основным уравнением динамики относительного движения МТ. Уравнения относительного движения МТ составляются также, как в случае абсолютного движения, если к числу действующих сил добавить переносную и кориолисову силы инерции. Наблюдатель, который находится в движущейся неинерциальной системе отсчета, воспринимает переносную и кориолисову силы инерции, как реально существующие силы. Но это неверно, так как в неинерциальной СО законы механики Ньютона не действуют, и рассматривать явления с точки зрения предыдущих аксиом нельзя.

Частные случаи основного уравнения относительного движения МТ:

а) при поступательном переносном движении

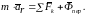(4.3.5)

б) при прямолинейном и равномерном переносном движении

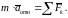(4.3.6)

Уравнения (4.3.6) и (4.1.2) совпадают, так как 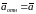. Следовательно, данная система отсчета инерциальная. Механическими опытами невозможно установить, неподвижна ли система отсчета, или она движется поступательно, равномерно и прямолинейно (принцип относительности Галилея);

в) в относительном состоянии покоя

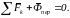(4.3.7)

Это уравнение относительного равновесия МТ.