
- •1. Предмет и методы физики взрыва и удара
- •1.1. Явление взрыва
- •1.2. Термодинамика взрывных процессов. Первый и второй законы тепмодинамики.
- •1.3. Уравнение состояния вещества
- •1.4. Методы расчета поля взрыва в газах и жидкостях
- •3.5. Простые волны
- •3.6. Волны сжатия
- •3.7. Волны разрежения. Разлет продуктов детонации в пустоту
- •4. Основы теории ударных волн
- •4.1. Законы сохранения на фронте прямых и косых ударных волн
- •4.3. Ударная адиабата
- •4.4. Двойное ударное сжатие
- •4.5. Температура при ударном и изоэнтропическом процессах в совершенном газе
- •4.6. Энтропия при ударном сжатии
- •4.7. Ударные волны разрежения и сжатия
- •4.8. Толщина фронта ударной волны
- •4.9. Сильные и слабые ударные волны в совершенном газе
- •4.10. Диссипация на фронте ударной волны
3.5. Простые волны
Как мы выяснили ранее, простые римановские волны описываются особыми решениями основной системы дифференциальных уравнений в виде (3.34), (3.35) для совершенного газа:
![]() (3.43)
(3.43)
где знаки выбираются следующим образом. Если волна распространяется вправо, в положительном направлении оси ox, то выбираются верхние знаки; если влево, в отрицательном направлении оси ox, то выбираются нижние знаки.
Рассмотрим характеристики простых волн.
Как было установлено, выражение (с плюсом или минусом):
![]() (3.44)
(3.44)
является характеристикой решений основной системы в плоскости u, c и представляет собой прямую линию. Так как мы рассматриваем одно уравнение (при решении конкретной задачи), то характеристика для данного особого решения - одна прямая линия, вдоль которой переносится постоянное значение выражения, например, ( рис.3.5)
Характеристики простой волны (3.43) в общем случае в плоскости x, t имеют вид (для системы с верхними знаками)
|
Рис. 3.5. Характеристика особого решения |
Возьмем на характеристике в плоскости u, c какую-нибудь точку 3. Эта точка будет определять состояние среды с фиксированными u1 и c3. Для данного фиксированного состояния имеем уравнение характеристики в плоскости x, t:
![]() (3.46)
(3.46)
Продифференцируем это выражение и получим скорость распространения данного фиксированного состояния среды
![]()
Итак, для каждого данного фиксированного состояния среды i в плоскости x, t имеем определенную прямую линию. Для другого фиксированного состояния будем иметь в плоскости x, t другую прямую линию (рис. 3.6).
|
Таким образом, каждой точке характеристики в плоскости u, c соответствует определенная характеристика в плоскости x, t. Далее рассмотрим несколько задач газовой динамики, которые описываются теорией простых римановских волн. |
3.6. Волны сжатия
Пусть мы имеем жесткую трубу с поршнем. В начальный момент времени поршень покоится и справа от него в трубе находится покоящийся совершенный газ с параметрами Pн, н, cн (рис.3.7а). Затем поршень начинает вдвигаться в трубу. От поршня вправо по |
|
газу пробежит волна сжатия. Движение газа в данном случае является плоским изоэнтропическим и граничит с областью покоя. Такое движение газа представляет собой простую волну и описывается особым решением.
Из двух особых решений данной задачи выбираем одно решение, при этом пользуемся правилом: если волны идут в положительном направлении оси ox, то выбираем особое решение из (3.43) с верхними знаками
![]() (3.47)
(3.47)
Величину константы определяем из граничных условий на фронте волны uн= 0, c = cн (см. рис. 3.7б)
![]() (3.48)
(3.48)
так как uH=0 (газ покоится), константа в нашем случае будет равна
![]() (3.49)
(3.49)
Рассмотрим качественную картину движения газа перед поршнем (при любом законе движения поршня). Подставим значение константы во второе уравнение системы (3.47)
![]() (3.50)
(3.50)
С другой стороны, мы имеем в простой волне (3.45)
![]()
Исключим с из этого выражения. Для этого выразим с из уравнения (3.50)
![]()
и подставим в уравнение
![]() (3.51)
(3.51)
Скорость поршня uн известна (предполагаем, что известен закон движения поршня), поэтому можем написать
![]() (3.52)
(3.52)
Таким образом, любое состояние газа,
которое возникает у поршня, передвигается
по газу со скоростью
![]() Определим наклон характеристик в
плоскости x, t
для некоторых фиксированных положений
поршня:
Определим наклон характеристик в
плоскости x, t
для некоторых фиксированных положений
поршня:
 (3.53)
(3.53)
Наклон характеристик
С физической точки зрения это объясняется тем, что каждая |
Рис. 3.8 . Семейство характеристик. |
последующая элементарная волна сжатия движется по газу, более уплотненному предыдущей волной, и амплитуда волны непрерывно увеличивается. Характеристики в конце концов пересекаются в какой-то точке (см. рис. 3.8). Поскольку вдоль каждой характеристики в плоскости x, t для простой волны параметры среды u и c постоянны, то в точке пересечения характеристик ( точка а на рис. 3.8) нарушается однозначность параметров среды. В точке пересечения характеристик возникает ударная волна (все параметры газа изменяются скачком) и течение становится неизоэнтропическим (в этом случае необходимо использовать адиабатические уравнения движения среды).
Уравнения (3.47) описывают движение газа в трубе только до момента образования ударной волны.
Проведенный выше анализ, следовательно, показывает, что в случае ускоренного движения поршня из волны сжатия формируется ударная волна.
Определим теперь функцию F(u). Для этого мы должны задать закон движения поршня.
Задача 1. Пусть в нашем случае поршень движется равноускоренно. Закон движения поршня описывается уравнениями (а - ускорение)
![]() (3.54)
(3.54)
Выразим функцию F(u) из первого уравнения (3.47)
![]()
Подставим в это уравнение выражения
для xп
и t из (3.54) с
учетом, что
![]() ,
и получим выражение для функции F(u):
,
и получим выражение для функции F(u):
![]() (3.55)
(3.55)
Теперь мы можем записать решение (3.47) нашей задачи в окончательном виде:
![]() (3.56)
(3.56)
|
На рис. 3.9 показана зависимость u=u(x) для разных моментов времени t.
Определим давление и плотность в волне
сжатия. Так как газ совершенный, то
есть
|
самой волне, записывается для скоростей звука и плотностей в виде
![]() (3.57)
(3.57)
или для давлений, плотностей и скоростей звука
![]() (3.58)
(3.58)
Поскольку закон изменения c = c(x, t) известен из уравнений (3.56), то соотношения (3.58) позволяют определить Р = Р(x, t) и = (x, t).
Теперь определим момент и координату образования ударной волны. В момент образования ударной волны производная скорости по координате x стремится к бесконечности, (см. рис. 3.9), то есть
![]() или
или
![]() (3.59)
(3.59)
Найдем эту производную и приравняем ее
к нулю. Уравнение (3.56) с учетом, что
![]() ,
можно записать в виде
,
можно записать в виде
![]() (3.60)
(3.60)
Продифференцируем это выражение по u и приравняем его к нулю:
![]() (3.61)
(3.61)
Выразим из этого уравнения время, которое и будет моментом образования ударной волны
![]() (3.62)
(3.62)
Минимальное время образования ударной волны соответствует u = 0. В этот момент времени пересекутся две первые характеристики (см. т. а на рис. 3.8) при u = 0 и образуется ударная волна
![]() (3.63)
(3.63)
Координата образования ударной волны
![]() (3.64)
(3.64)
Следует отметить, что с момента образования ударной волны перестают быть справедливыми уравнения, описывающие изоэнтропические, описывающие движение движения, так как после возникновения ударной волны энтропия каждой частицы среды изменится.
Поэтому уравнения волны сжатия, справедливы для времени t tУВ , тогда x xУВ.
В случае, если поршень мгновенно приобретает скорость, то есть a , то ударная волна возникает в момент времени tУВ= 0 и xУВ= 0.

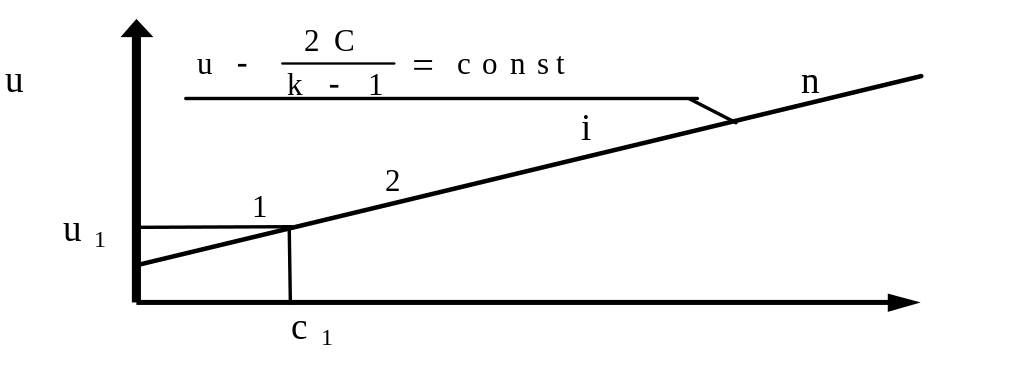
 Рис. 3.6. Семейство характеристик
Рис. 3.6. Семейство характеристик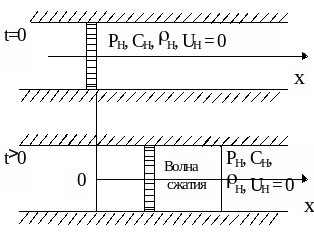 Рис.
3.7 . Расчетная схема (а, б)
Рис.
3.7 . Расчетная схема (а, б)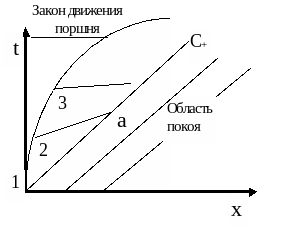
 Рис. 3.9 . Распределение
скоростей.
Рис. 3.9 . Распределение
скоростей.