1.4. Методы расчета поля взрыва в газах и жидкостях
В газовой динамике движение газа рассматривается как движение сплошной Среды, заполняющей все исследуемое пространство без образования пустот. Обычно параметры газа в разных точках пространства существенно отличаются друг от друга и такой газ является неравновесным. В классической термодинамике параметры неравновесного термодинамического тела (газа) вообще не подлежат рассмотрению. Поэтому в газодинамике важным является понятия элемента сплошной среды, объем которого настолько мал, что его можно считать точкой и настолько велик, чтобы содержащихся в нем частицу хватило для введения среднестатистических параметров газа. Данные элементы среды принято считать равновесными и для описания изменения их состояния за счет деформации и теплообмена можно применять уравнения равновесной термодинамики.
Таким образом движение газа можно рассматривать как механическое перемещение элементов среды изменяющих свое термодинамическое состояние.
Движение элементов среды описывается с помощью двух уравнений механики, отражающих законы сохранения массы и импульса, которые в газодинамике называются уравнениями неразрывности и количества движения.
Изменение состояния выделенных элементов описывается с помощью уравнения состояния и первого закона термодинамики, выражающего собой закон сохранения энергии. Обычно это уравнение преобразуется в уравнение изменения кинетической и внутренней энергии и в газовой динамике называется уравнением энергии.
Таким образом три дифференциальных уравнения, отражающих законы сохранения массы, импульса и энергии и алгебраическое уравнение состояния, составляют полную систему уравнений, позволяющих при известных начальных и граничных условиях определить параметры состояния газа (давление, температуру и плотность) и вектор скорости газа в каждой точке исследуемого пространства в каждый момент времени.
При изучении движения сплошной среды используются два метода: метод Лагранжа и метод Эйлера.
В методе Лагранжа отдельные частицы рассматривают как материальные точки, сплошь заполняющие некий вещественный объем. Изучение движения заключается в определении скорости, ускорения частиц и параметров состояния газа как функции времени и в исследовании изменения их при переходе от частицы к частице.
При таком подходе координаты (x, y, z) любой частицы жидкого объема в момент времени t можно рассматривать как функции времени и начального положения той же частицы (x0, y0, z0):
Вместо декартовых координат
можно взять любые три величины
связанные
с
однозначными
зависимостями, тогда x,
y, z можно
представить в виде функций от переменных
Лагранжа
.
Составляющие скорости и ускорения
определяются как первые и вторые
производные от координат:
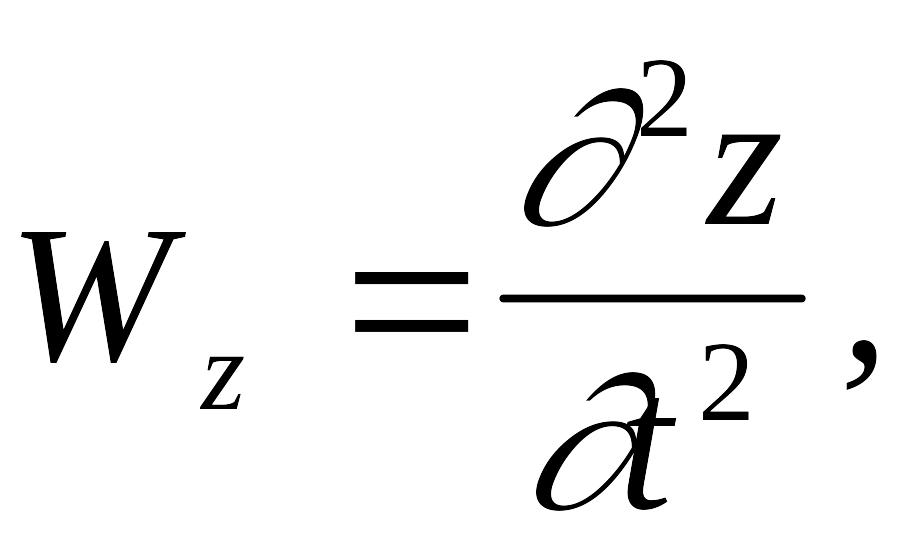
где
–– проекции скорости
и ускорения
на оси x, y,
z.
В методе Эйлера следует за изменением параметров газа в каждой отдельной точке исследуемого пространства то есть наблюдают за изменением во времени параметров движения частицы ( , ), проходящей через фиксированную точку пространства и за изменением их при переходе из одной тоски пространства в другую.
Таким образом при таком подходе скорость, ускорение, плоскость и другие параметры частиц будут функциями времени и координат:
,
,
Для каждой частицы жидкости
,
где
;
;
.
При определении ускорения в переменных
Эйлера надо учитывать как изменение
скорости в данной тоске во времени, так
и то, что через данную тоску проходят
разные частицы. То есть, если частица в
момент времени
имела координаты
и скорость
,
то за время
она переместиться в положение
,
,
и скорость ее станет
Тогда ускорение, характеризующее изменение скорости вдоль траектории движения частицы определится:
