18.14. Вариант 14

 18.14.1. Почему при физической интерпретации волновой функции говорят не о самой -функции, а о квадрате её модуля ?

 18.14.2. В потенциальной яме с бесконечно высокими стенками шириной электрон находится в возбужденном состоянии (n = 4). Сколько разных фотонов может быть излучено при его переходе в невозбужденное состояние?

 18.14.3. Электрон с энергией Е = 100 эВ попадает на потенциальный барьер высотой U = 64 эВ. Определите вероятность того, что электрон отразится от барьера.

 18.14.4. Определите энергию и длину волны излучения атома водорода при переходе 3 s – 2 p. Нарисуйте диаграмму энергетических уровней, проградуируйте шкалу в электрон вольтах и покажите этот переход.

 18.14.5. Двухатомная молекула с моментом инерции I = 1,16∙10^–39 г∙см² находится во вращательном состоянии с энергией Е_r = 1,8∙10^–3 эВ. Найдите частоту ω фотона (принадлежащего чисто вращательному спектру), который может испускать данная молекула при изменении своего вращательного состояния.

18.15. Вариант 15

 18.15.1. Докажите, что если ψ-функция циклически зависит от времени 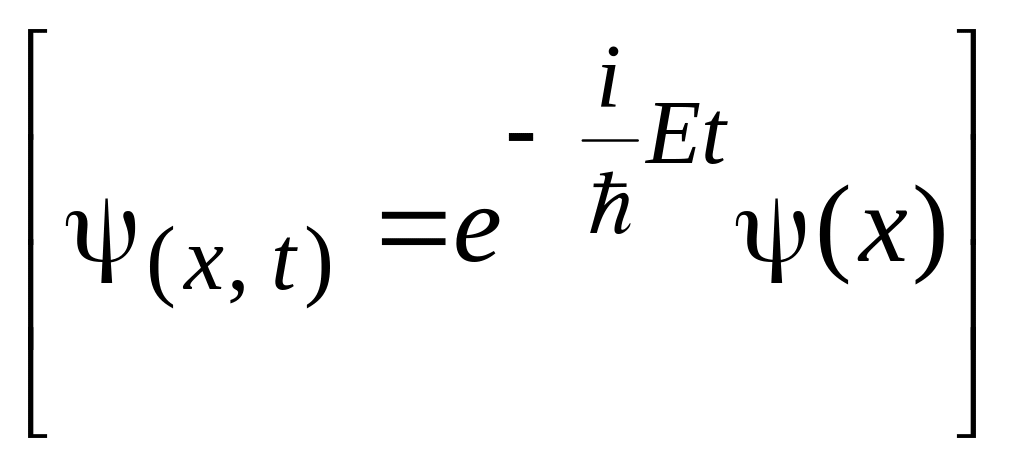, то плотность вероятности есть функция только координаты.

 18.15.2. Частица находится в потенциальном ящике. Найдите отношение разности соседних энергетических уровней ΔE_n+1,n к энергии E_n частицы в трех случаях: а) n = 3; б) n = 10; в) n = ∞. Поясните полученные результаты.

 18.15.3. Напишите уравнение Шредингера для электрона с энергией Е, движущегося в положительном направлении оси х для I и II областей, если на границе этих областей имеется низкий потенциальный барьер высотой U. Напишите решения уравнения Шредингера для I и II областей. Какой смысл имеют коэффициенты А₁ и B₁ для и А₂ и B₂ для ? Чему равен коэффициент В₂?

 18.15.4. Используя векторную модель атома, определите наименьший угол α, который может образовать вектор L момента импульса орбитального движения электрона в атоме с направлением внешнего магнитного поля. Электрон в атоме находится в d-состоянии.

 18.15.5. Собственная частота колебаний молекулы водорода ω = 8,25∙10¹⁴ с^–1, расстояние между ядрами d = 74 пм. Найдите отношение числа этих молекул на первом возбужденном колебательном уровне ( = 1) к числу молекул на первом возбужденном вращательном уровне (j = 1) при температуре Т = 785 К (кратность вырождения вращательных уровней = 2j+1).

18.16. Вариант 16

 18.16.1. Может ли быть больше единицы?

 18.16.2. Частица в бесконечно глубоком одномерном прямоугольном потенциальном ящике шириной находится в основном состоянии. Какова вероятность обнаружения частицы в крайней четверти ящика?

 18.16.3. Электрон обладает энергией  = 10 эВ. Определите, во сколько раз изменится его скорость V, длина волны де Бройля λ при прохождении через потенциальный барьер высотой U = 6 эВ.

 18.16.4. Атом водорода, находившийся первоначально в основном состоянии, поглотил квант света с энергией ε = 10,2 эВ. Определите изменение момента импульса ΔL орбитального движения электрона. В возбужденном атоме электрон находится в p-состоянии.

 18.16.5. Вычислите для молекулы HF число вращательных уровней, расположенных между нулевым и первым возбужденным колебательными уровнями. Собственная частота колебаний этой молекулы равна , а расстояние между ядрами d = 91,7 пм.