 18.7.2. Изобразите на графике вид первых трех собственных функций , описывающих состояние электрона в потенциальном ящике шириной , а также вид . Установите соответствие между числом N узлов волновой функции (т. е. числом точек, где волновая функция обращается в нуль в интервале 0 < x < ) и квантовым числом n.

 18.7.3. Электрон с энергией Е движется в одномерном потенциальном поле. Определите вероятность отражения R от данной прямоугольной ямы, если Е = 9 эВ, U₀ = 16 эВ, = 10^–8 см.

 18.7.4. Вычислите спиновой момент импульса для электрона в атоме водорода и величину проекции этого момента на направление внешнего магнитного поля.

 18.7.5. Определите, сколько линий содержит чисто вращательный спектр молекул СО. Момент инерции молекулы СО I = 1,44∙10^–39 г∙см².

18.8. Вариант 8

 18.8.1. Сформулируйте принцип соответствия и поясните суть этого принципа: а) на примере линейного гармонического осциллятора; б) на примере задачи об электроне в бесконечно глубоком потенциальном ящике.

 18.8.2. Частица в потенциальном ящике находится в основном состоянии. Какова вероятность обнаружить частицу: а) в средней трети ящика; б) в крайней трети ящика?

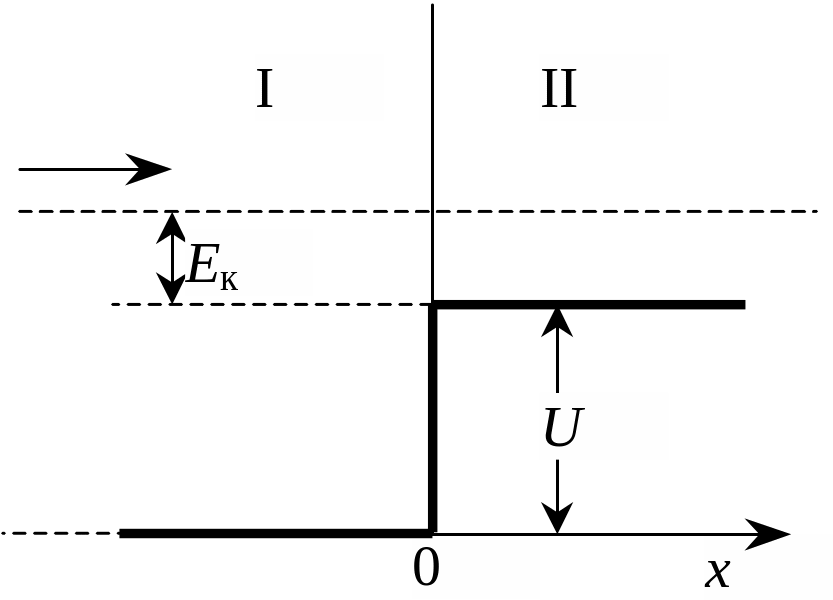
 18.8.3. Кинетическая энергия электрона Е_к в два раза превышает высоту U потенциального барьера. Определите коэффициент отражения R и коэффициент прозрачности D электронов на границе барьера.

 18.8.4. Заполненная электронная оболочка характеризуется квантовым числом n = 3. Укажите число электронов на этой оболочке, которые имеют одинаковыми следующие квантовые числа:

1) ; 2) ; 3) ; 4) и ;

5) и .

 18.8.5. Собственная круговая частота колебаний молекулы HF равна 7,79∙10¹⁴ с^–1. Между нулевым и первым возбужденным колебательными уровнями располагается 13 вращательных уровней. Определите расстояние d между центрами ядер в этой молекуле.

18.9. Вариант 9

 18.9.1. Временная часть уравнения Шредингера имеет вид . Найдите решение уравнения.

 18.9.2. Вычислите уровни энергии частицы массой 1 г в прямоугольной яме шириной 1 см. При каком n кинетическая энергия этой частицы равняется 1 Дж? Чему равен (в джоулях) интервал между значениями Е_n и E_n+1? Проявится ли дискретность энергетических состояний?

 18.9.3. Напишите выражение для в области II высокого потенциального барьера, если ψ функция нормирована так, что А₁ = 1. Определите плотность вероятности нахождения электрона в точке x = 0, если энергия Е, высота потенциального барьера U.

 18.9.4. Рассчитайте и постройте в масштабе схему первых четырех энергетических уровней атома водорода. Определите количество возможных переходов и длины волн соответствующих спектральных линий. Каким сериям они принадлежат?

 18.9.5. Вычислите величину В и первые четыре вращательных уровня энергии для молекулы N₂ (в её наинизшем электронном и колебательном состоянии). Вычислите длины волн линий чисто вращательного спектра N₂, отвечающего переходам между этими уровнями.

Молекула	, 1014 с–1	d, пм
N2	4,4	109,4

Здесь – собственная частота колебаний молекулы, d – расстояние между её ядрами.

18.10. Вариант 10

 18.10.1. Запишите условие нормирования волновой функции в случае движения частицы в пространстве и объясните физический смысл этого выражения.

 18.10.2. Запишите уравнение Шредингера и его решение для электрона в одномерной прямоугольной яме с бесконечно высокими стенками. Вычислите три уровня энергии в электрон-вольтах. Ширина ямы = 3 Å. Какую долю составляет энергия электрона в основном состоянии от энергии покоя m₀c²? Существенны ли релятивистские эффекты при вычислениях с шириной ямы такого порядка, типичного для внешних электронов в атомах и молекулах?

 18.10.3. Электрон с энергией Е = 5 эВ налетает на потенциальный барьер треугольной формы. Высота барьера U₀ = 6 эВ, а ширина у основания = 1 Å. Найдите коэффициент прохождения D электрона через данный барьер.

 18.10.4. В атоме К, L и М – оболочки заполнены полностью. Определите: а) общее число электронов в атоме; б) число s-, p- и d- электронов; в) сколько p-электронов имеют квантовое число m = 0?

 18.10.5. Вычислите расстояние d между ядрами молекулы HCl исходя из того, что некоторые из линий её вращательного спектра имеют длины волн λ = 120,3 мк; 96,0 мк; 80,4 мк; 68,9 мк; 60,4 мк.