
- •1.Магнитное поле и его св-ва
- •4. Движение заряженной частицы в однородном магнитном поле. Применение силы Лоренца
- •5.Явление электромагнитной индукции
- •1) При выведении его из положения равновесия в системе возникает сила, направленная к положению равновесия;
- •2) Трение в колебательной системе достаточно мало.
- •17. Зная, как связаны между собой ускорение и координата колеблющегося тела, можно на основе математического анализа найти зависимость координаты от времени.
- •23. Аналогия между механическими и электромагнитными колебаниями
- •28. Перейдем к более детальному рассмотрению процессов, которые происходят в цепи, подключенной к источнику переменного напряжения.
- •1. Для чего нужна модуляция колебаний! 2. Что называют детектированием колебаний!
28. Перейдем к более детальному рассмотрению процессов, которые происходят в цепи, подключенной к источнику переменного напряжения.
Сила
тока в цени с резистором. Пусть
цепь состоит из соединительных проводов
и нагрузки с малой индуктивностью и
большим сопротивлением R (рис. 4.10). Эту
величину, которую мы до сих пор называли
электрическим сопротивлением или просто
сопротивлением, теперь будем называть
активным сопротивлением.
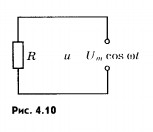 Сопротивление R
называется активным, потому что при
наличии нагрузки, обладающей этим
сопротивлением, цепь поглощает энергию,
поступающую от генератора. Эта
энергия превращается во внутреннюю
энергию проводников — они нагреваются.
Будем считать, что напряжение на
зажимах цепи меняется по гармоническому
закону:
u = Um cos
t.
Как
и в случае постоянного тока, мгновенное
значение силы тока прямо пропорционально
мгновенному значению напряжения. Поэтому
для нахождения мгновенного значения
силы тока можно применить закон
Ома:
Сопротивление R
называется активным, потому что при
наличии нагрузки, обладающей этим
сопротивлением, цепь поглощает энергию,
поступающую от генератора. Эта
энергия превращается во внутреннюю
энергию проводников — они нагреваются.
Будем считать, что напряжение на
зажимах цепи меняется по гармоническому
закону:
u = Um cos
t.
Как
и в случае постоянного тока, мгновенное
значение силы тока прямо пропорционально
мгновенному значению напряжения. Поэтому
для нахождения мгновенного значения
силы тока можно применить закон
Ома:
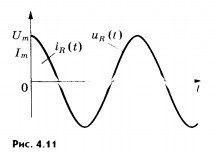
![]() В
проводнике с активным сопротивлением
колебания силы тока совпадают по фазе
с колебаниями напряже ния (рис. 4.11), а
амплитуда силы тока определяется
равенством
В
проводнике с активным сопротивлением
колебания силы тока совпадают по фазе
с колебаниями напряже ния (рис. 4.11), а
амплитуда силы тока определяется
равенством
![]() Мощность
в цепи с резистором. В
цепи переменного тока промышленной
частоты (v = 50 Гц) сила тока и напряжение
изменяются сравнительно быстро. Поэтому
при прохождении тока по проводнику,
например по нити электрической лампочки,
количество выделенной энергии также
будет быстро меняться со временем. Но
этих быстрых изменений мы не замечаем.
Мощность
в цепи с резистором. В
цепи переменного тока промышленной
частоты (v = 50 Гц) сила тока и напряжение
изменяются сравнительно быстро. Поэтому
при прохождении тока по проводнику,
например по нити электрической лампочки,
количество выделенной энергии также
будет быстро меняться со временем. Но
этих быстрых изменений мы не замечаем.
Как правило, нам нужно бывает знать среднюю мощ ностъ тока на участке цепи за большой промежуток времени, включающий много периодов. Для этого достаточно найчи среднюю мощность за один период. Под средней за период, мощностью переменного тока понимают отношение суммарной энергии, поступающей в цепь за период, к периоду.
Мощность
в цепи постоянного тока на участке с
сопротивлением R определяется формулой
P
= I2R.
(4.18)
На протяжении очень малого
интервала времени переменный ток можно
считать практически постоянным.
 Поэтому
мгновенная моoность в цепи переменного
тока на участке, имеющем активное
сопротивление R, определяется формулой
P
= i2R.
(4.19)
Найдем среднее
значение мощности за период. Для этого
сначала преобразуем формулу (4.19),
подставляя в нее выражение (4.16) для силы
тока и используя известное из математики
соотношение
Поэтому
мгновенная моoность в цепи переменного
тока на участке, имеющем активное
сопротивление R, определяется формулой
P
= i2R.
(4.19)
Найдем среднее
значение мощности за период. Для этого
сначала преобразуем формулу (4.19),
подставляя в нее выражение (4.16) для силы
тока и используя известное из математики
соотношение
![]()
![]() График
зависимости мгновенной мощности от
времени изображен на рисунке 4.12, а.
Согласно графику (рис. 4.12, б.), на протяжении
одной восьмой периода, когда
График
зависимости мгновенной мощности от
времени изображен на рисунке 4.12, а.
Согласно графику (рис. 4.12, б.), на протяжении
одной восьмой периода, когда
![]() ,
мощность в любой момент времени больше,
чем
,
мощность в любой момент времени больше,
чем
![]() .
Зато на протяжении следующей восьмой
части периода, когда cos 2
t
< 0, мощность в любой момент времени
меньше чем
.
Среднее за период значение cos 2
t
равно нулю, а значит равно нулю второе
слагаемое в уравнении (4.20).
Средняя
мощность
.
Зато на протяжении следующей восьмой
части периода, когда cos 2
t
< 0, мощность в любой момент времени
меньше чем
.
Среднее за период значение cos 2
t
равно нулю, а значит равно нулю второе
слагаемое в уравнении (4.20).
Средняя
мощность
![]() равна,
таким образом, первому члену в формуле
(4.20):
равна,
таким образом, первому члену в формуле
(4.20):
![]() Действующие
значения силы тока и напряжения. Из
формулы (4.21) видно, что величина
Действующие
значения силы тока и напряжения. Из
формулы (4.21) видно, что величина
![]() есть среднее за период значение квадрата
силы тока:
есть среднее за период значение квадрата
силы тока:
 Величина,
равная квадратному корню из среднего
значения квадрата силы тока, называется
действующим значением силы неременного
тока. Действующее зртачепие силы
неременного тока обозначается через
I:
Величина,
равная квадратному корню из среднего
значения квадрата силы тока, называется
действующим значением силы неременного
тока. Действующее зртачепие силы
неременного тока обозначается через
I:
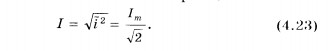 Действующее
значение силы переменного тока равно
силе такого постоянного тока, при котором
в проводнике выделяется то же
количество теплоты,
что и при переменном токе за то же время.
Действующее
значение силы переменного тока равно
силе такого постоянного тока, при котором
в проводнике выделяется то же
количество теплоты,
что и при переменном токе за то же время.
Действующее
значение переменного напряжения
определяется аналогично действующему
значению силы тока:
![]() Заменяя
в формуле (4.17) амплитудные значения силы
тока и напряжения на их действующие
значения, получаем
Заменяя
в формуле (4.17) амплитудные значения силы
тока и напряжения на их действующие
значения, получаем
![]() Это
закон Ома для участка цепи переменного
тока с резистором.
Это
закон Ома для участка цепи переменного
тока с резистором.
Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры ивольтметры переменного тока.
Кроме того, действующие значения удобнее мгновенных значений еще и потому, что именно они непосредственно определяют среднее значение мощности Р переменного тока: P = I2R = UI. Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется действующими значениями силы тока и напряжения.
29. Постоянный ток не может идти по цепи, содержащей конденсатор. Ведь фактически при этом цепь оказывается разомкнутой, так как обкладки конденсатора разделены диэлектриком.
Переменный же ток может идти по цепи, содержащей конденсатор. В этом можно убедиться с помощью простого опыта.
Пусть у нас имеются источники постоянного и переменного напряжений, причем постоянное напряжение на зажимах источника равно действующему значению переменного напряжения. Цепь состоит из конденсатора и лампы накаливания (рис. 4.13), соединенных последовательно. При включении постоянного напряжения (переключатель повернут влево, цепь подключена к точкам АА') лампа не светится. Но при включении переменного напряжения (переключатель повернут вправо, цепь подключена к точкам ВВ') лампа загорается, если емкость конденсатора достаточно велика.
Как же переменный ток может идти по цепи, если она фактически разомкнута (между пластинами конденсатора заряды перемещаться не могут)? Все дело в том, что происходит периодическая зарядка и разрядка конденсатора под действием переменного напряжения. Ток, идущий в цепи при перезарядкеконденсатора, нагревает нить лампы.
Установим, как меняется со временем сила тока в цепи, содержащей только конденсатор, если сопротивлением проводов и обкладок конденсатора можно пренебречь (рис. 4.14).
Напряжение
на конденсаторе
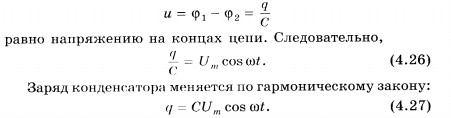 Сила
тока, представляющая собой производную
заряда по времени, равна:
Сила
тока, представляющая собой производную
заряда по времени, равна:
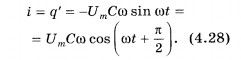
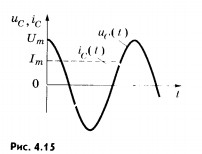
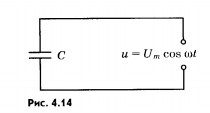 Следовательно,
колебания силы тока опережают по фазе
колебания напряжения
на конденсаторе на
(рис.
4.15).
Следовательно,
колебания силы тока опережают по фазе
колебания напряжения
на конденсаторе на
(рис.
4.15).
 Амплитуда
силы тока равна:
Im =
UmC
.
(4.29)
Если ввести обозначение
Амплитуда
силы тока равна:
Im =
UmC
.
(4.29)
Если ввести обозначение
![]() и
вместо амплитуд силы тока и напряжения
использовать их действующие значения,
то получим
и
вместо амплитуд силы тока и напряжения
использовать их действующие значения,
то получим
 Величину
Xc,
обратную произведению
С
циклической частоты на электрическую
емкость конденсатора, называют емкостным
сопротивлением. Роль этой величины
аналогична роли активного сопротивления
R в законе Ома (см. формулу (4.17)). Действующее
значение силы тока связано с действующим
значением напряжения на конденсаторе
точно так же, как связаны согласно закону
Ома сила тока и напряжение для участка
цепи постоянного тока. Это и позволяет
рассматривать величину Хс как
сопротивление конденсатора переменному
току (емкостное сопротивление).
Величину
Xc,
обратную произведению
С
циклической частоты на электрическую
емкость конденсатора, называют емкостным
сопротивлением. Роль этой величины
аналогична роли активного сопротивления
R в законе Ома (см. формулу (4.17)). Действующее
значение силы тока связано с действующим
значением напряжения на конденсаторе
точно так же, как связаны согласно закону
Ома сила тока и напряжение для участка
цепи постоянного тока. Это и позволяет
рассматривать величину Хс как
сопротивление конденсатора переменному
току (емкостное сопротивление).
Чем больше емкость конденсатора, тем больше ток перезарядки. Это легко обнаружить по увеличению накала лампы при увеличении емкости конденсатора. В то время как сопротивление конденсатора постоянному току бесконечно велико, его сопротивление переменному току имеет конечное значение Xc. С увеличением емкости оно уменьшается. Уменьшается оно и с увеличением частоты .
В заключение отметим, что на протяжении четверти периода, когда конденсатор заряжается до максимального напряжения, энергия поступает в цепь и запасается в конденсаторе в форме энергииэлектрического поля. В следующую четверть периода, при разрядке конденсатора, эта энергия возвращается в сеть.
Сопротивление цепи с конденсатором обратно пропорционально произведению циклической частоты на электроемкость. Колебания силы тока опережают по фазе колебания напряжения на .
30.
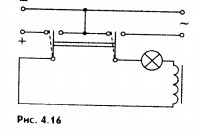
Индуктивность в цепи влияет на силу переменного тока. Это можно доказать с помощью простого опыта.
Соберем цепь из катупхки с большой индуктивностью и электрической лампы накаливания (рис. 4.16). С помощью переключателя можно подк.тючить эту цепь либо к источнику постоянного напряжения, либо к источнику переменного напряжения. При этом постоянное напряжение и действующее значение переменного напряжения должны быть равны. Опыт показывает, что лампа светится ярче при постоянном напряжении. Следовательно, действующее значение силы переменного тока в рассматриваемой цепи меньше силы постоянного тока.
Объясняется это различие явлением самоиндукции. В § 15 главы 2 рассказывалось о том, что при подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно. Возникающее при этом вихревое электрическое поле тормозит движение электронов. Лишь по прошествии некоторого времени сила тока достигает наибольшего (установившегося) значения, соответствующего данному постоянному напряжению.
Если напряжение быстро меняется, то сила тока не будет успевать достигнуть тех значений, которые она приобрела бы с течением времени при постоянном напряжении.
Следовательно, максимальное значение силы переменного тока (его амплитуда) ограничивается индуктивностью цепи и будет тем меньше, чем больше индуктивность и чем больше частота приложенного напряжения.
Определим
силу тока в цепи, содержащей катушку,
активным сопротивлением которой можно
пренебречь (рис. 4.17). Для этого предварительно
найдем связь между напряжением на
катушке и ЭДС самоиндукции в ней.
 Если
сопротивление катушки равно нулю, то и
напряженность электрического поля
внутри проводника в любой момент времени
должна быть равна нулю. Иначе сила тока,
согласно закону
Ома,
была бы бесконечно большой. Равенство
нулю напряженности поля оказывается
возможным потому, что напряженность
вихревого электрического поля
i,
порождаемого переменным магнитным
полем, в каждой точке равна по модулю и
противоположна по направлению
напряженности кулоновского поля
k,
создаваемого в проводнике зарядами,
расположенными на зажимах источника и
в проводах цепи.
Если
сопротивление катушки равно нулю, то и
напряженность электрического поля
внутри проводника в любой момент времени
должна быть равна нулю. Иначе сила тока,
согласно закону
Ома,
была бы бесконечно большой. Равенство
нулю напряженности поля оказывается
возможным потому, что напряженность
вихревого электрического поля
i,
порождаемого переменным магнитным
полем, в каждой точке равна по модулю и
противоположна по направлению
напряженности кулоновского поля
k,
создаваемого в проводнике зарядами,
расположенными на зажимах источника и
в проводах цепи.
Из
равенства
i =
-
k следует,
что удельная работа вихревого поля (т.
е. ЭДС самоиндукции еі)
равна по модулю и противоположна по
знаку удельной работе кулоновского
поля. Учитывая, что удельная работа
кулоновского поля равна напряжению на
концах катушки, можно записать:
еі =
-и.
При изменении силы тока по
гармоническому закону
i = Im
sin
t
ЭДС
самоиндукции равна:
eі =
- Li'
= - L
lm cos
t.
(4.32)
Так как u = -еі,
то напряжение на концах катушки
оказывается равным
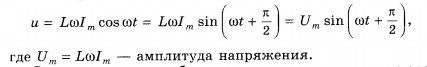 Следовательно,
колебания напряжения на катушке опережают
по фазе колебания силы тока на
,
или, что то же самое, колебания си.яы
тока отстают по фазе от колебаний напряжения
на
(рис.
4.18).
Следовательно,
колебания напряжения на катушке опережают
по фазе колебания силы тока на
,
или, что то же самое, колебания си.яы
тока отстают по фазе от колебаний напряжения
на
(рис.
4.18).
Амплитуда силы тока в катушке равна:
 и
вместо амплитуд силы тока и напряжения
использовать их действующие значения,
то получим:
и
вместо амплитуд силы тока и напряжения
использовать их действующие значения,
то получим:
![]() Величину
XL,
равную произведению циклической частоты
на индуктивность,
называют индуктивным сопротивлением.
Величину
XL,
равную произведению циклической частоты
на индуктивность,
называют индуктивным сопротивлением.
Согласно формуле (4.35) действующее значение силы тока связано с действующим значением напряжения и индуктивным сопротивлением соотношением, подобным закону Ома для цепи постоянного тока.
Индуктивное сопротивление зависит от частоты . Постоянный ток вообще «не замечает» индуктивности катушки. При = 0 индуктивное сопротивление равно нулю (XL = 0).
Чем быстрее меняется напряжение, тем больше ЭДС самоиндукции и тем меньше амплитуда силы тока.
Катушка индуктивности оказывает сопротивление переменному току. Это сопротивление, называемое индуктивным, равно произведению циклической частоты на индуктивность. Колебания силы тока в цепи с индуктивностью отстают по фазе от колебаний напряжения на .
31. Действующие значения силы тока и напряжения. Из формулы (4.21) видно, что величина есть среднее за период значение квадрата силы тока: Величина, равная квадратному корню из среднего значения квадрата силы тока, называется действующим значением силы неременного тока. Действующее зртачепие силы неременного тока обозначается через I: Действующее значение силы переменного тока равно силе такого постоянного тока, при котором в проводнике выделяется то же количество теплоты, что и при переменном токе за то же время.
Действующее значение переменного напряжения определяется аналогично действующему значению силы тока: Заменяя в формуле (4.17) амплитудные значения силы тока и напряжения на их действующие значения, получаем Это закон Ома для участка цепи переменного тока с резистором.
Как и при механических колебаниях, в случае электрических колебаний обычно нас не интересуют значения силы тока, напряжения и других величин в каждый момент времени. Важны общие характеристики колебаний, такие, как амплитуда, период, частота, действующие значения силы тока и напряжения, средняя мощность. Именно действующие значения силы тока и напряжения регистрируют амперметры ивольтметры переменного тока.
Кроме того, действующие значения удобнее мгновенных значений еще и потому, что именно они непосредственно определяют среднее значение мощности Р переменного тока: P = I2R = UI. Колебания силы тока в цепи с резистором совпадают по фазе с колебаниями напряжения, а мощность определяется действующими значениями силы тока и напряжения.
32.
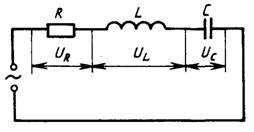
Закон Ома для переменного тока — Если ток является синусоидальным с циклической частотой ω, а цепь содержит не только активные, но и реактивные компоненты (ёмкости, индуктивности), то закон Ома обобщается
![]()
Полное
сопротивление : ![]()
Сила переменного тока определяется при заданном напряжении не только сопротивлением R, которым обладает данная цепь при постоянном токе, но и наличием в этой цепи конденсаторов или катушек индуктивности. Поэтому, величины R и Z различны, т. е. одна и та же цепь будет иметь различное сопротивление для постоянного и для переменного тока.
В Формуле мы использовали :
![]() —
Напряжение
(разность потенциалов)
—
Напряжение
(разность потенциалов)
![]() —
Сила тока
—
Сила тока
![]() —
Полное
сопротивление
—
Полное
сопротивление
![]() —
Реактивное
сопротивление
—
Реактивное
сопротивление
 —
Активное
сопротивление
—
Активное
сопротивление
При изучении вынужденных механических колебаний мы ознакомились с явлением резонанса. Резонанс наблюдается в том случае, когда собственная частота колебаний системы совпадает с частотой изменения внешней силы. Если трение мало, то амплитуда установившихся вынужденных колебаний при резонансе резко увеличивается. Совпадение вида уравнений для описания механических и электромагнитных колебаний (позволяет сделать заключение о возможности резонанса также и в электрической цепи, если эта цепь представляет собой колебательный контур, обладающий определенной собственной частотой колебаний.
При
механических колебаниях резонанс
выражен отчетливо при малых значениях
коэфициента трения
![]() .
В электрической цепи роль коэффициента
трения выполняет ее активное сопротивление
R. Ведь именно наличие этого сопротивления
в цепи приводит к превращению энергии
тока но внутреннюю энергию проводника
(проводник нагревается). Поэтому резонанс
в электрическом колебательном кон-lype
должен быть выражен отчетливо при малом
активном сопротивлении R.
.
В электрической цепи роль коэффициента
трения выполняет ее активное сопротивление
R. Ведь именно наличие этого сопротивления
в цепи приводит к превращению энергии
тока но внутреннюю энергию проводника
(проводник нагревается). Поэтому резонанс
в электрическом колебательном кон-lype
должен быть выражен отчетливо при малом
активном сопротивлении R.
Мы
с вами уже знаем, что если активное
сопротивление мало, то собственная
циклическая частота колебаний в контуре
определяется формулой
![]() Сила
тока при вынужденных
колебаниях должна
достигать максимальных значений, когда
частота переменного напряжения,
приложенного к контуру, равна собственной
частоте колебательного контура:
Сила
тока при вынужденных
колебаниях должна
достигать максимальных значений, когда
частота переменного напряжения,
приложенного к контуру, равна собственной
частоте колебательного контура:
![]() Резонансом
в электрическом колебательном
контуре называется
явление резкого возрастания амплитуды
вынужденных колебаний силы тока при
совпадении частоты внегннего переменного
напряжения с собственной частотой
колебательного контура.
Резонансом
в электрическом колебательном
контуре называется
явление резкого возрастания амплитуды
вынужденных колебаний силы тока при
совпадении частоты внегннего переменного
напряжения с собственной частотой
колебательного контура.
Амплитуда силы тока при резонансе. Как и в случае механического резонанса, при резонансе в колебательном контуре создаются оптимальные условия для поступления энергии от внешнего источника в контур. Мощность в контуре максимальна в том случае, когда сила тока совпадает по фазе с напряжением. Здесь наблюдается полная аналогия с механическими колебаниями: при резонансе в механической колебательной системе внешняя сила (аналог напряжения в цепи) совпадает по фазе со скоростью (аналог силы тока).
Не
сразу после включения внешнего переменного
напряжения в цепи устанавливается
резонансное значение силы тока. Амплитуда
колебаний силы тока нарастает постепенно
— до тех пор, пока энергия, выделяющаяся
за период на резисторе, не сравняется
с энергией,
поступающей в контур за это же
время:
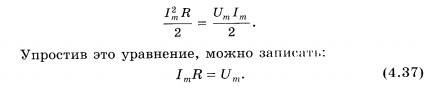 Отсюда
амплитуда установившихся колебаний
силы тока при резонансе определяется
уравнением
Отсюда
амплитуда установившихся колебаний
силы тока при резонансе определяется
уравнением
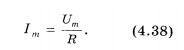 При
R
При
R
![]() 0
резонансное значение силы тока
неограниченно возрастает: (Im)рез
0
резонансное значение силы тока
неограниченно возрастает: (Im)рез
![]() .
Наоборот, с увеличением R максимальное
значение силы тока уменьшается, и при
больших R говорить о резонансе уже не
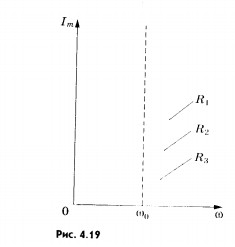
имеет смысла. Зависимость амплитуды
силы тока от частоты при различных
сопротивлениях (R1 <
R2 <
R3)
показана на рисунке 4.19.
.
Наоборот, с увеличением R максимальное
значение силы тока уменьшается, и при
больших R говорить о резонансе уже не
имеет смысла. Зависимость амплитуды
силы тока от частоты при различных
сопротивлениях (R1 <
R2 <
R3)
показана на рисунке 4.19.
 Одновременно
с увеличением силы тока при резонансе
резко возрастают напряжения на
конденсаторе и катушке индуктивности.
Эти напряжения при ма.пом активном
сопротивлении во много раз превышают
внешнее напряжение.
Одновременно
с увеличением силы тока при резонансе
резко возрастают напряжения на
конденсаторе и катушке индуктивности.
Эти напряжения при ма.пом активном
сопротивлении во много раз превышают
внешнее напряжение.
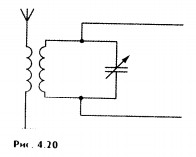
Использование
резонанса в радиосвязи. Явление
электрического резонанса широко
используется при осуществлении
радиосвязи. Радиоволны от различных
передающих станций возбуждают в
антеннерадиоприемника переменные
токи различных частот, так как каждая
передающая радиостанция работает на
своей частоте. С антенной индуктивно
связан колебательный контур (рис. 4.20).
Вследствие электромагнитной индукции
в контурной катушке возникают переменные
ЭДС соответствующих частот и вынужденные
колебания силы тока тех же частот. Но
только при резонансе колебания силы
тока в контуре и напряжения в нем будут
значительными, т. е. из колебаний различных
частот, возбуждаемых в антенне, контур
выделяет только те, частота которых
равна его собственной частоте. Настройка
контура на нужную частоту
обычно
осуществляется путем изменения
емкости конденсатора.
В этом обычно состоит настройка радиоприемника на
определенную радиостанцию.
 Необходимость
учета возможности резонанса в электрической
цепи. В некоторых случаях резонанс в
электрической цепи может принести
большой вред. Если цепь не рассчитана
на работу в условиях резонанса, то его
возникновеие может привести к аварии.
Необходимость
учета возможности резонанса в электрической
цепи. В некоторых случаях резонанс в
электрической цепи может принести
большой вред. Если цепь не рассчитана
на работу в условиях резонанса, то его
возникновеие может привести к аварии.
Чрезмерно большие токи могут перегреть провода. Большие напряжения приводят к пробою изоляции.
Такого рода аварии нередко случались еще сравнительно недавно, когда плохо представляли себе законы электрических колебаний и не умели правильно рассчитывать электрические цепи.
При вынужденных электромагнитных колебаниях возможен резонанс — резкое возрастание амплитуды колебаний силы тока и напряжения при совпадении частоты внешнего переменного напряжения с собственной частотой колебаний. На явлении резонанса основана вся радиосвязь.
33.
Отдельные частицы любого тела -твердого, жидкого или газообразного — взаимодействуют друг с другом. Поэтому если какая-либо частица тела начинает совершать колебательные движения, то в результате взаимодействия между частицами это движение начинает с некоторой скоростью распространяться во все стороны.
Волна — это колебания, распространяющиеся в пространстве с течением времени.
В воздухе, твердых телах и внутри жидкостей механические волны возникают благодаря действию сил упругости. Эти силы осуществляют связь между отдельными частями тела. Образование волн на поверхности воды вызывают сила тяжести и сила поверхностного натяжения.
Наиболее отчетливо главные особенности волнового движения можно увидеть, если рассматривать волны на поверхности воды. Это могут быть, например, волны, которые представляют собой бегущие вперед округлые валы. Расстояния между валами, или гребнями, примерно одинаковы. Однако если на поверхности воды, по которой бежит волна, находится легкий предмет, например лист с дерева, то он не будет увлекаться вперед волной, а начнет соверпгать колебания вверх и вниз, оставаясь почти на одном месте.
При возбуждении волны происходит процесс распространения колебаний, но не перенос вещества. Возникшие в каком-то месте колебания воды, например от брошенного камня, передаются соседним участкам и постепенно распространяются во все стороны, вовлекая в колебательные движения все новые и новые частицы среды. Течение же воды не возникает, перемещаются лишь локальные формы ее поверхности.
Рассмотрим
физические характеристики волны —
длину волны и скорость.
После того как колебания при распространении
поперечной волны достигнут 13-го шара,
1-й и 13-й шары будут колебаться совершенно
одинаково. Когда 1-й шар находится в
положении равновесия и движется влево
(если смотреть вдоль цепочки шаров; см.
рис. 6.7, д), то и 13-й шар находится в
положении равновесия и тоже движется
влево. Спустя еще четверть периода 1 й
шар оказывается максимально отклоненным
влево и в гаком же положении находится
13-й шар (см. рис. 6.7, е). Колебания этих
шаров происходят в одинаковых
фазах1.
1Точнее,
колебания 13-го шара отстают по фазе от
колебаний 1-го на 2
.
Но так как cos (
t
- 2
)
= cos
t,
то такая разность фаз не приводит к
различию в состояниях колеблющихся
шаров, и можно считать поэтому, что
их колебания происходят в одинаковых
фазах.
Кратчайшее
расстояние между точками, колеблющимися
в одинаковых фазах, называется длиной
волны. Следо-иательно, расстояния между
1-ми 13-м, 2-м и 14-м, 3-м и 15-м шарами равны
длине волны (см. рис. 6.7, д, с). Длина полны
обозначается греческой буквой
![]() (лямбда).
(лямбда).
Длина продольной волны согласно рисунку 6.8, б равна расстоянию между 4-м и 16-м шарами или между 2-м и 14-м шарами.
При распространении волны разные частицы среды (шары в рассматриваемой модели) колеблются с различными фазами, если только расстояние между ними не равно n (где n — целое число).
Шары 1-й и 7-й (см. рис. 6.7), находящиеся на расстоянии /2, колеблются в противоположных фазах: когда 1-й шар от положения равновесия движется вверх, то 7-й — вниз (см. рис. 6.7, d).
За
один период волна распространяется на
расстояние
(см.
рис. 6.7, д).
=
T.
(6.1)
Длина
волны —
это расстояние, на которое распространяется
волна за время, равное одному
периодуколебаний.
Так как период Т и частота v связаны
соотношением
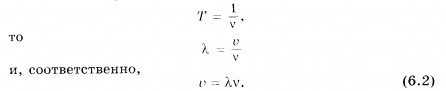 При
распространении волны вдоль шнура мы
наблюдаем два вида периодичности.
При
распространении волны вдоль шнура мы
наблюдаем два вида периодичности.
Во-первых, каждая частица шнура совершает периодические колебания во времени. В случаегармонических колебаний (эти колебания происходят по закону синуса или косинуса) частота и амплитуда колебаний частиц одинаковы во всех точках шнура. Эти колебания различаются только фазами.
Во-вторых, в каждый момент времени форма волны (т. е. профиль шнура) повторяется на протяжении шнура через отрезки длиной . На рисунке 6.9 черной линией показан профиль шнура в определенный момент времени t (мгновенный снимок волны). С течением времени этот профиль перемещается.
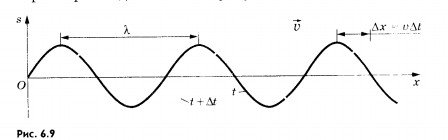 Спуста
промежуток времени
t
волна будет иметь вид, изображенный на
том же рисунке синей линией.
Спуста
промежуток времени
t
волна будет иметь вид, изображенный на
том же рисунке синей линией.
Для продольной волны также справедлива формула (6.2), связывающая скорость распространения волны, длину волны и частоту колебаний.
34.
Упругие
волны, распространяясь в воздухе,
а также внутри жидкостей и твердых тел,
невидимы. Однако при определенных
условиях их можно услышать.
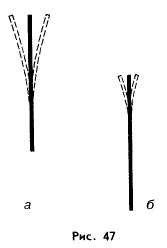
Обратимся
к опыту. Зажмем в тисках длинную
стальную линейку. Если над тисками будет
выступать большая часть линейки (рис.
47, а), то, вызвав ее колебания, мы не
услышим порождаемые ею волны. Но если
укоротить выступающую часть линейки и
тем самым увеличить частоту ее колебаний,
то мы обнаружим, что линейка начнет
звучать (рис. 47, б).
 Упругие
волны, способные вызывать у человека
слуховые ощущения, называются звуковыми
волнами или
просто звуком.
Упругие
волны, способные вызывать у человека
слуховые ощущения, называются звуковыми
волнами или
просто звуком.
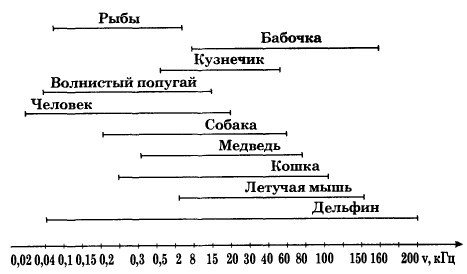
Человеческое ухо способно воспринимать упругие волны с частотой примерно от 16 Гц до 20 кГц. Поэтому частоты в диапазоне от 16 Гц до 20 кГц называют звуковыми. Любое тело, колеблющееся со звуковой частотой, является источником звука, так как в окружающей его среде возникают распространяющиеся от него звуковые волны.
Животные
в качестве звука воспринимают волны
иных частот.
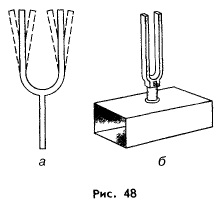
 Существуют
как естественные, так и искусственные
источники звука. Один из искусственных
источников звука - камертон -
изображен на рисунке 48. Он был изобретен
в 1711 г. английским музыкантом Дж. Шором
для настройки музыкальных инструментов.
Существуют
как естественные, так и искусственные
источники звука. Один из искусственных
источников звука - камертон -
изображен на рисунке 48. Он был изобретен
в 1711 г. английским музыкантом Дж. Шором
для настройки музыкальных инструментов.
Камертон
представляет собой изогнутый (в виде
двух ветвей) металлический стержень с
держателем посередине. Ударив резиновым
молоточком по одной из ветвей камертона,
мы услышим определенный звук. Этот звук
возникает после удара по камертону: его
ветви начинают вибрировать, создавая
вокруг себя попеременные сжатия и
разрежения воздуха (рис. 48, а). Распространяясь
по воздуху, эти возмущения образуют
звуковую волну.
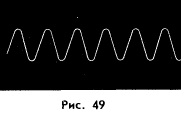
 Стандартная
частота колебаний камертона 440 Гц. Это
означает, что за 1 с его ветви успевают
совершить 440 колебаний. На глаз они
незаметны. Если, однако, прикоснуться
к звучащему камертону рукой, то можно
почувствовать его вибрацию. Для
определения характера колебаний
камертона к одной из его ветвей следует
прикрепить иглу. Заставив камертон
звучать, проведем соединенной с ним
иглой по поверхности закопченной
стеклянной пластинки. На пластинке
появится след в форме синусоиды (рис.
49).
Стандартная
частота колебаний камертона 440 Гц. Это
означает, что за 1 с его ветви успевают
совершить 440 колебаний. На глаз они
незаметны. Если, однако, прикоснуться
к звучащему камертону рукой, то можно
почувствовать его вибрацию. Для
определения характера колебаний
камертона к одной из его ветвей следует
прикрепить иглу. Заставив камертон
звучать, проведем соединенной с ним
иглой по поверхности закопченной
стеклянной пластинки. На пластинке
появится след в форме синусоиды (рис.
49).
 Для
усиления звука, создаваемого камертоном,
его держатель укрепляют на деревянном
ящике, открытом с одной стороны (см. рис.
48, б). Этот ящик называют резонатором.
При колебаниях камертона вибрация ящика
передается находящемуся в нем воздуху.
Из-за резонанса, возникающего при
правильно подобранных размерах ящика,
амплитуда вынужденных колебаний воздуха
возрастает, и звук усиливается. Его
усилению способствует и увеличение
площади излучающей поверхности, которое
имеет место при соединении камертона
с ящиком.
Для
усиления звука, создаваемого камертоном,
его держатель укрепляют на деревянном
ящике, открытом с одной стороны (см. рис.
48, б). Этот ящик называют резонатором.
При колебаниях камертона вибрация ящика
передается находящемуся в нем воздуху.
Из-за резонанса, возникающего при
правильно подобранных размерах ящика,
амплитуда вынужденных колебаний воздуха
возрастает, и звук усиливается. Его
усилению способствует и увеличение
площади излучающей поверхности, которое
имеет место при соединении камертона
с ящиком.
Нечто подобное происходит и в таких музыкальных инструментах, как гитара, скрипка и т. д. Сами по себе струны этих инструментов создают слабый звук. Громким он становится благодаря наличию у них корпуса определенной формы с отверстием, через которое могут выходить звуковые волны.
Источниками звука могут быть не только колеблющиеся твердые тела, но и некоторые явления, вызывающие колебания давления в окружающей среде (взрывы, полет пуль, завывания ветра и т.д.). В качестве наиболее яркого примера такого явления можно назвать молнию. Во время грозы температура в канале молнии увеличивается до 30 000 °С. Давление резко возрастает, и в воздухе возникает ударная волна, постепенно переходящая в звуковые колебания (с типичной частотой 60 Гц), распространяющиеся в виде раскатов грома.
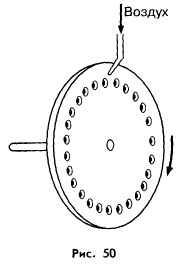
Интересным
источником звука является дисковая
сирена,
изобретенная немецким физиком Т. Зеебеком
(1770-1831). Она представляет собой соединенный
с электродвигателем диск с отверстиями,
расположенный перед сильной струей
воздуха (рис. 50). При вращении диска поток
воздуха, проходящего через отверстия,
периодически прерываемся, в результате
чего возникает резкий характерный звук.
Частота этого звука находится по формуле
v = nk, где n - частота вращения диска; k -
число отверстий в нем.
 Используя
сирену с несколькими рядами отверстий
и регулируемой частотой вращения диска,
можно получить звуки разной частоты.
Частотный диапазон сирен, применяемых
на практике, составляет обычно от 200 Гц
до 100 кГц и выше.
Используя
сирену с несколькими рядами отверстий
и регулируемой частотой вращения диска,
можно получить звуки разной частоты.
Частотный диапазон сирен, применяемых
на практике, составляет обычно от 200 Гц
до 100 кГц и выше.
Свое название эти источники звука получили по имени полуптиц-полуженщин, которые, согласно древнегреческим мифам, завлекали своим пронзительным пением мореходов на кораблях, и те разбивались о прибрежные скалы.
В газах и жидкостях звуковые волны распространяются в виде продольных волн сжатия и разрежения(рис. 51). Сжатия и разрежения среды, возникающие вследствие колебаний источника звука (колокольчика, струны, камертона, мембраны телефона, голосовых связок и т.д.), через некоторое время достигают человеческого уха и, заставляя барабанную перепонку уха совершать вынужденные колебания, вызывают у человека определенные слуховые ощущения. Человеческое ухо очень чувствительный прибор. Воспринимать звук мы начинаем уже тогда, когда амплитуда колебаний частиц воздуха в волне оказывается равной всего лишь радиусу атома!
С возрастом из-за потери эластичности барабанной перепонки верхняя граница воспринимаемых человеком частот постепенно снижается. Лишь молодые люди способны слышать звуки с частотой 20 кГц. В среднем и тем более в старшем возрасте как мужчины, так и женщины перестают воспринимать звуковые волны, частота которых превышает 12-14 кГц.
Ухудшается слух людей и в результате длительного воздействия громких звуков. Работа вблизи мощных самолетов, в очень шумных заводских цехах, частое посещение дискотек и чрезмерное увлечение аудиоплеерами вредно влияют на остроту восприятия звуков (особенно высокочастотных) и в некоторых случаях могут привести к потере слуха.
35.
Выведем уравнение волны, которое позволит определить смещение каждой точки среды в любой момент времени при распространении гармонической волны.
Сделаем это на примере волны, бегущей по длинному тонкому резиновому шнуру.
Ось ОХ направим вдоль шнура, а начало отсчета свяжем с левым концом шнура. Смещение колеблющейся точки шнура от положения равновесия обозначим буквой s. Для описания волнового процесса нужно знать смещение каждой точки шнура в любой момент времени. Следовательно, надо знать вид функции S = s(x, t). Заставим конец шнура (точка с координатой х = 0) совершать гармонические колебания с циклической частотой (0. Колебания этой точки будут происходить по закону: s = sm sin t, (6.3) если начальную фазу колебаний считать равной нулю. Здесь, sm — амплитуда колебаний (рис. 6.10, а).
Колебания
распространяются вдоль шнура (оси ОХ)
со cкоростью
и
в произвольную точку шнура с
координатой
![]() прийдут
спустя время
прийдут
спустя время

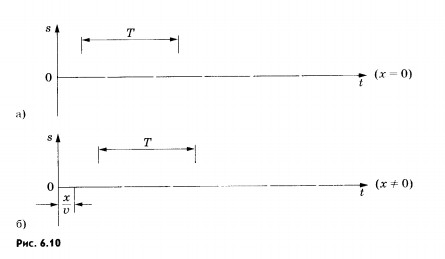 Эта
точка также начнет совершать гармонические
колебания с
частотой
,
но с запаздыванием на время
(рис.
6.10, б). Если пренебречь затуханием волны
по мере ее распространения, то колебания
в точке х будут происходить с той же
амплитудой sm,
но с другой фазой:
Эта
точка также начнет совершать гармонические
колебания с
частотой
,
но с запаздыванием на время
(рис.
6.10, б). Если пренебречь затуханием волны
по мере ее распространения, то колебания
в точке х будут происходить с той же
амплитудой sm,
но с другой фазой:
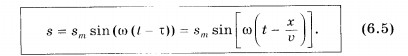 Это
и есть уравнение гармонической бегущей
волны,
распространяющейся в положительном
направлении оси Ох.
Это
и есть уравнение гармонической бегущей
волны,
распространяющейся в положительном
направлении оси Ох.
36.
Электрический ток никогда не получил бы такого широкого применения, если бы его нельзя было преобразовывать почти без потерь энергии.
Назначение трансформаторов. ЭДС мощных генераторов электростанций довольно велика. Между тем в практике чаще всего нужно не слишком высокое напряжение.
Преобразование переменного тока, при котором напряжение увеличивается или уменьшается в несколько раз практически без потери мощности, осуществляется с помощью трансформаторов.
Впервые
трансформаторы были использованы в
1878 г. русским ученым П.Н.Яблочковым для
питания изобретенных им электрических
свечей — нового в то время
источника света.
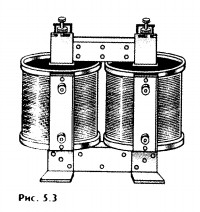 Устройство
трансформатора. Трансформатор
состоит из замкнутого стального
сердечника, собранного из пластин, на
который надеты две (иногда и более)
катушки с проволочными обмотками (рис.
5.3). Одна из обмоток, называемая первичной,
подключается к источнику переменного
напряжения. Другая обмотка, к которой
присоединяют нагрузку, т. е. приборы и
устройства, потребляющие электроэнергию,
называется вторич ной. Условное
обозначение трансформатора приведено
на рисунке 5.4.
Устройство
трансформатора. Трансформатор
состоит из замкнутого стального
сердечника, собранного из пластин, на
который надеты две (иногда и более)
катушки с проволочными обмотками (рис.
5.3). Одна из обмоток, называемая первичной,
подключается к источнику переменного
напряжения. Другая обмотка, к которой
присоединяют нагрузку, т. е. приборы и
устройства, потребляющие электроэнергию,
называется вторич ной. Условное
обозначение трансформатора приведено
на рисунке 5.4.
Работа нагруженного трансформатора. Если к концам вторичной обмотки присоединить цепь, потребляющую электроэнергию, или, как говорят, нагрузить трансформатор, то сила тока во вторичной обмотке уже не будет равна нулю. Появившийся ток создаст в сердечнике свой переменный магнитный поток, который будет уменьшать изменения магнитного потока в сердечнике.
Уменьшение
амплитуды колебаний результирующего
магнитного потока, казалось бы должно,
в свою очередь, уменьшить ЭДС индукции
в первичной обмотке. Это, однако, не
произойдет, так как согласно формуле
(5.3)
![]() .
Поэтому при замыкании цепи вторичной
обмотки автоматически увеличится сила
тока в первичной обмотке. Его амплитуда
возрастет таким образом, что восстановится
прежнее значение амплитуды колебаний
результирующего магнитного потока.
.
Поэтому при замыкании цепи вторичной
обмотки автоматически увеличится сила
тока в первичной обмотке. Его амплитуда
возрастет таким образом, что восстановится
прежнее значение амплитуды колебаний
результирующего магнитного потока.
Увеличение
силы тока в цепи первичной обмотки
происходит в соответствии с законом
сохранения энергии: отдача электроэнергии
в цепь, присоединенную к вторичной
обмотке трансформатора, сопровождается
потреблением от сети такой же энергии
первичной обмоткой. Мощность в первичной
цепи при нагрузке трансформатора,
близкой к номинальной, примерно равна
мощности во вторичной цепи:
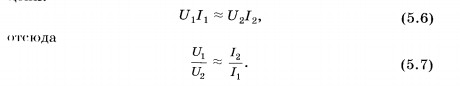 Это
означает, что, повышая с помощью
трансформатора нанрлжение в несколько
раз, мы во столько же раз уменьшаем силу
тока (и наоборот).
Это
означает, что, повышая с помощью
трансформатора нанрлжение в несколько
раз, мы во столько же раз уменьшаем силу
тока (и наоборот).
Трансформатор преобразует переменный электрический ток таким образом, что произведение силы тока на напряжение примерно одинаково в первичной и вторичной обмотках.
37.
Механические волны распространяются только в упругих средах: газе, жидкости или твердом теле. Существуют, однако, волны, которые не нуждаются в каком-либо веществе для своего распространения. Это электромагнитные волны. К ним, в частности, относятся радиоволны и свет. Электромагнитное поле может существовать в вакууме, т. е. в пространстве, не содержащем атомов. Несмотря па существенное отличие электромагнитных волн от механических, электромагнитные волны нри распространении ведут себя подобно механическим.
Электромагнитная волна. Представьте себе, что электрический заряд не просто сместился из одной точки в другую, а был приведен в быстрые колебания вдоль некоторой прямой. Заряд движется подобно телу, подвешенному на пружине, но только колебания его происходят со значительно большей частотой. Тогда электрическое поле в непосредственной близости от заряда начнет периодически изменяться. Период этих изменений, очевидно, будет равен периоду колебаний заряда. Переменное электрическое поле будет пороледать периодически меняющееся магнитное поле, а оно, в свою очередь, вызовет появление переменного электрического поля уже на большем расстоянии от заряда и т. д.
В окружающем заряд пространстве, захватывая все большие и большие области, возникает система взаимно перпендикулярных, периодически изменяющихся электрических и магнитных полей. На рисунке 7.1 изображен «мгновенный снимок» такой системы полей на большом расстоянии от колеблющегося заряда.
На этом рисунке показаны векторы и в различных точках пространства. Направление Z -— одно из направлений распространения электромагнитных возмущений.
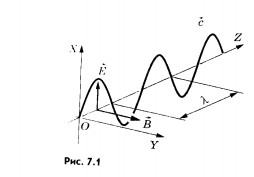
Образуется так называемая электромагнитная волна, бегущая по всем направлениям от колеблющегося заряда.
В каждой точке пространства электрические и магнитные поля меняются во времени периодически. Чем дальше расположена точка от заряда, тем позднее достигнут ее колебания векторов и . Следовательно, на разных расстояниях от заряда колебания каждого из этих векторов происходят с различными фазами.
Колебания векторов и в любой точке совпадают по фазе. Кратчайшее расстояние между двумя ближайшими точками, в которых колебания происходят в одинаковых фазах, есть длина волны данный момент времени векторы и меняются в пространстве по оси Z по закону синуса с периодом .
Направления этих двух колеблющихся векторов — напряженности электрического поля и индукции магнитного поля — перпендикулярны направлению распространения волны. Электромагнитная волна является поперечной.
Таким
образом, векторы
и
в
электромагнитной волне перпендикулярны
друг к другу и перпендикулярны направлению
распространения волны. Если вращать
буравчик с правой нарезкой от вектора
к
вектору
,
то поступательное перемещение буравчика
будет совпадать с направлением вектора
скорости волны
![]() .
(см. рис. 7.1).
.
(см. рис. 7.1).
Излучение электромагнитных волн. Электромаг
Обнаружение.
Как мы уже знаем, электромагнитная волна образуется в результате взаимной связи переменных электрических и магнитных полей. Изменение одного поля приводит к появлению другого.
В § 12 и 17 говорилось, что, чем быстрее меняется со временем магнитная индукция, тем болыпе напряженность возникающего электрического поля. И в свою очередь, чем быстрее меняется напряженность электрического поля, тем болыпе магнитная индукция.
Следовательно, для образования интенсивных элек тротагнитных волн необходимо создать электромагнитные колебания достаточно высокой частоты. Именно при этом условии напряженность электрического поля и индукция магнитного поля будут меняться быстро.
Колебания
высокой частоты, значительно превышающей
частоту промышленного тока (50 Гц), можно
получить с помощью колебательного
контура. Циклическая частота колебаний
будет тем больше, чем меньше индуктивность L
и емкость С контура.
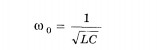 Открытый
колебательный контур. Однако
большая частота электромагнитных
колебаний еще не гарантирует интенсивного
излучения электромагнитных волн. В
обычном контуре, какой изображен на
рисунке 4.3 (его можно назвать закрытым),
почти все магнитное поле сосредоточено
внутри катушки, а электрическое — внутри
конденсатора. Вдали от контура
электромагнитного поля практически
нет. Такой контур очень слабо из.чучает
электромагнитные волны.
Открытый
колебательный контур. Однако
большая частота электромагнитных
колебаний еще не гарантирует интенсивного
излучения электромагнитных волн. В
обычном контуре, какой изображен на
рисунке 4.3 (его можно назвать закрытым),
почти все магнитное поле сосредоточено
внутри катушки, а электрическое — внутри
конденсатора. Вдали от контура
электромагнитного поля практически
нет. Такой контур очень слабо из.чучает
электромагнитные волны.
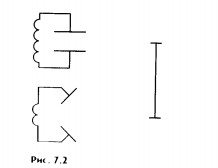
Для получения электромагнитных волн Г. Герц использовал простое устройство, которое в его честь было названо вибратором Герца. Это устройство представляет собой открытый колебательный контур.
К открытому контуру можно перейти от закрытого, если постепенно раздвигать пластины конденсатора(рис. 7.2), уменьшая их площадь и одновременно уменьшая число витков в катушке. В конце концов получится просто прямой провод. Это и есть открытый колебательный контур. Емкость и индуктивность вибратора Герца малы. Потому соответствующая им частота колебаний весьма велика.
В
открытом контуре заряды не сосредоточены
на его концах, а распределены по всему
проводнику. Ток в данный момент времени
во всех сечениях проводника направлен
в одну и ту же сторону, но сила тока
неодинакова в различных сечениях
проводника. На концах она равна нулю, а
посредине достигает максимума. (Напомним,
что в обычных цепях переменного тока
сила тока во всех сечениях в данный
момент времени одинакова.) Электромагнитное
поле охватывает все пространство вблизи
контура.
 Для
возбуждения колебаний в таком контуре
во времена Герца поступали
так. Провод разрезали
посредине с таким расчетом, чтобы
оставался небольшой воздушный промежуток,
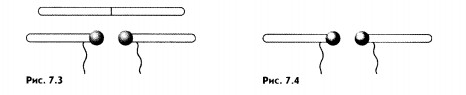
называемый искровым (рис. 7.3).
Для
возбуждения колебаний в таком контуре
во времена Герца поступали
так. Провод разрезали
посредине с таким расчетом, чтобы
оставался небольшой воздушный промежуток,
называемый искровым (рис. 7.3).
Обе части проводника заряжали до высокой разности потенциалов. Когда разность потенциалов превышала некоторое предельное значение, проскакивала искра (рис. 7.4), цепь замыкалась, и в открытом контуре возникали колебания.
Герц получал электромагнитные волны, возбуждая в вибраторе с помощью источника высокого напряжения серию импульсов быстропеременного тока. Колебания электрических зарядов в вибраторе создают электромагнитную волну. Только колебания в вибраторе совершает не одна заряженная частица, а огромное число электронов, движущихся согласованно. В электромагнитной волневекторы и перпендикулярны друг другу. В данном случае вектор лежит в плоскости, проходящей через вибратор, а вектор перпендикулярен этой плоскости. Излучение волн происходит с максимальной интенсивностью в направлении, перпендикулярном оси вибратора. Вдоль этой оси излучения не происходит.
Электромагнитные
волны регистрировались Герцем с помощью
приемного вибратора (резонатора),
представляющего собой такое же устройство,
как и излучающий вибратор.
 Под
действием переменного электрического
поля электромагнитной волны в приемном
вибраторе возбуждаются колебания тока.
Если собственная частота приемного
вибратора совпадает с частотой
электромагнитной волны, наблюдается
резонанс. Колебания в резонаторе
происходят с больпхей амплитудой при
расположении его параллельно излучающему
вибратору. Герц обнаружил эти колебания,
наблюдая искорки в очень маленьком
промежутке между проводниками приемного
вибратора.
Под
действием переменного электрического
поля электромагнитной волны в приемном
вибраторе возбуждаются колебания тока.
Если собственная частота приемного
вибратора совпадает с частотой
электромагнитной волны, наблюдается
резонанс. Колебания в резонаторе
происходят с больпхей амплитудой при
расположении его параллельно излучающему
вибратору. Герц обнаружил эти колебания,
наблюдая искорки в очень маленьком
промежутке между проводниками приемного
вибратора.
Ученый не только получил электромагнитные волны, но и открыл, что они ведут себя подобно другим видам волн. В частности, он наблюдал отражение электромагнитных волн от металлического листа и сложение волн. При сложении волны, идущей от вибратора, с волной, отраженной от металлического листа, образуются максимумы и минимумы амплитуды колебаний — так называемая интерференционная картина (подробнее об интерференции см. § 67—69). Если перемещать резонатор, можно найти положения максимумов и определить д.яину волны.
Скорость
электромагнитных волн.
В опытах Герца длина волны составляла
несколько десятков сантиметров. Вычислив
собственную частоту электромагнитных
ко.тебаний вибратора. Герц смог определить
скорость электромагнитной волны по
формуле
=
v.
Она оказалась приближенно равной
скорости света: с
![]() 300
000 км/с.
300
000 км/с.
Опытами Герца были блестяще подтверждены предсказания Максвелла.
Для излучения электромагнитных волн нужно создать электромагнитные колебания высокой частоты в открытом колебательном контуре.
38.
Принципы радиосвязи заключаются в следующем. Переменный электрический ток высокой частоты, созданный в передающей антенне, вызывает в окружающем пространстве быстроменяющееся элек тромагнитное поле, которое распространяется в видеэлектромагнитной волны. Достигая приемной антенны, электромагнитная волна вызывает в ней переменный ток той же частоты, на которой работает передатчик.
Важнейшим этапом в развитии радиосвязи было создание в 191.3 г. генератора незатухающих электромагнитных колебаний. Кроме передачи телеграфных сигналов, состоящих из коротких и более продолжительных импульсов («точки» и «тире») электромагнитных волн, стала возможной надежная и высококачественная радиотелефонная связь — передача речи и музыки с помощью электромагнитных волн.
Радиотелефонная связь. При радиотелефонной связи колебания давления воздуха в звуковой волне превращаются с помощью микрофона в электрические колебания той же формы. Казалось бы, если эти колебания усилить и подать в антенну, то можно будет передавать на расстояние речь и музыку с помощью электромагнитных волн.
Однако в действительности такой способ передачи неосуществим. Дело в том, что частота звуковых колебаний мала, а электромагнитные волны низкой (звуковой) частоты имеют малую интенсивность.
Модуляция. Для осуществления радиотелефонной связи необходимо использовать высокочастотные колебания, интенсивно излучаемые антенной. Незатухающие гармонические колебания высокой частоты вырабатывает генератор, например генератор на транзисторе.
Для передачи звука эти высокочастотные колебания изменяют, или, как говорят, модулируют, с помощью электрических колебаний низкой (звуковой) частоты. Можно, например, изменять со звуковой частотой амплитуду высокочастотных колебаний. Этот способ называют амплитудной модуляцией.
На рисунке 7.8 приведены три графика: а) график колебаний высокой частоты, которую называют несущей частотой; б) график колебаний звуковой частоты, т. е. модулирующих колебаний; в) график модулированных по амплитуде колебаний.
Без модуляции мы в лучшем случае хможем контролировать лишь, работает станция или молчит. Без модуляции нет ни те.пеграфной, ни телефонной, ни телевизионной передачи.
Модуляция — медленный процесс. Это такие изменения в высокочастотной колебательной системе, при которых она успевает совершить очень много высокочастотных колебаний, прежде чем их амплитуда изменится заметным образом.
Детектирование. В приемнике из модулированных колебаний высокой частоты выделяются низкочастотные колебания. Такой процесс преобразования сигнала называют детектированием.
Полученный в результате детектирования сигнал соответствует тому звуковому сигналу, который действовал на микрофон передатчика. После усиления колебания низкой частоты могут быть превращены взвук.
Основные принципы радиосвязи представлены в виде блок-схемы на рисунке 7.9.
