ВВЕДЕНИЕ
С задачей распознавания образов живые системы, в том числе и человек, сталкиваются постоянно с момента своего появления. В частности, информация, поступающая с органов чувств, обрабатывается мозгом, который в свою очередь сортирует информацию, обеспечивает принятие решения, а далее с помощью электрохимических импульсов передает необходимый сигнал далее, например, органам движения, которые реализуют необходимые действия. Затем происходит изменение окружающей обстановки, и вышеуказанные явления происходят заново. И если разобраться, то каждый этап сопровождается распознаванием.
С развитием вычислительной техники стало возможным решить ряд задач, возникающих в процессе жизнедеятельности, облегчить, ускорить, повысить качество результата. К примеру, работа различных систем жизнеобеспечения, взаимодействие человека с компьютером, появление роботизированных систем и др. Тем не менее, отметим, что обеспечить удовлетворительный результат в некоторых задачах (распознавание быстродвижущихся подобных объектов, рукописного текста) в настоящее время не удается.
Первые исследования с вычислительной техникой в основном следовали классической схеме математического моделирования – математическая модель, алгоритм и расчет. Таковыми были задачи моделирования процессов происходящих при взрывах атомных бомб, расчета баллистических траекторий, экономических и прочих приложений. Однако помимо классических идей этого ряда возникали и методы, основанные на совершенно иной природе, и как показывала практика решения некоторых задач, они зачастую давали лучший результат, нежели решения, основанные на переусложненных математических моделях.
Уже сейчас распознавание образов плотно вошло в повседневную жизнь и является одним из самых насущных знаний современного инженера. В медицине распознавание образов помогает врачам ставить более точные диагнозы, на заводах оно используется для прогноза брака в партиях товаров. Именно поэтому к развитию распознавания образов с самого начала было приковано немало внимания со стороны специалистов самого различного профиля – кибернетиков, нейрофизиологов, психологов, математиков, экономистов и т.д.
1 Постановка задачи
Целью написания курсового проекта является создание программного обеспечения, позволяющего пользователю обрабатывать изображения, получать статистические данные и описывать контуры объектов на изображении.
Полученный программный продукт должен:
обеспечивать загрузку изображения;
обеспечивать возможность зашумления и фильтрации текущего изображения;
обеспечивать выделение границ на изображении с помощью методов обнаружения границ заданных по варианту;
обеспечивать описание контура объекта по индивидуальному варианту;
иметь удобный пользовательский интерфейс.
Программный продукт должен быть разработан на языке высокого уровня в виде MDI-приложения.
Разработанный программный продукт может быть использован в медицине, биологии и т.д.
2 Описание реализуемых методов и алгоритмов
2.1 Методы обработки изображений
В задачах обработки изображений последние нередко интерпретируются как случайные процессы двух переменных, т.е. как случайные поля. Это оправдано хотя бы потому, что при формировании изображений практически всегда имеются шумы. Следствием указанной интерпретации является то, что для обработки изображений могут, и в ряде случаев успешно, применяться статистические методы обработки информации, которые позволяют теоретически рассчитывать эффективность некоторых процедур обработки бинарных изображений.
Гистограмма изображения.
Когда на практике имеем дело с реальными изображениями, то заранее не известно ни закона распределения яркости, ни его параметров, но есть возможность получить оценку плотности распределения яркости не зависящую от вида закона и параметров. Оценкой плотности является гистограмма, представляющая собой графическое изображение, рассчитанное по реальным данным плотности распределения случайной величины.
Среди множества числовых характеристик изображений, рассматриваемых как реализации случайного поля, выделим несколько наиболее употребительных:
математическое ожидание;
среднеквадратическое отклонение;
коэффициенты асимметрии и эксцесса;
энтропия;
значения максимального и минимального элементов анализируемого поля;
размах (диапазон уровней);
моды.
Начальные моменты
Математическая
статистика оперирует с оценками указанных
моментов. Применительно к анализу
изображения
размером
элементов соответствующая формула
приобретает вид:
.
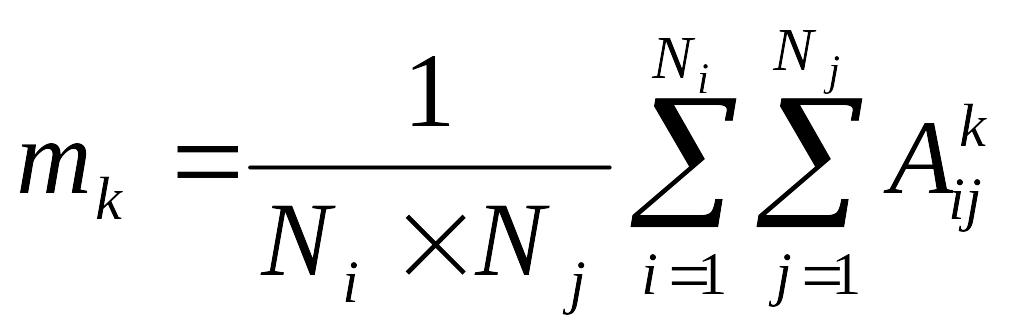(2.1)
В терминах математической статистики множество пикселей представляющих изображение является выборкой. Количество использованных для анализа пикселей будем называть объемом выборки.
Отметим еще раз, что статистический анализ (вычисление моментов, формирование гистограмм и т.п.) может быть выполнен не только для всего изображения, но и для любого заданного фрагмента. Существуют и более изощренные приемы. Так, в ряде случаев, используется так называемый «анализ по маске», когда обрабатываются элементы поля, образующие заданную маской конфигурацию. Анализ по маске позволяет определять статистические свойства отдельных объектов изображения, выделенных известными методами, а также произвольно заданных областей.
Учитывая сказанное, выражение (1.2) переписывается без указания явно границы суммирования следующим образом:
,
(2.2)
где
–
количество обработанных пикселей
исходного изображения (в данном случае
–
).
Центральные моменты
Для получения центральных моментов сначала необходимо вычислить начальные моменты по одной из выше приведенных формул, а затем использовать известные выражения для пересчета начальных моментов в центральные:
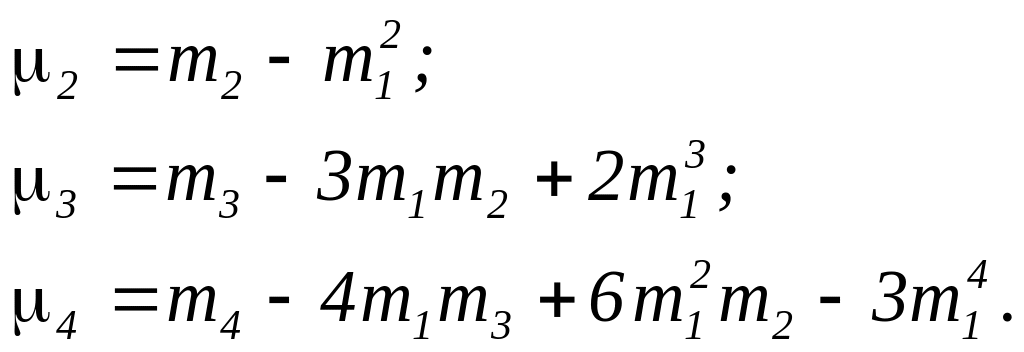(2.3)
Математическое ожидание
Как
мы уже говорили, начальный момент первого
порядка
называется математическим ожиданием,
или средним.
При этом значения яркости всех точек в сумме равноправны. Иногда используется взвешенное среднее, когда значение яркости каждой точки входит в сумму со своим «весом» – коэффициентом I(x,y), определяющим важность этой точки. В этом случае, величина суммы яркостей делится не на количество точек, а на сумму их весов:
.
(2.4)
Дисперсия
Центральный
момент второго порядка
называется дисперсией.
Аналогично можно определить взвешенную дисперсию:
. (2.5)
Часто на практике используют квадратный корень из дисперсии, называемый средним квадратическим отклонением:
, (2.6)
имеющий размерность яркости. Эта величина сокращенно называется СКО.
Дисперсия и среднеквадратическое отклонение характеризуют рассеяние яркости вокруг среднего значения.
Коэффициент асимметрии
С
центральным моментом третьего порядка
связан коэффициент асимметрии As,
характеризующий «скошенность»
распределения вероятностей:
.
(2.7)
Для симметричного (относительно математического ожидания) распределения коэффициент асимметрии равен нулю. Если он положителен, распределение яркости более пологое в области больших значений, если отрицателен – меньших.
Коэффициент эксцесса
С
центральным моментом четвертого порядка
связан коэффициент эксцесса Ex,
характеризующий «крутость» распределения:
.
(2.8)
Коэффициент эксцесса характеризует отличие формы распределения от нормального закона, т.е. нулевое значение коэффициента эксцесса соответствует нормальному распределению. Чтобы обеспечить такое его свойство, в формуле (1.8) и вычитается тройка. Если кривая плотности вероятностей имеет более острую и высокую вершину по сравнению с нормальным распределением, то эксцесс положителен; если более низкую и пологую – отрицателен.
Мода
Еще один простой, но важный параметр случайной величины носит название моды. Мода - это точка, в которой случайная величина имеет максимальную вероятность (имеется в виду локальный максимум). Как известно локальных максимумов может быть несколько. Соответственно, распределения, имеющие один, два или более максимумов, называются одномодальными, двухмодальными или многомодальными.
2.2 Алгоритмы подавления шума
Шумоподавляющая фильтрация изображения
Реальные изображения редко бывают идеального качества, практически всегда на них присутствует шум, под шумом будем понимать искажение яркости некоторых групп пикселей или совершенно неправильные значения отдельных групп пикселей никак не связанных с реальными значениями.
По способу искажения изображения шум можно разделить на несколько разновидностей:
аддитивный шум - к значению цвета или яркости каждого пиксела добавляется некоторая случайная величина, значения которой в каждой точке различны;
мультипликативный шум - значение цвета или яркости каждого пиксела умножается на некоторую случайную величину, значения которой близки к единице и в каждой точке различны;
импульсный шум - значения цвета или яркости некоторых отдельных пикселов искажаются настолько, что теряют всякую информацию об их неискаженных значениях.
Осреднение скользящим окном
Самый простой фильтр из линейных.
(2.9)
(2.10)
Недостатки: приводит к появлению на изображении структур в виде квадрата. Искажает или удаляет тонкие линии и мелкие детали и размывает границы контрастных областей.
Фильтр медианный
Один из видов цифровых фильтров, широко используемый в цифровой обработке сигналов и изображений для уменьшения уровня шума.
Значения отсчётов внутри окна фильтра сортируются в порядке возрастания (убывания); и значение, находящееся в середине упорядоченного списка, поступает на выход фильтра. В случае четного числа отсчетов в окне выходное значение фильтра равно среднему значению двух отсчетов в середине упорядоченного списка. Окно перемещается вдоль фильтруемого сигнала и вычисления повторяются.
9 10 10 10 11 11 12
12 13 (2.11)
Недостаток: плохо сохраняет структуру углов и тонких линий.
Фильтр Гаусса
Фильтр Гаусса обычно используется в цифровом виде для обработки двумерных сигналов (изображений) с целью снижения уровня шума. Однако при ресемплинге (изменение частоты дискретизации сигнала) он дает сильное размытие изображения.
(2.12)
Сигма-фильтр
Осредняются
значения только тех соседних пикселей,
чьи значения находятся в пределах
от значения центрального пикселя в
окне.
с – некоторый коэффициент
– СКО
всего изображения
(2.13)
(2.14)
(2.15)
2.3 Методы обнаружения границ объектов на изображении
Выделение границ – термин в теории обработки изображения и компьютерного зрения, частично из области поиска объектов и выделения объектов, основывается на алгоритмах которые выделяют точки цифрового изображения в которых резко изменяется яркость или есть другие виды неоднородностей.
Основной целью обнаружения резких изменений яркости изображения является фиксация важных событий и изменений мира. Они могут отражать различные предположения о модели формирования изображения, изменения в яркости изображения могут указывать на:
изменения глубины;
изменения ориентации поверхностей;
изменения в свойствах материала;
различие в освещении сцены.
Оператор Робертса
Оператор Робертса – один из ранних алгоритмов выделения границ, который вычисляет сумму квадратов разниц между диагонально смежными пикселами. Это может быть выполнено сверткой изображения с двумя ядрами:
(2.16)
Оператор Робертса всё ещё используется ради быстроты вычислений, но он проигрывает в сравнении с альтернативами с его значительной проблемой чувствительности к шуму. Он даёт линии тоньше, чем другие методы выделения границ. Иногда его называют «фильтром Робертса».
Оператор Собела
Оператор Собела используется в области обработки изображений. Часто его применяют в алгоритмах выделения границ. По сути, это дискретный дифференциальный оператор, вычисляющий приближенное значение градиента яркости изображения. Используемая им аппроксимация градиента достаточно грубая, особенно это сказывается на высокочастотных колебаниях изображения.
Строго говоря, оператор использует ядра 3×3, с которыми свёртывают исходное изображение для вычисления приближенных значений производных по горизонтали и по вертикали. Пусть A исходное изображение, а Gx и Gy — два изображения, где каждая точка содержит приближенные производные по x и по y. Они вычисляются следующим образом:
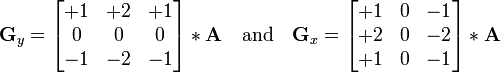(2.17)
где * обозначает двумерную операцию свертки.
Разностный оператор
В результате применения разностных операторов получается, как правило, изображение со средним значением пикселя близким к нулю (сумма элементов ядра равна нулю). Вертикальным перепадам (границам) исходного изображения соответствуют пиксели с большими по модулю значениями на результирующем изображении. Поэтому разностные фильтры называют также фильтрами, находящими границы.
Свертка изображений происходит с двумя ядрами:
(2.18)
Для разных частей изображения приемлемый результат обычно получается при существенно разных пороговых значениях. Кроме того, разностные фильтры очень чувствительны к шумам изображения.
2.4 Метод описания контура объекта
Цепное кодирование является широко известным способом описания границы дискретного объекта. На изображение, содержащее кривую линию, наносится сетка, и фиксируются узлы, ближайшие к пересечению с кривой. Затем последовательность узлов кодируется восьмеричными числами в соответствии с кодом Фримена. Цепным кодом (кодом Фримена) называют последовательность целых чисел от 0 до 7, задающих одно из семи дискретных направлений при переходе от одной граничной точки к следующей при выбранном направлении обхода границы. Граница при этом понимается как замкнутая цепочка в смысле восьми соседей. Этот метод особенно удобен при сравнении двух кривых. Если две кривые идентичны, то функция взаимной корреляции достигает значения 1.
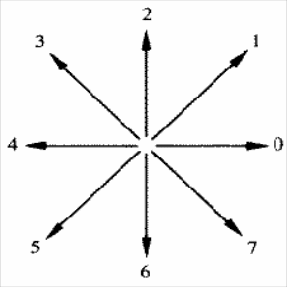
Рисунок 1 – Код Фримена