10.Екінші ретті қисықтар:

1. Эллипс. Фокустар деп аталатын берілген екі нүктеден қашықтықтарыньң қосындысы әрқашанда тұрақты шама болатын жазықтықтағы нұктелердің геометриялык орындарын эллипс деп атайды (9-сызба). Анықтама бойынша F₁M + F₂M = 2a

нүктелер,

М{х, у) -эллипстің бойындағы кез келген жылжымалы нүкте,

2а-тұрақты шама

Егер F₁F₂ = 2с десек, онда F₁(-C;0), F₂(C;0). Сонда:

Енді осы мәндерді қойсақ:

Немесе

Егер а>с болса, онда а² —с²=b² болады. Сондықтан эллипстің канондық теңдеуі деп аталатын теңдеуге келеміз:

Мұндағы х пен у эллипстің кез келген жылжымалы нүктесінің координаттары, а -эллипстің үлкен жарты oci, b -онын кіші жарты oci.

Осьтер эллипске симметриялы, ал симметриялы осьтердің қиылысатын нуктесі эллипстің цeнтpi болады.

қатынасын эллипстің эсцентриситеті деп атайды және оны 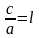деп белгілейді. Сонымен 6ipгe а > с болғандьқтан l < 1 немесе

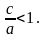
Эллипстің үлкен осіне перпендикуляр тузулердің ішінде 6ip түзудің эллипстің кші осінен қашықтықты d әрқашанда а/l қатынасына тең тұрақты шама болса, онда мұндай тузуді эллипстің директрисасы деп атайды. Директрисалардың тендеу . Эллипс үшін l < 1 болғандьқтан .

Сондықтан эллипстің дериктрисалары оның сыртында жатады.

Егер a=b болса, онда шеңбер эллипстің дерпбес жағдайы болады. Бұл жағдайда с=0, ендеше шеңбердің эксцентриситеті нөлге тең.

3. Гипербола. Фокустар деп аталатын берілген екі нүктеден қашықтықтарының айырмасы әрқашанда тұрақты шама болатын жазықтыктағы нүктелердің геометриялық орындарын гипербола деп атайды.

5.Парабола. Фокус деп аталатын

берілген нүктеден және

директриса деп аталатын берілген

түзуден ара қашықтықтары бірдей болатын жазықтықтарды нүктелерің геометриялык орындарын

парабола дейді Берілген F нүктесінің координаталарын былай белгілейді

Координаталардың бас нүктесінен Р/2 қашықтықтағы ординат осіне параллель берілген

тузуді параболаның директрисасы дейді.

М(х,у) - параболаның бойындағы кез келген жылжымалы нүкте.

Анықтама бойынша

FM=ME

Екі нүктенің ара қашықтыгыньң формуласы бойынша

осы мәндерді апарып қойып, шыққан өрнекті түрлендірсек, параболаның канондық теңдеуі шығады:

у²=2рх

мұндагы р -берілген фокус пен директрисаның арасындағы қашықтық, х пен у - параболаның бойындағы кез келген жылжымалы нуктенің координатасы.

Параболаның эксцентриситеті:

_{Параболаның директрисасының теңдеуі:}

11. Вектордың векторлық көбейтіндісі.

R сызықты кеңістіктің векторлары x, y, z, …, u болсын. Мынадай

v= x+ y+ z+…+ u

теңдікпен анықталған v векторы осы кеңістікте жатады, мұндағы -нақты сандар. Осы v векторды x, y, z, …, u векторларының сызықты комбинациясы деп атайды.

Айталық x, y, z, …, u векторларының сызықты комбинациясы 0 ноль вектор болсын, яғни

x+ y+ z+…+ u= 0. (1)

Анықтама. (1) теңдік барлық = = =…= =0 болған кезде ғана орындалса х, y, z, …, u векторлары сызықты тәуелсіз деп аталады. Ал егер (1) теңдік , , ,…, сандарының ең болмағанда біреуі нолден өзгеше болғанда орындалса х, y, z, …, u векторлары сызықты тәуелді деп аталады.

Мынадай тұжырымның дұрыстығына көз жеткізу қиын емес: Егер x, y, z, …, u векторлар сызықты тәуелді болса, онда бұл векторлардың біреуі басқаларының сызықты комбинациясы арқылы жіктеледі. Және керісінше, егер x, y, z, …, u векторлардың біреуі басқаларының сызықты комбинациясы арқылы жіктелсе, онда бұл векторлар сызықты тәуелді болады.

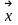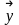Жазықтықтағы коллинеар емес екі вектор сызықты тәуелсіз векторға мысал болады. Шынында да, жазықтықтағы және векторлары үшін (1) теңдік

+ =0

тек = =0 болғанда ғана орындалады. Ал, олай демесек, мысалы болса, онда =- болып, пен векторларының коллинеарлығын білдірген болар еді. Ал бірақ жазықтықтағы кез келген үш вектор сызықты тәуелді болады.

Векторлық кеңістіктің қасиеттері:

1. Егер x, y, z, …, u векторларының ішінде ноль-вектор бар болса, онда бұл векторлар сызықты тәуелді болады. Шынында да, егер, мысалы, x=0 болса, онда (1) теңдік

=1, = =…= =0 болғанда орындалады.

2. Егер x, y, z, …, u векторларының қандай да бір бөлігі сызықты тәуелді болса, онда бұл векторлардың бәрі сызықты тәуелді болады. Шынында да, мысалы, y, z, …, u векторлары сызықты тәуелді болсын десек y+ z+…+ u=0 теңдік , ,…, сандарының бәрі бір мезгілде нолге тең болмағанда орындалып тұр деген сөз. Олай болса бұл теңдік сол , ,…, сандары және =0 санымен де орындалады.

Мысал қарастырайық. x=(3,2,-1), y=(2,-1,3), z=(1,3,-4) векторлары сызықты тәуелді ме ?

Шешуі. x, y, z векторлары сызықты тәуелді болады, егер

x+ y+ z= 0

теңдігі , , сандарының ең болмағанда біреуі нолден өзгеше болғанда орындалса. x, y, z векторларын бағана түрінде жазып, теңдікті ашып жазайық:

+ + = 0

Есеп мынадай жүйені шешуге келтірілді:

Жүйе біртекті, яғни оның нолдік шешімі әруақытта бар. Жүйені Гаусс әдісімен шешіп жүйенің нолдік емес шексіз көп шешімін табуға болады:

, ,

мұндағы С-ерікті нақты сан.

Сонымен, берілген векторлар үшін (1) теңдік , , сандарының ең болмағанда біреуі нолден өзгеше болғанда (айталық, , (С=1)) орындалып тұр, олай болса берілген векторлар сызықты тәуелді.

Анықтама. Егер R сызықты кеңістікте n сызықты тәуелсіз вектор бар болып, ал осы кеңістіктің кез келген n+1 векторы сызықты тәуелді болса, онда R кеңістікті n өлшемді деп атайды. Кейде кеңістік өлшемі n-ге тең дейді де, dim(R)=n деп немесе Rⁿ деп жазады.

Анықтама. п өлшемді векторлық кеңістіктің п сызықты тәуелсіз векторларының жиыны базис деп аталады.

Мынадай тұжырымдар дұрыс болады: