9.Жазықтықтағы түзу теңдеулері.

1)Түзулердің теңдеулері

Жазықтықтағы түзу (1-сурет) Оу осін В(0;b) нүктесінде қиып, Ох осімен (0< < ) бұрыш жасасын. Түзу бойынан қандай да бір М(х,у) нүкте алайық. Түзудің Ох осімен жасаған бұрышының тангенсін ВМК үшбұрышынан табамыз:

(1)

деп белгілеп, түзудің бұрыштық коэффициенті деп атау қабылданған. Сонымен:

.

Осы қатынастан у-ті тапсақ:

y=kx+b (2)

Түзу бойында жатқан кез келген нүктенің координатасы (2) теңдеуді қанағаттандырады да түзуден тыс жатқан нүктелер бұл теңдеуді қанағаттандырмайды.

(2) теңдеу түзудің бұрыштық коэффициентімен берілген теңдеуі деп аталады.

Дербес жағдайларын қарастырайық.

1. Түзудің бұрыштық коэффициентімен берілген теңдеуіндегі b=0 болсын. Онда түзу теңдеуі y=kx түрге келеді де, түзу координат басынан өтеді (2-сурет)

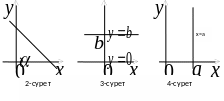2. Егер 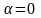болса, онда 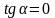болады да, түзу теңдеуі y=b түрге келеді де, түзу Ох осіне параллель болады (3-сурет). Ал Ох осінің теңдеуі y=0 болады.

3. Егер болса, онда мәні болмайды, түзу Ох осіне перпендикуляр болады. Айталық түзу Ох осінен а тең кесінді қиып өтеді, сонда түзу теңдеуі х=а түрде болады (4-сурет). Ал Оу осінің теңдеуі х=0 болады.

Мынадай теорема айтуға болады.

Теорема. Тік бұрышты координаталар жүйесінде кез келген түзу бірінші ретті теңдеумен беріледі

Ах+Ву+С=0 (3)

Және керісінше, (3) теңдеу (А, В, С коэффициенттердің бәрі бір мезгілде нолге тең болмаған кезде) тік бұрышты координаталар жүйесінде қандай да бір түзуді анықтайды.

(3) теңдеуді әдетте түзудің жалпы теңдеуі деп атайды.

Берілген бағыт және берілген нүкте арқылы өткен түзу теңдеуі. Көп жағдайда түзу теңдеуін оның бойында жатқан белгілі нүкте мен k бұрыштық коэффициенті арқылы жазу керек болады (5-сурет).

Түзу теңдеуін (2) түрінде жазайық, y=kx+b, мұндағы b әзірше белгісіз. Түзу нүктесі арқылы өтетіндіктен, нүкте координатасы түзу теңдеуін қанағаттандыруы керек: y₁=kx₁+b. Осы теңдіктен белгісіз b табылады, b = y₁ - kx_1. Табылған мәнді теңдеудегі орнына қойып, берілген бағыт және берілген нүкте арқылы өткен түзу теңдеуін аламыз:

y =k(x – x₁)+ y₁ (4)

Егер (4) теңдеудегі k ерікті мән қабылдаса, онда теңдеу нүктесі арқылы өтетін түзулер шоғының теңдеуін анықтайды (6-сурет).

Берілген екі нүкте арқылы өткен түзу теңдеуі. және нүктелері берілсін. АВ түзуінің теңдеуін жазу үшін А нүктесі арқылы өткен түзулер шоғының теңдеуін жазамыз:

y =k(x – x₁)+ y_1.

АВ түзуі нүктесі арқылы өтетіндіктен, нүкте координатасы түзу теңдеуін қанағаттандыруы керек: y₂ =k(x₂ – x₁)+ y_1. Осы теңдіктен белгісіз k табылады, . Табылған мәнді теңдеудегі орнына қойып, берілген екі нүкте арқылы өткен түзу теңдеуін аламыз:

(5)

Т үзудің «кесіндідегі» теңдеуі. Түзу Ох осінен а-ға тең, Оу осінен b-ға тең кесінді қиып өтсін (8-сурет). Түзу А(а;0) және В(0;b) нүктелері арқылы өтеді деп, (5) теңдеуді қолданайық. Сонда түзу теңдеуі мынадай түрде жазылады:

Енді ықшамдасақ, түзудің “кесіндідегі” теңдеуін аламыз:

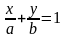(6)

Екі түзу арасындағы бұрыш. Екі түзу берілсін: y=k₁x+b₁, y=k₂x+b₂. Мұндағы , . Екі түзу арасындағы бұрышты табу керек (9-сурет).

С уреттен көрініп тұрғандай . Осыдан

немесе

(7)

(7) формула берілген екі түзу арасындағы бұрышты анықтайды. Ал екінші бұрыш тең болады.

Екі түзудің параллелдік және перпендикулярлық шарты. Егер екі түзу параллель болса, онда =0 болады да tg =0. Бұл жағдайда (7) формула мынадай түрге келеді: k₂ – k₁ = 0. Осыдан екі түзудің параллелдік шарты шығады:

k₂ = k₁ , (8)

яғни екі түзудің бұрыштық коэффициенттері тең болса, ол түзулер параллель болады және керісінше.

Егер екі түзу перпендикуляр болса, онда болады да, , . Осыдан екі түзудің перпендикулярлық шарты шығады:

k₂ = , (9)

яғни екі түзудің бұрыштық коэффициенттері мәндері бойынша кері, таңбалары бойынша қарама-қарсы болса, ол түзулер перпендикуляр болады және керісінше.