15. Функция дифференциалы.

А)ФУНКЦИЯ ДИФФЕРЕНЦИАЛЫ

Функция шегінің анықтамасына сүйеніп туынды табу формуласын мынадай түрде көшіріп жазуға болады: ,

мұндағы - ақырсыз аз шама, яғни . Түрлендірейік,

,

мұндағы - функция өсімшесінің сызықты бөлігі деп аталады және ол өсімшеге пропорционал. Ал шама екі ақырсыз аздың көбейтіндісі ретінде өсімшеге қарағанда жоғары ретті ақырсыз аз шама болады.

Анықтама. Функция өсімшесінің сызықты бөлігі функция дифференциалы деп аталады да, dy деп белгіленеді. Сонымен,

y=x функциясының дифференциалын табайық: . Демек аргумент дифференциалы оның өсімшесіне тең екен. Олай болса функция дифференциалын мынадай түрде жазамыз:

(4)

Егер аргумент өсімшесі абсолют шамасы бойынша аз шама болса, онда функция өсімшесі мен дифференциалы жуық шамамаен тең болады, яғни . Түрлендірейік, . Осыдан,

(5).

(5) формуламен функцияның мәнін жуықтап есептейді. Неғұрлым аз болса, соғұрлым формула дәлірек болады.

В)Дифференциалдау ережелері. u=u(x) және v=v(x) функциялардың әрқайсысы берілгенх нүктесінде дифференциалданатын болса, онда бұл функциялардың қосындысы(айырымы), көбейтіндісі және қатынасы (v(x) 0) сол нүктеде дифференциалданады, және мына формулалар дұрыс болады:

1)

2) , C=const

3)

4) .

5. f(u(x)) күрделі функция туындысы:

.

5. y=f(x) функциясына кері функция (x=f ^{- 1}(y)) туындысы:

.

5. Айқын емес түрде берілген функция, F(x,y)=0, туындысы:

.

5. Дәрежелі-көрсеткіштік функция туындысы. Алдымен берілген теңдеудің екі жағын логарифмдейік,

.

Екі жағынан туынды аламыз,

.

Сонымен,

9) Жоғары ретті туынды. туындыны функцияның 1-ретті туындысы дейді. 1-ретті туындыдан алынған туынды функцияның 2-ретті туындысы деп аталады да, деп белгіленеді. Сонымен,

.

Осылайша 3-ретті, т.с.с. n–ретті туындыларды анықтауға болады,

, …, .

Анықтама. функциясы нүктесінде дифференциалданады, егер оның осы нүктеде дифференциалы болса.

Егер функциясы дифференциалданатын болса, онда ол міндетті түрде үзіліссіз болады.

Дифференциалды жуықтап есептеулерге пайдалану.

. Соңғы жуықталған теңдік ең алдымен тәжірибелік тұрғыдан қарағанда келесі есепті шешу үшін қолданады: мәндері белгілі; -тің жуық мәнін есептеу керек. Сонда төменгі формула анықталады: .

Мысалы: мәнін табу керек: , , , демек . Ал , . Сонда .

16. Функцияның нүктедегі үзіліссіздігі.Функцияның үзіліс нүктелері

А)Функцияның үзіліссіздігі.Анықтама. функциясының жағдайда шегі функцияның сол нүктедегі мәніне тең болса, яғни , функция нүктесінде үзіліссіз деп аталады. Егер .

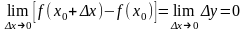Сонда функция үзіліссіздігінің анықтамасын былай да айтуға болады: Берілген нүктеде аргументтің ақырсыз аз өсімшесіне функцияның да ақырсыз аз өсімшесі сәйкес келсе, яғни функция нүктесінде үзіліссіз деп аталады. функциясы қандай да бір аралықтың үзіліссіз болуы үшін, ол сол аралықтың әрбір нүктесінде үзіліссіз болуы керек.

Үзіліссіз функция қасиеттері.

1. функциясы нүктесінде үзіліссіз, ал функциясы нүктесінде үзіліссіз болса, күрделі функциясы нүктесінде үзіліссіз болады және

.

2.Нүктеде үзіліссіз функциялардың алгебралық қосындысы, көбейтіндісі және қатынасы (бөліміндегі функция нолден өзге болғанда) үзіліссіз функция болады.

Б)Үзіліс нүктелерінің түрлері. Анықтама. функциясының жағдайда шегі функцияның сол нүктедегі мәніне тең болмаса, яғни , функция нүктесінде үзілісті функция деп, ал нүктені функцияның үзіліс нүктесі деп атайды.

Біржақты шектер ұғымын енгізейік.

Айталық және , онда деп жазады, ал осы жағдайдағы шекті функцияның сол жақты шегі деп атайды. Дәл осылайша функцияның оң жақты шегі де анықталады. Функцияның сол жақты және оң жақты шектерін біржақты шектер дейді.

Анықтама. Функцияның нүктесінде өз-ара тең емес ақырлы біржақты шектері бар болса, нүктесі функцияның І-текті үзіліс нүктесі деп аталады. Кейде оны ақырлы секіріс деп (10а-сурет) атайды.

Анықтама. Функцияның нүктесіндегі ақырлы біржақты шектердің ең болмағанда біреуі жоқ болса, нүктесі функцияның ІІ-текті үзіліс нүктесі деп аталады (10б-сурет).

Мысал. а) функциясы нүктесінде үзіліссіздікке зертте.

Шешуі.

, яғни сол жақты шегі –1, ал оң жақты шегі 1, ақырлы сандар, өз-ара тең емес, олай болса нүктесі І-текті үзіліс нүктесі болады (10а-сурет).