- •Построить точку пересечения прямой а с плоскостью α, определить видимость.
- •Определить истинную величину отрезка ав.
- •Найти величину перпендикуляра, опущенного из точки м на плоскость авс.
- •Построить третью (профильную) проекцию пирамиды. Найти точку n на горизонтальной, профильной проекциях и в аксонометрической проекции пирамиды.
- •Определить расстояние между параллельными прямыми.
- •6. Построить точку пересечения прямой l с плоскостью abc, определить видимость.
- •7. Определить какой из отрезков длиннее.
- •8. Способом замены плоскостей проекций определить истинную величину треугольника авс.
- •9.Построить сечение пирамиды плоскостью, заданной двумя пересекающимися прямыми. Найти его натуральную величину.
- •10. Определить точки пересечения прямой l с конусом.
- •11.Построить сечение конуса и цилиндра, определить видимость.
- •12.Построить точку пересечения прямой а с плоскостью α, определить видимость.
- •13.Достроить горизонтальную проекцию многоугольника авсde и найти его натуральную величину.
- •14. Найти величину перпендикуляра, опущенного из точки м на плоскость авс.
- •15. Построить три проекции точек, заданных координатами: а (-30; 10;20), в (40;20;15), с (20; -40; 15)
- •16. Построить линию пересечения призмы и конуса.
- •17. Построить линию пересечения двух плоскостей, определить видимость линий.
- •18. Построить точку пересечения прямой l с плоскостью abc, определить видимость.
- •19. Построить вторую проекцию прямой, принадлежащей плоскости α.
- •21.Построить три проекции точек, заданных координатами: а (-40; -10;20), в (40;20;-60), с (20; 40; 15)
- •22. Построить призму sabc в аксонометрической проекции.
- •23. Построить сечение способом концентрических сфер.
- •29.Определить точку пересечения l с плоскостью, заданной прямыми ав и ас.
- •30.Построить вторую проекцию плоского четырехугольника, если даны три точки, принадлежащие его плоскости.
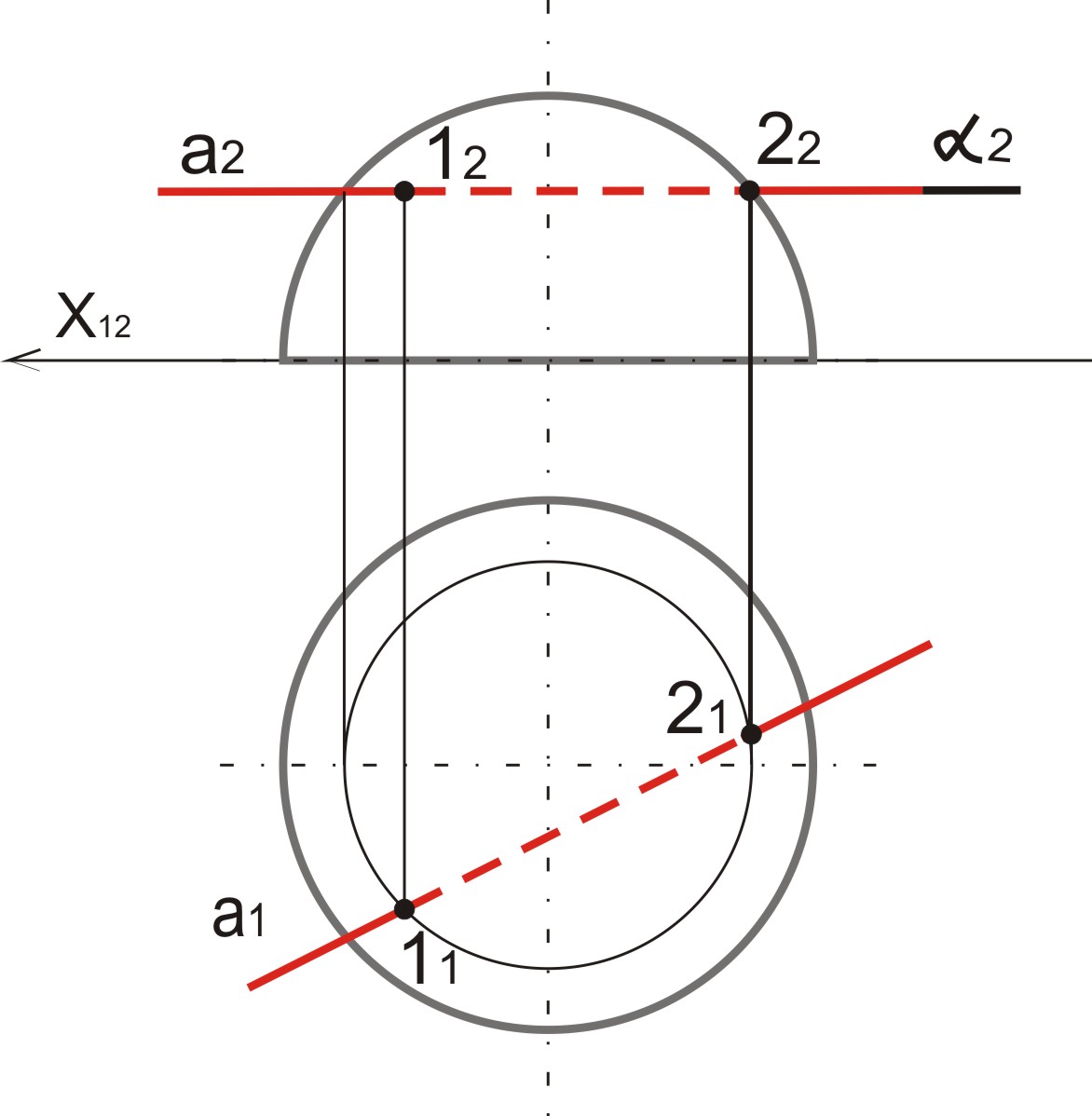
- •39. Построить точки пересечения полусферы с прямой а, показать видимость.
- •40.Определить расстояние от т. А до плоскости mnk.
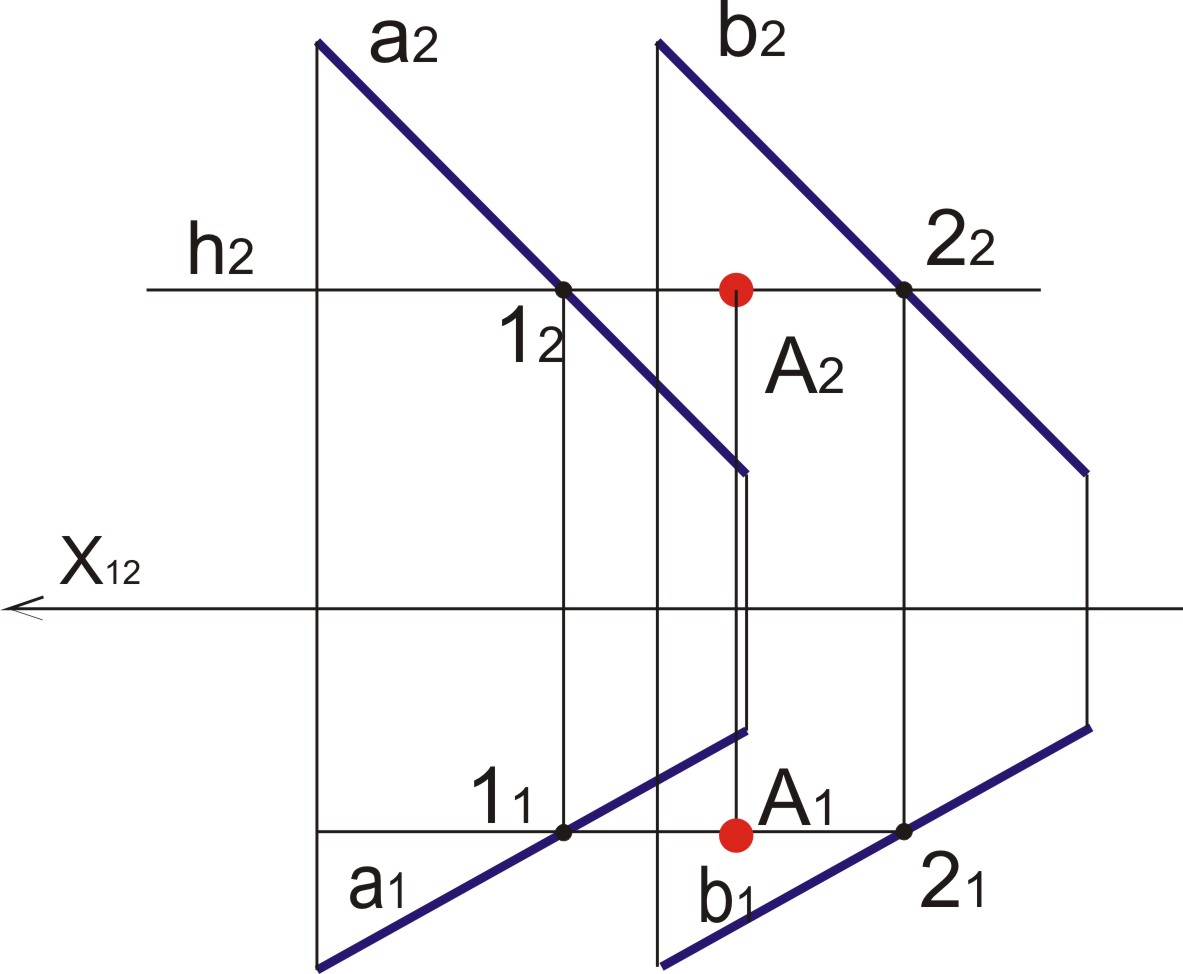
- •42 .Построить точку пересечения прямой с с плоскостью, заданной пересекающимися прямыми а и b.
- •43. Построить три проекции точек, заданных координатами: а (35; -10;-20), в (30;20;60), с (-20; -40; -15)
- •45. Построить проекции точки а, которая принадлежит плоскости β общего положения, заданной параллельными прямыми а и b.
- •46. Построить линию пересечения плоскости, заданной пересекающимися прямыми a и b и прямыми с и d.
- •47. Построить линию взаимного пересечения поверхностей, определить видимость.
- •48. Построить точку пересечения прямой с и плоскости, заданной параллельными прямыми а и b.
- •49. Построить фронтальную проекцию кривой m, принадлежащей плоскости α.
- •50. Способом замены плоскостей проекций определить истинную величину фигуры.
- •51. Определить расстояние от точки d до плоскости, заданной ∆авс.
- •52. Построить точки пересечения прямой со сферой.
- •53. Построить линию пересечения конуса и полусферы, определить видимость.
- •61. Построить горизонтальную проекцию точки а, которая принадлежит плоскости, заданной прямой bc и точкой в.
- •63. Определить линию пересечения плоскостей, заданных пересекающимися прямыми с и d и а и b
- •64.Построить линию пересечения цилиндра и шара.
- •65. Построить точку пересечения прямой l с плоскостью abc, определить видимость.
- •66. Построить три проекции прямой а (50; 15;50), в (20;30;0), найти его натуральную величину
- •71. Построить недостающую проекцию треугольника, лежащего в плоскости, заданной параллельными прямыми а и b
- •72. Вращением вокруг оси I совместить точку k с плоскостью α
- •73. Построить линии пересечения цилиндра с конусом
- •74. Построить линию пересечения двух плоскостей, определить видимость линий
- •75. Построить точку пересечения прямой с с плоскостью, заданной пересекающимися прямыми а и b
- •76. Построить три проекции прямой а (0; 5;50), в (10;30; 0), найти его натуральную величину
- •77. Построить недостающую проекцию треугольника, лежащего в плоскости, заданной параллельными прямыми a и b.
- •78. Преобразовать чертеж так, чтобы отрезок ав спроецировался в точку (применить способ замены плоскостей проекций).
- •79. Построить линию пересечения призмы и конуса
- •80.Построить линию пересечения пирамиды с плоскостью
- •81. Построить точку пересечения прямой а с плоскостью α.
- •82. Построить три проекции прямой а (40; 5;50), в (20;30; 0), найти его натуральную величину
- •83. Построить три проекции прямых ав и cd общего положения, заданных координатами точек: а (20; -30;-10), в (-20;15;30), с (40; -10; 15), d (15;-30;-35).
- •84. Определить расстояние от т. А до плоскости cde
- •85.Построить через точку а прямую, перпендикулярную прямой b.
- •86. Построить сечение конуса и цилиндра, определить видимость.
39. Построить точки пересечения полусферы с прямой а, показать видимость.
а) Через прямую а2 в π2 проводим α2
б) α2∩ с полусферой по ее образующей
в) Находим проекции точек в π1 на горизонтальной оси полусферы и проводим окружность данным радиусом
г) Окружность пересекает прямую I в точках 1121, находим их проекции в π2
д) Определяем видимость
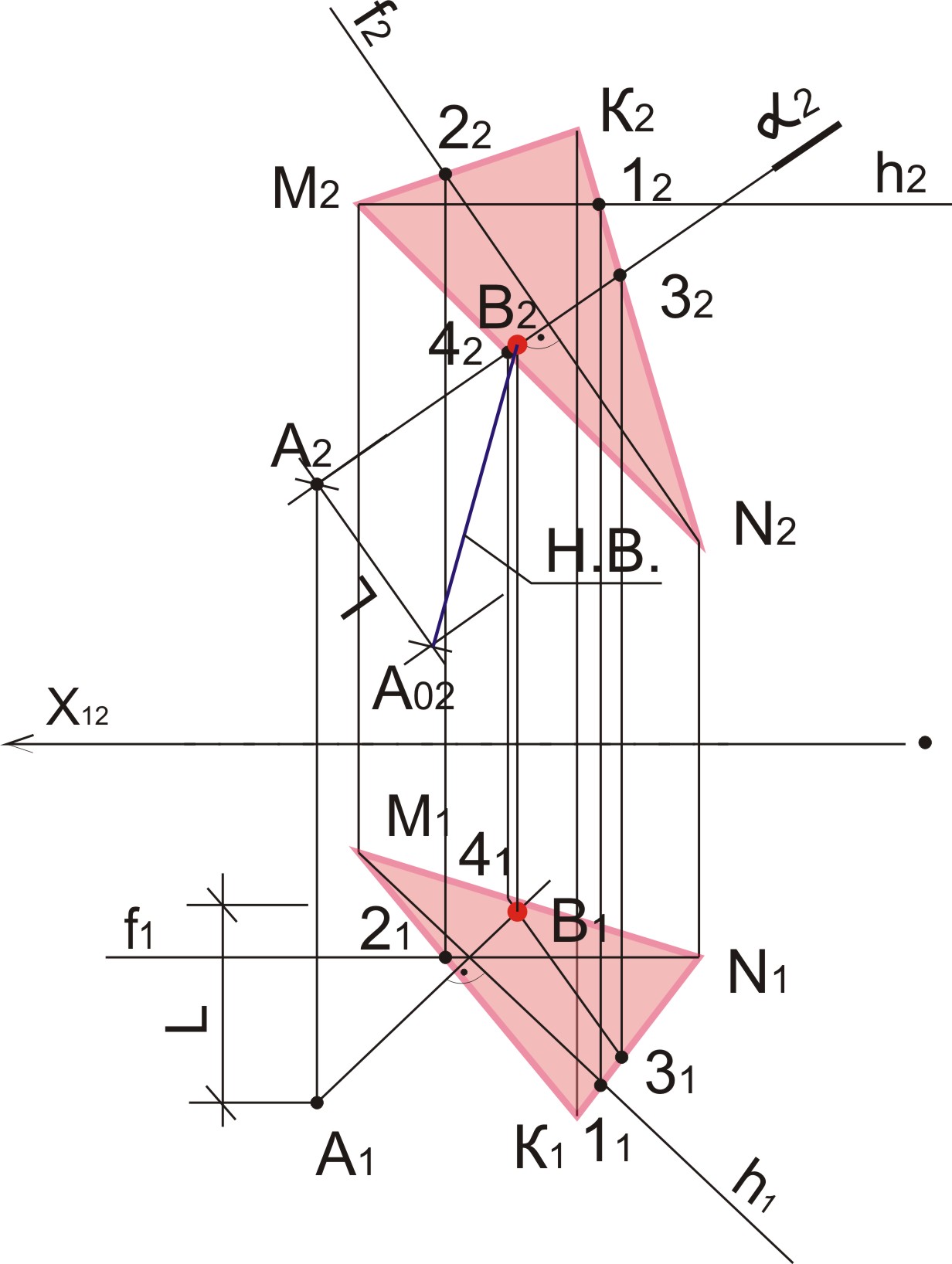
40.Определить расстояние от т. А до плоскости mnk.
а) Проводим в π2 горизонталь h2 II оси х, замечаем точку 12, находим ее проекцию 11 в π1, проводим h1
б) Проводим в π1фронталь f1 II оси х, замечаем точку 21, находим ее проекцию 22 в π2, проводим f2
в) Опускаем перпендикуляр из т. А2 на f2
г) Опускаем перпендикуляр из т. А1 на h1
д) Заключаем перпендикуляр из т. А2 в плоскость α2
е) Плоскость α2 ∩ (MKN) = 32 42, находим их проекции в плоскости π1
ж) Перпендикуляр, опущенный из т. А пересекается с 31 41 в т. В1 , находим проекцию т. В в π2
з) Находим длину АВ, для этого в π1 замечаем длину перпендикуляра
А2 В2 = L (измерения производить перпендикулярно оси х)
и) В π2 перпендикулярно А2 В2 из т. А2 выводим перпендикуляр и откладываем длину L, получаем т. А02; длина В1 А01 – истинная величина перпендикуляра АВ.
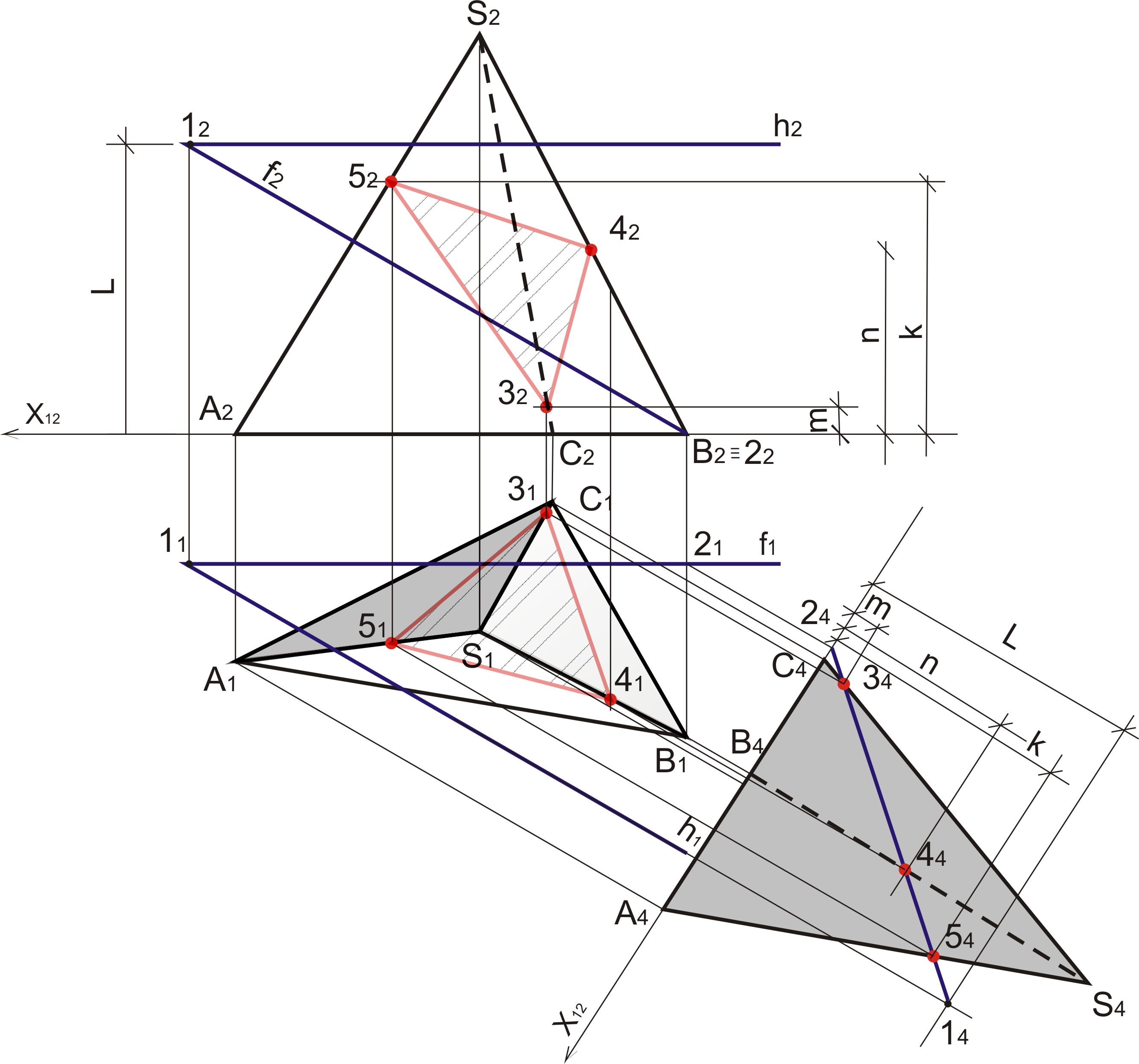
41. Построить сечение пирамиды плоскостью, заданной фронталью и горизонталью.
а) В плоскости π1 перпендикулярно h1 производим замену плоскости проекций π4; сносим проекции точек пирамиды и плоскости (h∩f)
б) Плоскость (h∩f) занимает в π4 проецирующее положение, она пересекает SAВС в точках 24 , 34 , 4 4, 54; находим их проекции в π1 и π2
в) Соединяем полученные точки получаем сечение 22 32 42 5 2
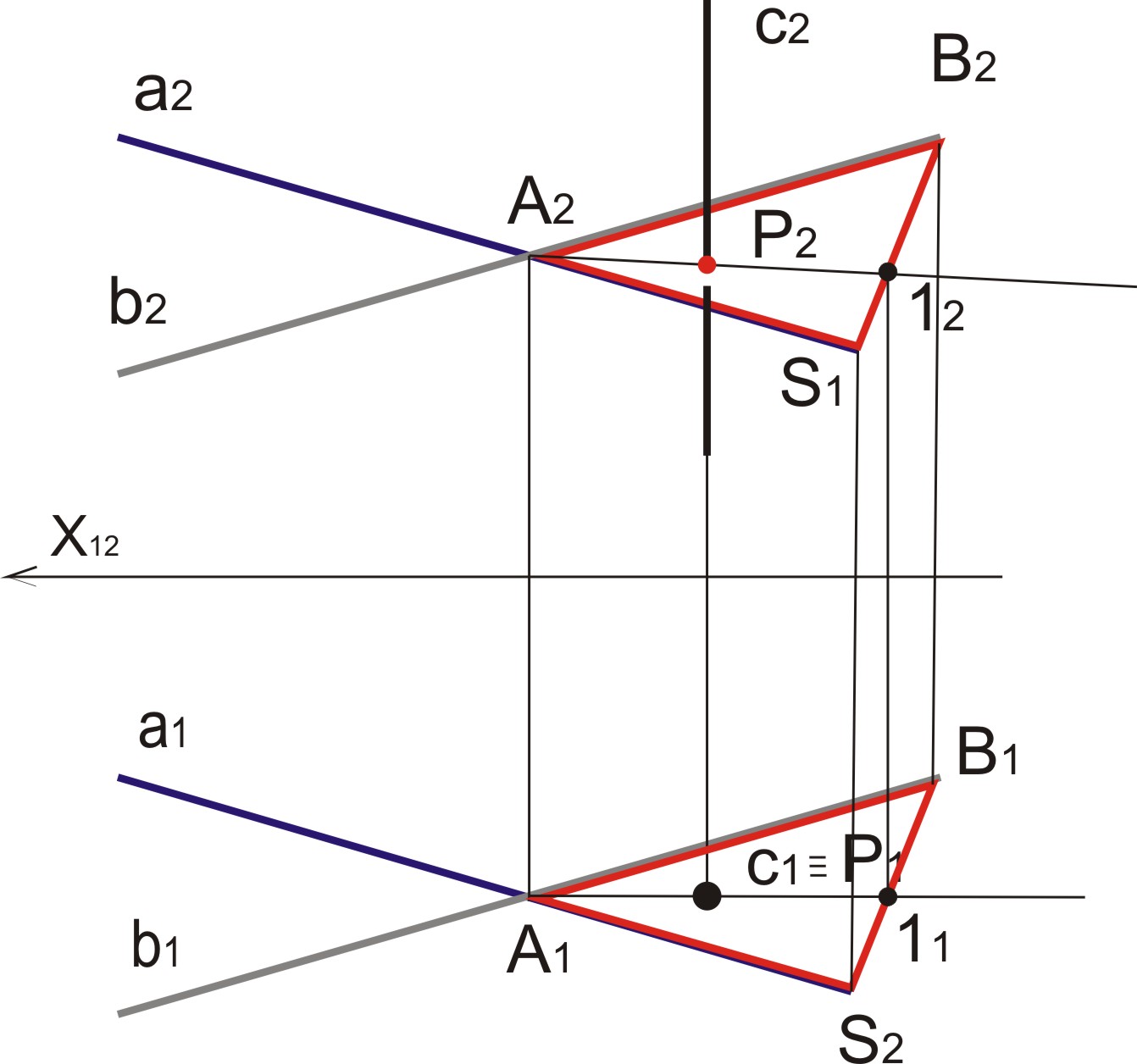
42 .Построить точку пересечения прямой с с плоскостью, заданной пересекающимися прямыми а и b.
а) В плоскости π1через прямую проводим плоскость α1, она засекает плоскость (a ∩ b) (ABS) в точках 1121, находим их проекции в π2
б) 1222∩ с2 =Р2 – точка пересечения прямой с и (a ∩ b)
43. Построить три проекции точек, заданных координатами: а (35; -10;-20), в (30;20;60), с (-20; -40; -15)
а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;
б) Каждая точка должна иметь три проекции.
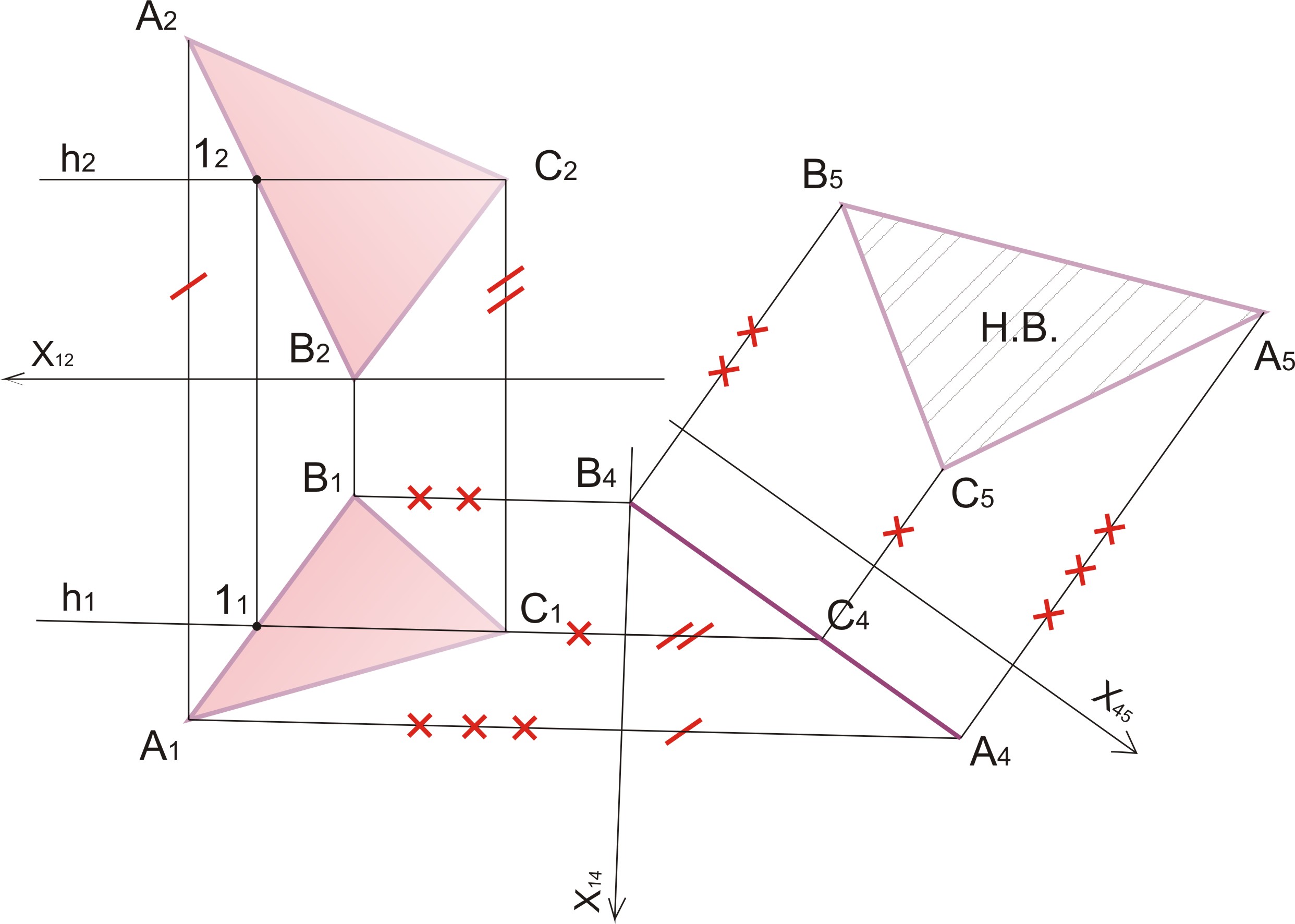
44. Способом замены плоскостей проекций определить истинную величину треугольника АВС.
а) Проводим из т. С2 горизонталь h2 II оси х, на АВ замечаем т. 12, проецируем ее в π1, находим т. 11 на А1 В1
б) Перпендикулярно h1 в проекции С производим замену плоскости проекций π4
в) Проецируем точки АВС на π4 перпендикулярно оси х14 и отмечаем проекции точек согласно высотам в плоскости π2 соответственных точек
г) II А4 В4 С4 вводим плоскость π5 и проецируем перпендикулярно оси х45; точки А5 В5 С5, откладываем на расстоянии от точек А1 В1 С1 до х14
д) А5 В5 С5 – натуральная величина плоскости АВС
45. Построить проекции точки а, которая принадлежит плоскости β общего положения, заданной параллельными прямыми а и b.
а)т.к. т. А принадлежит плоскости, заданной (a II b), то через т. А мы можем провести горизонталь h2 в π2; h2∩(a2 II b2)= 1222, находим их проекции в π1
б) из т. А2 опускаем проекционный луч в π1; пересечение луча и 1121 –искомая проекция т. А.