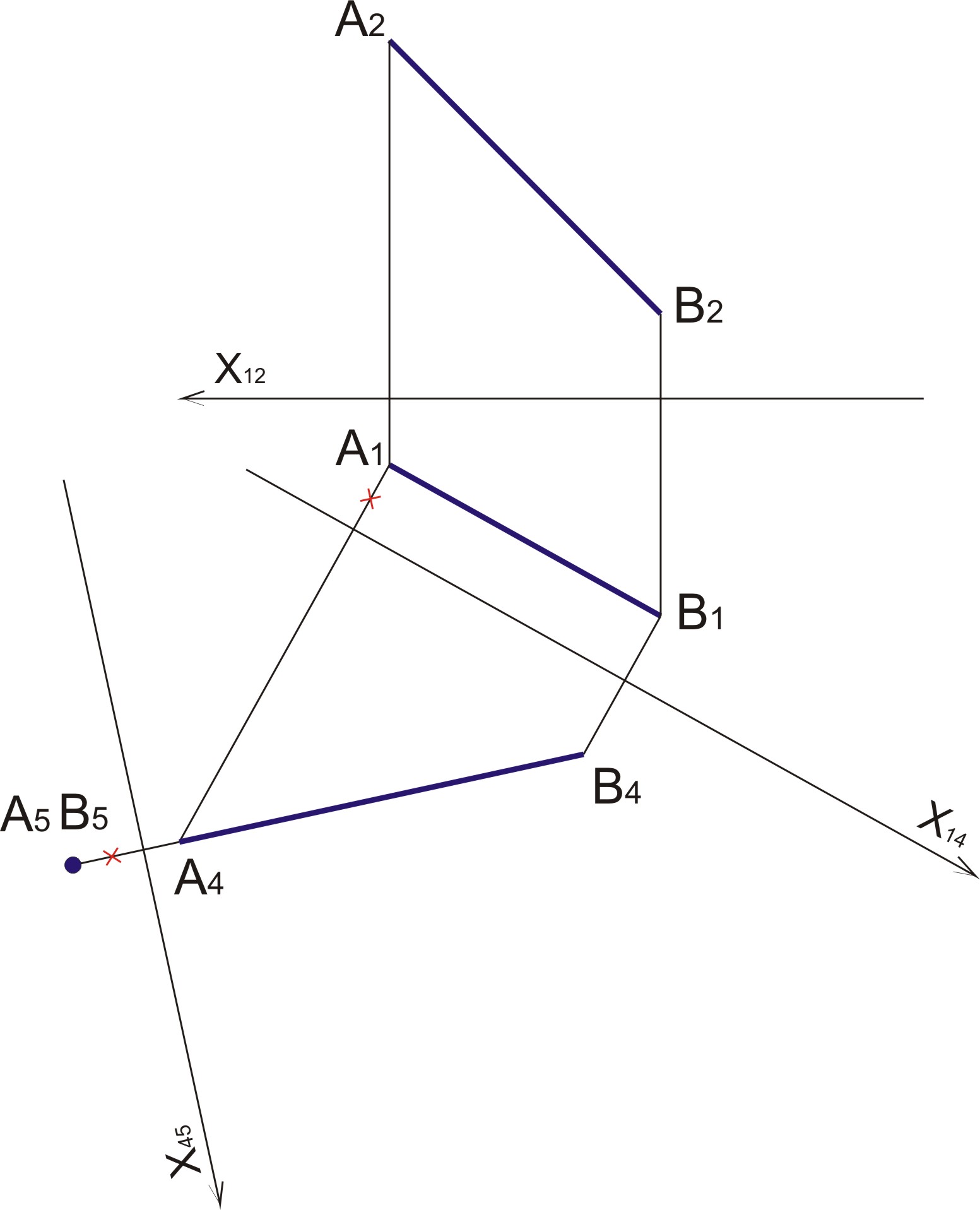
78. Преобразовать чертеж так, чтобы отрезок ав спроецировался в точку (применить способ замены плоскостей проекций).
а) Производим замену плоскости π1 на π4 II А1 В1
б) Находим проекции А4 В4 согласно высотам в плоскости π2
в) Производим замену плоскости π4 на π5 перпендикулярно отрезку А4В4; перпендикулярно оси х45 переносится проекция отрезка, проецирующаяся в точку (расстояния от оси х45 откладываются согласно расстоянию от отрезка до оси х14)
79. Построить линию пересечения призмы и конуса
а) Рассмотрим π1: находим середины сторон призмы: 11, 21, 31 и их проекции во фронтальной плоскости
б) Продливаем прямые S1 31; S1 21;S1 11 до пересечения с основанием конуса в т. 6 1,51,41 соответственно
в) Находим проекции прямых S1 61;S 151; S1 41 в плоскости π2
г) Определяем точки пересечения данных прямых с проекциями середин отрезков призмы
д) Определяем линию пересечения призмы и конуса
е)Определяем видимость
80.Построить линию пересечения пирамиды с плоскостью
а) В плоскости π1 перпендикулярно h1 производим замену плоскости проекций π4; сносим проекции точек пирамиды и плоскости (h∩f)
б) Плоскость (h∩f) занимает в π4 проецирующее положение, она пересекает SAВС в точках 24 , 34 , 4 4, 54; находим их проекции в π1 и π2
в) Соединяем полученные точки получаем сечение 22 32 42 5 2
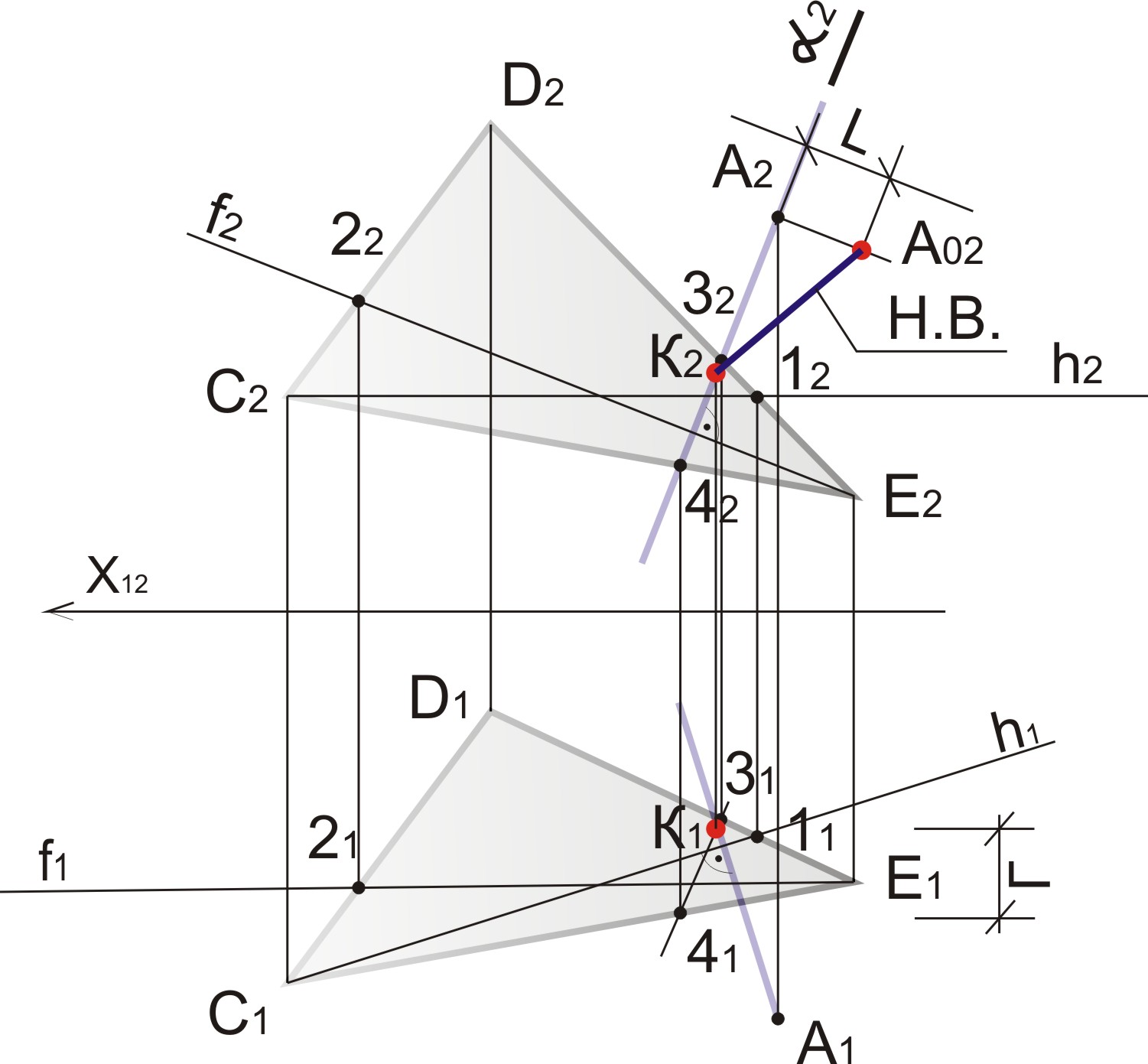
81. Построить точку пересечения прямой а с плоскостью α.
а) Заключаем прямую a в плоскость β; α∩β=12
б) Находим проекцию точки 1 на плоскости π1
в) Проводим прямую а2 до пересечения с осью х, получаем т. 22
г) Находим проекцию т. 2 в плоскости π1
д) Соединяем т. 11 и 21 (11 21) ∩ α = К1
е) Определяем видимость.
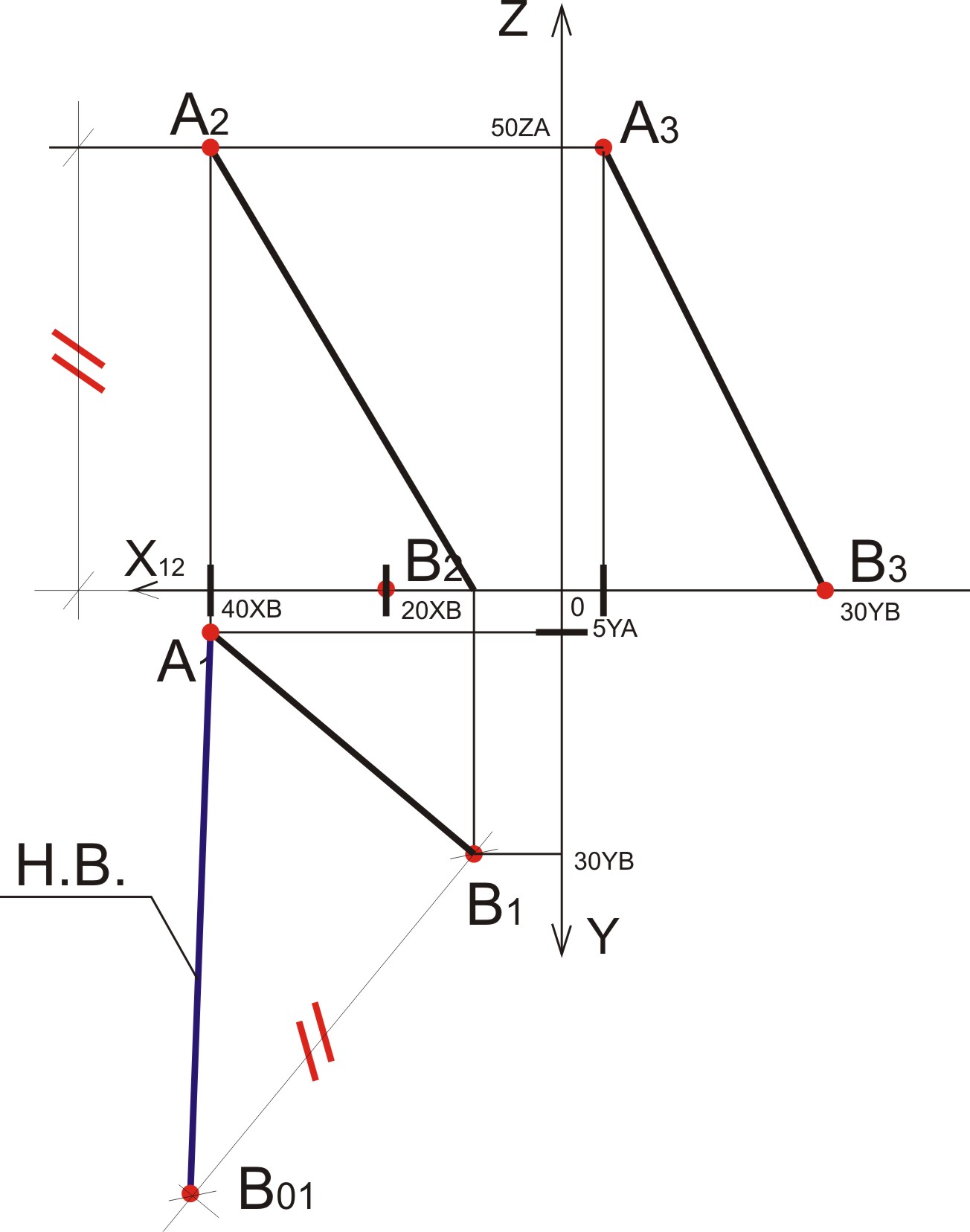
82. Построить три проекции прямой а (40; 5;50), в (20;30; 0), найти его натуральную величину
а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;
б) Находим третью проекцию прямой:
- откладываем значение y по горизонтали с правой стороны от оси z и находим проекции точек согласно фронтальным проекциям точек
в) Находим Н.В.- проводим в π2 из т. В2 горизонталь h2;
- полученное расстояние от т. А2 до h2 откладываем на перпендикуляре от т. В1 в π1;
- В01А1 – натуральная величина.
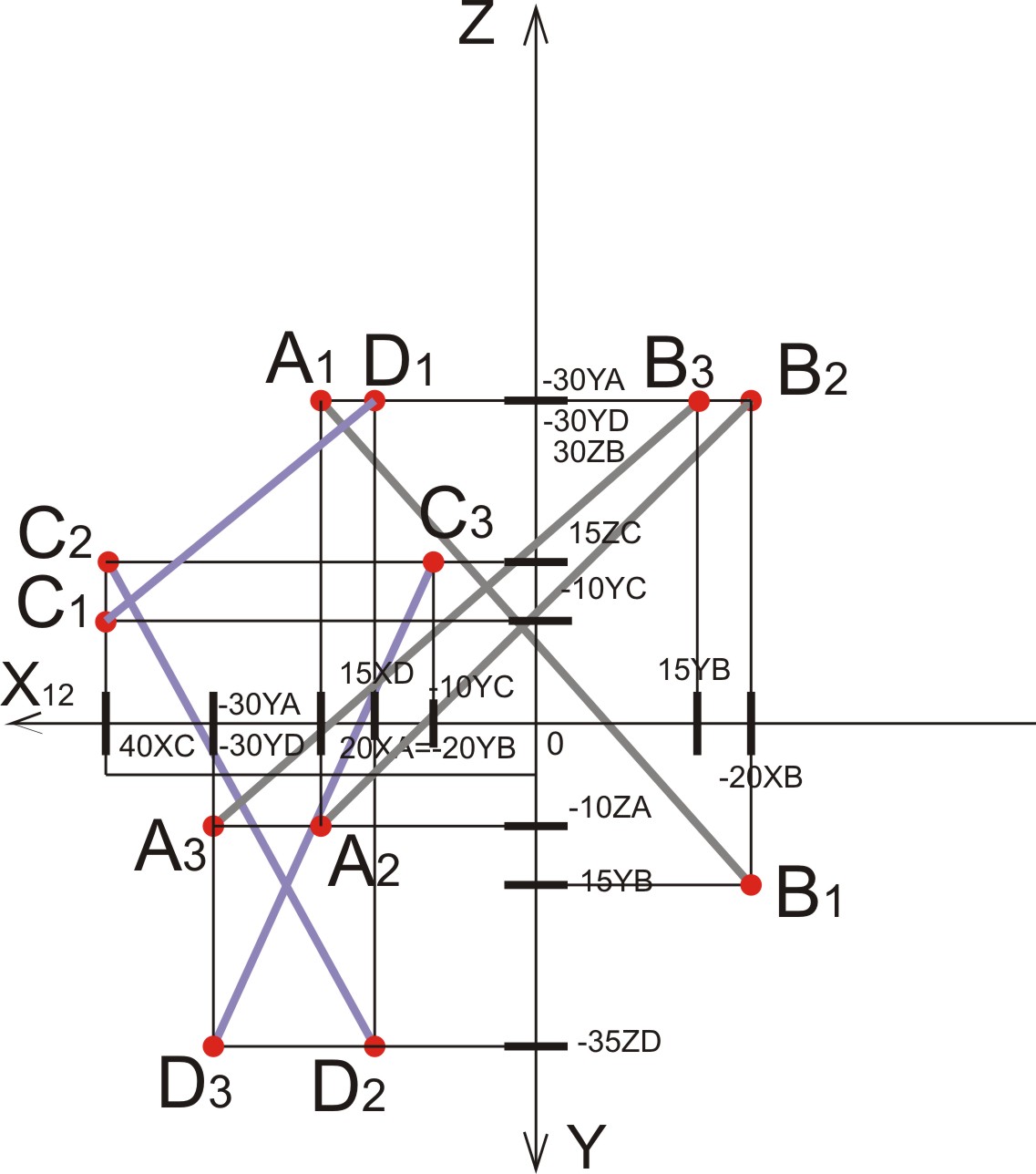
83. Построить три проекции прямых ав и cd общего положения, заданных координатами точек: а (20; -30;-10), в (-20;15;30), с (40; -10; 15), d (15;-30;-35).
а) Согласно заданным координатам откладываем проекции точек в соответствии с установленными направлениями осей;
б) Каждая точка должна иметь три проекции.
в) Соединяем получившиеся проекции прямых А 1В1 и C1 D1, А2 В2 и
C2 D2, А3 В3 и C3 D3
84. Определить расстояние от т. А до плоскости cde
а) Проводим в π2 горизонталь h2 II оси х, замечаем точку 12, находим ее проекцию 11 в π1, проводим h1
б) Проводим в π1фронталь f1 II оси х, замечаем точку 21, находим ее проекцию 22 в π2, проводим f2
в) Опускаем перпендикуляр из т. А2 на f2
г) Опускаем перпендикуляр из т. А1 на h1
д) Заключаем перпендикуляр из т. А2 в плоскость α2
е) Плоскость α2 ∩ (CDE) = 32 42, находим их проекции в плоскости π1
ж) Перпендикуляр, опущенный из т. А пересекается с 31 41 в т. К1 , находим проекцию т. К в π2
з) Находим длину АК, для этого в π1 замечаем длину перпендикуляра
А1 К1 = L (измерения производить перпендикулярно оси х)
и) В π2 перпендикулярно А2 К2 из т. А2 выводим перпендикуляр и откладываем длину L, получаем т. А02; длина К2А02 – истинная величина перпендикуляра А К.
