Билет № 1

1. Взаимное положение точки и прямой

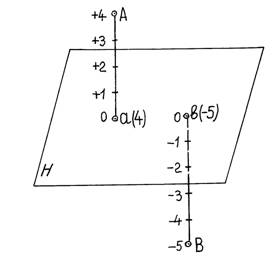
Числовой отметкой называется расстояние по нормали от проектируемых точек до плоскости проекции Н. За основную плоскость проекции может быть принята любая, чаще всего горизонтальная плоскость. Если точка расположена выше или вправо от плоскости проекции (п.п.), то расстояние считается положительным и отметка ставится со знаком плюс. Если точка расположена ниже или влево, то расстояние считается отрицательным и отметка ставится со знаком минус. Для полного определения положения точки в проекциях необходимо наличие масштаба и единиц измерения (м, см, мм и т.д.)

В геометрии недр прямая как геометрический элемент обозначает буровую скважину, ось горной выработки, направление простирания или падения. В связи с этим прямая может быть задана:

1. Координатами двух точек:

2. Прямая может быть задана координатами одной точки, дирекционным углом направления (обычно задается в сторону падения) и углом наклона

Существует 3 способа градуирования прямых:

1. С помощью палетки с параллельными линиями;

2. С помощью профиля;

3. Аналитический.

2. Основные виды проекций, применяемые при решении задач в горном деле

Общие сведения о центральном проектировании

С центральным проектированием приходится иметь дело при решении вопросов, связанных с фотографией, фотограмметрией, картографией, кристаллографией. Суть его заключается в следующем.

Для получения изображения предмета М (например, куба) (рис.1.1) на плоскости Р в центральной проекции необходимо выбрать точку О вне плоскости, соединив ее с характерными точками предмета 1,2,……,8 прямыми линиями и найти точки пересечения 1¢,2¢,…….,8¢ этих линий с плоскостью Р . Соединив найденные точки соответствующим образом друг с другом, получают на плоскости Р центральную проекцию данного предмета в виде плоской фигуры m.

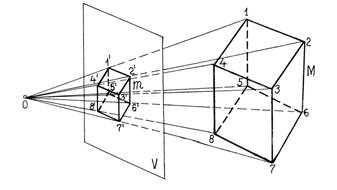
Рисунок 1.1

В этом случае точку О называют полюсом, или центром проекций; предмет М – проектируемым предметом; точки 1,2,…..8 – проектируемыми точками, а их проекции 1¢,2, ¢ …..8¢ – центральными (перспективными) проекциями; прямые линии 0-1,0-2, …, 0-8 – проектирующими линиями или лучами.

Перспективные изображения имеют очень большую наглядность, но малую удобоизмеряемость. В зависимости от формы поверхности, на которой получают изображение, перспективы бывают линейными (изображение строится на плоскости), панорамными (изображение строится на внутренней поверхности цилиндра), купольными (изображение строится на внутренней поверхности шара), диорамными (сочетание линейной перспективы заднего фона предмета с его натуральной величиной на переднем фоне ) и др.

Сущность параллельного проектирования

Метод параллельного проектирования является частным случаем центрального, когда полюс находится на бесконечном удалении от плоскости проектирования. В этом случае проектирующие пучки являются параллельными линиями.

Как видно из рисунка 1.2, если принять РР¢ за направление параллельного проектирования, тогда точки 1¢,2¢,3¢,4¢ будут параллельными проекциями точек 1,2,3,4 – вершин проектируемой пирамиды.

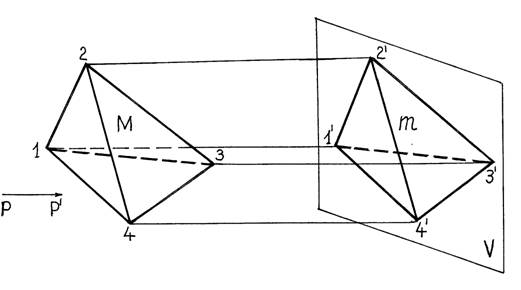
Схема параллельного проектирования предмета

Рисунок 1.2

Фигура m есть параллельная проекция предмета М на плоскость Р.Поэтому параллельное проектирование по сравнению с центральным намного удобно измеримее, но в то же время теряет наглядность.

В геометрии недр наибольшее распространение получили именно проекции, основанные на принципе параллельного проектирования.

При этом методе изображения, как правило, получают на одной или нескольких плоскостях. В зависимости от взаимного положения плоскости проекции и проектирующих лучей различают ортогональное и косоугольное проектирование. В первом случае направление проектирующих лучей перпендикулярно плоскости проектирования, во втором – лучи наклонны к плоскости.

В общем случае параллельное проектирование имеет следующие свойства: отношение отрезков прямой равно отношению их проекций ; проекции двух параллельных прямых параллельны между собой; отношение отрезков двух параллельных прямых равно отношению их проекций.

На принципе параллельного проектирования основаны проекции с числовыми отметками, ортогональные проекции (декартовая система), аксонометрическая и аффинные проекции.

Билет № 2

1. Взаимное положение прямых

Прямые в пространстве могут быть :

а)параллельными;

б)пересекающимися;

в)скрещивающимися.

Прямые в пространстве параллельны если проекции их параллельны, заложения равны и отметки возрастают в одну сторону.

Прямые пересекаются если пересекаются их проекции и точка пересечения для обеих прямых.

Если не соблюдается одно из свойств параллельности прямых, то прямые в пространстве скрещиваются.

Перпендикулярность прямых в пространстве определяется методом совмещения. Если в совмещенном положении прямые перпендикулярны, то они и перпендикулярны и в пространстве.

Решение всех задач на взаимное положение прямых обычно сводится к градуированию их. Таким путем определяется взаимное положение прямых. У параллельных прямых проекции параллельны, интервалы равны и направление возрастания отметок одинаково. Таким образом, если после градуирования прямых окажется, что при параллельных проекциях прямых их интервалы одинаковы, а направление отметок возрастае в одну сторону, то такие прямые будут параллельны.

Пересекающиеся в пространстве прямые изображаются пересекающимися проекциями, а точка пересечения имеет одинаковую отметку.

2. Математическое действие сложение с топографическими поверхностями

При сложении поверхностей могут быть такие случаи.

-Изолинии поверхностей при наложении друг на друга пересекаются, образуя четырёхугольники.

-Изолинии не пересекаются и направлены в одну или противоположные стороны.

-Изолинии при наложении поверхностей имеют весьма сложную конфигурацию.

Накладывая две поверхности друг на друга, определяем, с каким случаем нам придётся иметь дело, затем накладываем на них прозрачный материал, предназначенный для изображений 3-й поверхности.

В первом случае (рис.6.3) отмечаем на чертеже точки пересечения изолиний поверхностей Р и Т , находим суммы отметок в пересечениях и по ним проводим горизонтали суммарной топографической поверхности.

Во втором и третьем случаях построение суммарной топографической поверхности производится с помощью квадратной вспомогательной сетки, выполненной на прозрачном материале, т.е. в вершинах квадратов находят суммарные отметки и по ним строят топографическую поверхность методом интерполирования.

Сложение поверхностей топографического порядка практически применяют при решении многих задач геолого-маркшейдерской службы, например:

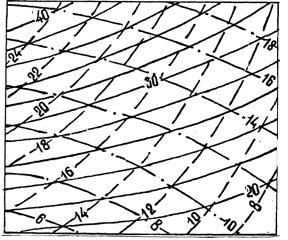
Рисунок 6.3 Графическое сложение двух поверхностей топографического порядка

при определении суммарного объёма нескольких залежей, залегающих друг над другом, по их изомощностям;

в выборе места заложения подъёмного ствола шахты;

при нахождении места своза грузов из нескольких пунктов при минимальных расходах по их перевозке.

Билет № 3

1. Взаимное положение прямой плоскости

Взаимное положение прямой линии и плоскости в пространстве может быть следующим :

а)прямая лежит в плоскости;

б)прямая пересекает плоскость;

в)прямая параллельна плоскости;

г)прямая перпендикулярна плоскости.

Прямая лежит в плоскости, если хотя бы две ее точки совпадают с плоскостью.

Прямая пересекает плоскость, если ее проекция пересекает проекцию любой линии наибольшего ската плоскости.

Прямая параллельна плоскости, если на заданной плоскости можно провести другую прямую и при этом выполнялось бы условие параллельности двух прямых.

Прямая перпендикулярна плоскости, если ее проекция перпендикулярна к горизонталям плоскости, направление падения противоположно направлению падения плоскости, а величина заложения прямой dл равна

dл = h2/dn,

где dn – залажение плоскости ; h – высота сечения.

Скрещивающиеся в пространстве прямые могут изображаться в проекциях с числовыми отметками двояко:

а)проекции скрещивающихся прямых пересекаются, а точка пересечения имеет две отметки;

б)проекции скрещивающихся прямых параллельны, если углы их наклона не одинаковы или же при одинаковых углах прямые наклонены в разные стороны.

2. Математическое действие вычетание с топографическими поверхностями

При вычитании топографических поверхностей в пределах всего плана или отдельных его участков могут быть такие же случаи, как и при сложении поверхностей. Порядок действий при этом такой же. Когда изолинии пересекаются, то отмечают точки пересечения поверхностей и в этих точках вычитанием находят числовые отметки. Соединяя одинаковые отметки изолиниями, проходящими по диагоналям четырёхугольника, образованным изолиниями двух пересекающихся поверхностей, получаем изолинии третьей, являюшейся поверхностью разности.

Во втором и третьем случае, когда изолинии не пересекаются или имеют на плане сложную конфигурацию, вычитание поверхностей лучше производить наложением на них сетки на прозрачном материале и вычитанием отметок одной поверхности из другой в вершинах сетки. Одновременно во всех пересечениях изолиний необходимо делать вычитания и получать целые отметки. Затем обычным способом производится интерполяция и строится поверхность разности.

Вычитание поверхностей производят, например, при построениях:

поверхности кровли залежи на основе дневной поверхности и графика изоглубин;

поверхности почвы залежи на основе поверхности кровли и графика изомошноетей;

поверхности кровли нижележащего пласта на основе поверхности почвы вышележащего пласта и графика изомощности междупластья.

Билет № 4

1. Взаимное положение плоскостей

Плоскости в пространстве могут быть параллельными и пересекающимися.Две плоскости параллельны в том случае, если горизонтали их параллельны и направлены в одну сторону и заложения одинаковы (рис.2.4).

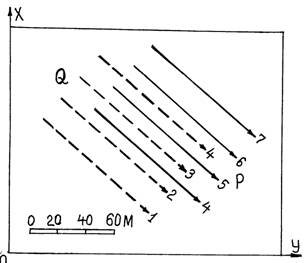
Рисунок 2.4 Условие параллельности плоскостей

Две плоскости пересекаются в следующих случаях:

а)их одноименные горизонтали пересекаются;

б)горизонтали плоскостей параллельны, но имеют противоположные направления;

в)горизонтали плоскостей параллельны, направлены в одну сторону, но имеют различные заложения.

В первом случае плоскости Р и J показаны на рис.2.9,а. Горизонтали их пересекаются в пределах чертежа. Здесь линия пересечения плоскостей прохо-дит через точки пересечения горизонталей с одинаковыми отметками, т.е. точки 1,2,3 .

Дирекционный угол a линии пересечения в сторону ее наклона непосредственно измеряется транспортиром от оси Х на чертеже, а угол наклона d - построением разреза по линии 1-2.

Если же горизонтали двух плоскостей не пересекаются в пределах чертежа (рис.2.9,б), то линию пересечения можно определить при помощи вспомогательных наклонных разрезов (плоскости R и S ). Находим линию пересечения плоскостей R и J (линия 1-2), а также плоскостей R и Р (линия 3-4). Пересечение линий 1-2 и 3-4 дает точку m. Аналогично получаем точку n. Линия mn будет линией пересечения плоскостей Р и J.Отметки точек m и n можно опредеклить интерполированием, а по полученным отметкам – найти уклон линии mn. Дирекционный угол линии пересечения mn определяется на чертеже.

Во втором случае (рис.2.9, в ) нахождение линии пересечения плоскостей производится при помощи вертикального разреза (1-1), перпендикулярного к горизонталям плоскостей. С разреза на план сносим точку (С) пересечения линии 1-2-3 и 4-5-6. Через эту точку проводится линия параллельно горизонталям плоскостей, которая и будет являться линией их пересечения.

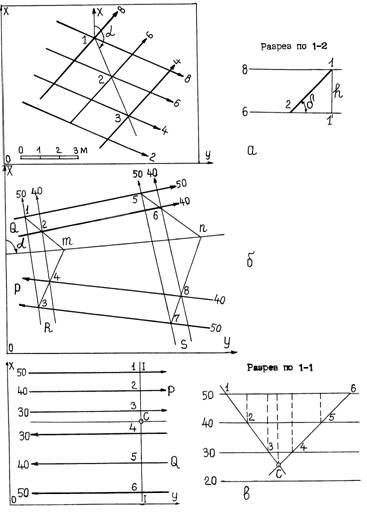
Определение линии пересечения плоскостей

Дирекционный угол a линии пересечения берется с чертежа, а угол наклона d = 00.

2. Математическое действие деление с топографическими поверхностями

Графическое деление поверхностей производят аналогично умножению теми же тремя способами.

Пусть даны две топографические поверхности М=F(X,У) и L=j(X, У).

При разделении этих поверхностей получим третью поверхность

К=f(X,У) , обладающую теми же свойствами, как и исходные поверхности. Здесь необходимо отметить следующее. Поскольку значения функций М и L могут быть произвольными, то может встретиться случай, когда стоящая в делителе функция ( например, L ) пройдет в некоторых точках через ноль. Тогда частное от деления двух функций в этих точках может обратиться в бесконечность и новая функция не будет удовлетворять свойству конечности поверхностей топографического порядка. В этом случае, если функция в делителе отображает конкретные свойства недр и имеет в некоторых участках частное значение, равное нулю, деление поверхностей на этих участках теряет практический смысл, так как изолиния с нулевой отметкой делителя ограничивает участок, в котором представляемый поверхностью делителя показатель залежи отсутствует.

При первом способе для нахождения отметки частного от деления берут изолинию делимого, например, с отметкой 40 (рис.6.7) и находят точку пересечения этой изолинии с изолинией делителя, например 8. Частное от деления дает точку (a) с отметкой 40/8=5. Затем берут следующую изолинию делителя, например, с отметкой 7. Точка ее будет определять частное значение с отметкой 5 в том случае, если делимое в этой точке имеет значение 7х5=35. Тогда линейным интерполированием между изолиниями делимого с отметками 30 и 40 находят изолинию с отметкой 35, которая определит точку (b).

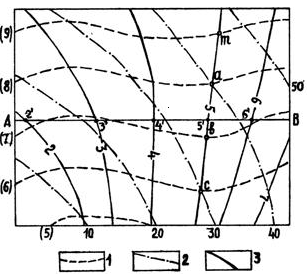
Рисунок 6.7. Графическое деление двух поверхностей

-изолиния поверхности делителя (L);

-изолиния поверхности делимого (М);

-изолиния поверхности частного (К)

Указанным способом находят другие точки с отметкой 5.

Аналогичным образом строят остальные изолинии поверхности частного. Второй способ деления топоповерхностей показан на рис.6.8, где построены кривые логарифмов делимого М и делителя L по профильному сечению АВ (рис.6.7.). По ним найдена кривая логарифма (К) путем вычитания из ординат кривой lg M соответствующих ординат кривой lg L.

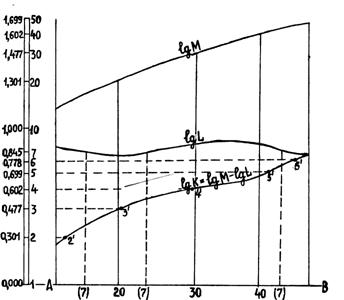
Рисунок 6.8. Логарифмические кривые по линии АВ

По логарифмической шкале определяют ступенчатые отметки, соответствующие значениям lg K, кратные выбранному сечению (например, единице). В нашем примере это точки 2¢, 3¢, 4¢, 5¢, 6¢.

Так же находят ступенчатые отметки частного по другим профильным сечениям. Все полученные отметки выписывают на план и по ним строят изолинии частного.

Деление топографических поверхностей третьим способом может быть произведено с помощью квадратной вспомогательной сетки.

Деление топографических поверхностей используют, например, при построении графика коэффициента вскрыши на открытых разработках, используя график изоглубин и изомощностей залежи.

Билет № 5

1. Определение угла между прямыми

Необходимо определить истинный угол между двумя пересекающимися прямыми b(10) - a(40) и С(0) - a(40), изображенными в проекции с числовыми отметками на рис.2.5.3.

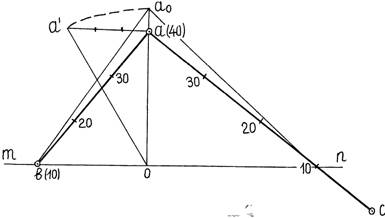
Рисунок 2.13 Определение угла между двумя пересекающимися прямыми

Градуируем прямые bc и сa и находим горизонталь bn c отметкой (10) плоскости, в которой лежит угол bac. Вращаем вокруг этой горизонтали вершину угла – точку a и получаем ее совмещенное положение – точку a0 на продолжении перпендикуляра, опущенного из точки a(40) на горизонталь с отметкой (10).

Соединяем точки b,a0 и n,a0 линиями и получаем истинный угол ba0n между пересекающимися прямыми, который измеряется транспортиром.

2. Математическое действие умножение с топографическими поверхностями

Пусть имеем две поверхности топографического порядка, аналитически выраженные функциями

К=f(X,У) и L=иj(X,У)

Произведение этих поверхностей в общем виде может быть представлено как

М=КL=F(X,У).

Если множители К=f(Х,У) И L=j(Х,У) являются топографическими поверхностями и удовлетворяют свойствам конечности, однозначности, непрерывности и плавности, то произведение этих поверхностей М=F(Х,У) также представляется топографической поверхностью, которая изображается системой непересекающихся линий.

Для умножения двух поверхностей, выраженных в изолиниях, существует три способа.

При первом способе планы, на которых изображены в изолиниях две поверхности, совмещают по координатной сетке. Далее определяют сечение изолиний произведения двух данных поверхностей (рис.6.4), для чего устанавливают минимальное и максимальное значения произведения и число изолиний каждой поверхности. Разность между максимальным и минимальным значениями делится на среднее число изолиний. Частное от деления, округленное до ближайшей цифры, оканчивающейся на 0 или 5, соответствует сечению изолиний функции произведения М.

В нашем примере минимум составляет 1х5=5, а максимум 7х9= =63. Число изолиний первой поверхности равно 7, второй-5. Отсюда нетрудно подсчитать сечение изолиний поверхности произведения, равное 10.

Отмечают точки пересечения изолиний данных поверхностей, отметки произведения которых кратны выбранному сечению (в нашем случае точки a1,b1, С1, d1, имеющие отметки соответственно 10,20,30,40). Если этих точек недостаточно для наведения изолиний поверхности М, находят точки пересечения промежуточных изолиний данных поверхностей. Например, точка Сз , лежащая на изолинии с отметкой 7 поверхности L, будет лежать на изолинии поверхности К с отметкой 30/7=4.3 = 4,3. Полу­ченную отметку поверхности К находят интерполированием между линиями с отметками 4 и 5. Аналогично точка 5, лежащая на изолинии с отметкой 8 поверхности L, будет иметь отметку 30/8=3,7 по поверхности К и находиться между изолиниями с отметкой 3 и 4 и т.д.

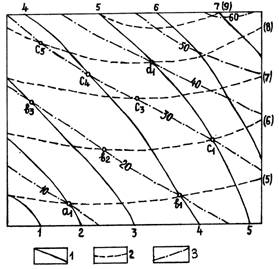
Полученные точки С1, С3 ,..,С5 ... соединяются плавной кривой, которая и будет изолинией поверхности произведения М с отметкой 30.

Подобным же образом находятся точки изолинии произведения с отметкой 20 и т.д.

Второй способ умножения поверхностей называют способом логарифмических кривых. Сущность его состоит в следующем.

На совмешённом плане перемножаемых поверхностей намечают ряд профильных сечений 1-1,П~П,Ш-Ш,1У-1У,У-У (рис. 6.5)

Число сечений зависит от сложности перемножаемых поверхностей и от степени необходимой точности перемножения.

Далее по каждому профильному сечению строят логарифмические кривые для обоих поверхностей, для чего в масштабе исходных поверхностей на ось Х наносят точки пересечения изолиний перемножаемых функций с проекцией профиля, а по оси У откладывают в определённом масштабе логарифмы значений отметок этих точек.

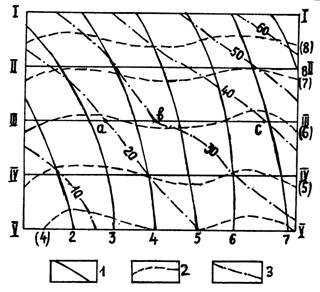
Для каждого профиля получают две кривые логарифма поверхностей К и L . Логарифмические кривые для профиля Ш-Ш построены на рис.6.6. Ординаты кривых графически складывают, получая ряд точек, через которые проводят кривую суммы igМ.

Имея логарифмическую кривую, потенцированием находят ступенчатые отметки, кратные выбранному сечению изолиний поверхности произведения перемножаемых функций (точки a с отметкой 20 м, b с отметкой 30 м и С с отметкой 40 м).

Полученные ступенчатые отметки по всем профильным сечениям переносят на план. Точки с одинаковыми отметками соединяют плавными кривыми, которые представляют собой изолинии поверхности произведения.

Необходимо отметить, что способ построения логарифмических кривых может быть применён для логарифмирования вообще поверхностей топографического порядка.

Логарифмируя изложенным способом графическое изображение функции Р=f(Х,У), получим новую функцию lgР=lgf(X, у)=f(X ,У), которая также выражается топографической поверхностью.

Третий способ вспомогательной сетки рекомендуют в тех случаях, когда на совмещённом плане перемножаемых поверхностей получается недостаточное количество точек пересечения изолиний. Здесь порядок работы следующий.

На совмещённый план данных поверхностей наносят вспомогательную сетку (обычно 2х2 см), вычерчиваемую на кальке.

В вершинах квадратов по изолиниям вначале первой, а затем второй поверхности "на глаз" с точностью до 0,1 сечения определяют числовые отметки. Затем эти отметки перемножают и произведение выписывают на план. Интерполированием находят ступенчатые отметки. Точки с одинаковыми отметками соединяют плавной кривой и получают изолинии поверхности произведения.

Умножение поверхностей топографического порядка применяют при решении многих горногеометрических задач. Например, перемножив график изомошностей залежи на график средних содержаний металла в руде и на среднюю плотность руды, получают топографическую поверхность размещения запасов металла в залежи.

Билет № 6

1. Определение угла между плоскостями

Пусть две пересекающиеся плоскости Р и J изображены горизонталями с отметками (70) и (80) в проекции с числовыми отметками (рис.2.5.4).

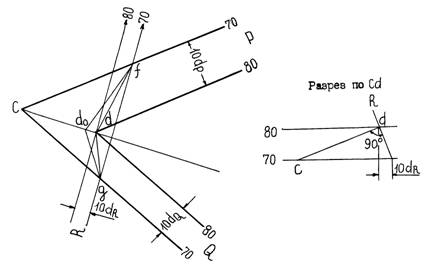
Рисунок 2.14 Определение угла между двумя пересекающимися плоскостями

Если плоскости заданы другими данными, то нужно по ним провести горизонтали.

Линия пересечения плоскостей определится пересечением горизонталей с одинаковыми отметками (линия Сd). Истинный угол между двумя плоскостями находится в сечении (плоскость R), перпендикулярном к линии их пересечения Сd .

Плоскость R должна обладать следующими свойствами:

-её заложение должно быть равно величине 10 dR, определенной с разреза по линии пересечения Сd, как проходящей к ней под углом 900;

-горизонтали плоскости должны быть перпендикулярны линии пересечения Сd;

-направление падения должно быть в сторону, обратную наклону линии пересечения Сd.

Угол ¦dg – это проекция искомого угла на горизонтальную плоскость.Истинный угол можно найти методом совмещения, вращая плоскость R вокруг горизонтали с отметкой (70). В этом случае точка d займет положение d0, и истинный угол между плоскостями Р и J будет ¦d0g. Его замеряют транспортиром.

2. Основные способы определения элементов залегания залежи

Существует 2 способа определения элементов залегания залежи:

1. Непосредственное определение залегания залежи

2. Косвенное определение залегания залежи

Непосредственное определение залегания залежи заключается в том, что с помощью компаса или буссоли определяют простирание и угол падения залежи в местах обнажения полезного ископаемого или по данным геологической разведки по керну. В современном горном производстве используют горный сканер.

Косвенное определение залегания залежи может быть выполнено следующими способами:

1. По результатам кровли залежи изобразить поверхность трех геологических скважин можно в виде топографической поверхности, и по построенным изолиниям можно определить угол простирания и угол падения.

2. По геологическим зарисовкам в вертикальных горных выработках (шурфах).

3. По перекрещивающимся шнурам

Билет № 7

1. Сущность метода совмещения

Для решения многих горногеометрических задач применяют метод совмещения, под которым понимают приведение данной плоскости в положение, параллельное основной плоскости проектирования. Наклонную плоскость J, изображенную семейством горизонталей, можно совместить с горизонтальной или вертикальной плоскостями проекции (рис.2.10). При этом отдельные элементы наклонной плоскости получаются в неискаженном виде, т.е в натуральную величину.

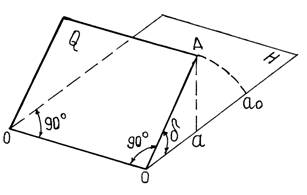
Рисунок 2.5 Схема к методу совмещения

Совмещение наклонной плоскости J с горизонтальной плоскостью проекции Н производится вращением ее вокруг горизонтали ОО1 до их полного совпадения. При этом точка a как горизонтальная проекция точки А на плоскости J займет на плоскости Н положение точки a0 .

Расстояние Оaо равно расстоянию ОА, которое можно вычислить, зная горизонтальную проекцию Оa и вертикальную – Аa по формуле:

ОА = a)2 + (Аa)2

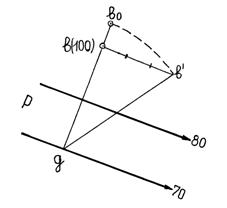
Рисунок 2.6 Определение совмещеного положения точки

Практически гипотенузу ОА не вычисляют, а строят графически по известным горизонтальной и вертикальной ее проекциям (катеты).