11.3. Явление дифракции

Дифракцией называется совокупность явлений, наблюдаемых при распространении волн в среде с резкими неоднородностями и связанных с отклонениями от законов геометрической оптики. Дифракция – характерная особенность распространения волн независимо от их природы. Именно дифракция звуковых волн объясняет возможность слышать голос человека, находящегося за углом дома. Мы ежедневно сталкиваемся с дифракцией радиоволн, слушая радиопередачи и пользуясь сотовым телефоном. Дифракция приводит к огибанию электромагнитными волнами препятствий и проникновению их в область геометрической тени. Из-за дифракции тень от препятствия с прямым краем не бывает идеально резкой: при освещении непрозрачных экранов источником света на границе тени, где, согласно законам геометрической оптики, должен был бы происходить скачкообразный переход от тени к свету, наблюдаются чередующиеся светлые и темные дифракционные полосы (рис. 3.1). Если на пути параллельного светового пучка расположено круглое препятствие, например, диск, шарик, круглое отверстие в непрозрачном экране, то на экране, расположенном на большом расстоянии от препятствия, появляется дифракционная картина в виде чередующихся светлых и темных колец.

Дифракция волн существенно зависит от соотношения между длиной волны и размером объекта, вызывающего дифракцию. 

Наиболее отчетливо дифракция обнаруживается в тех случаях, когда размер огибаемых препятствий соизмерим с длиной волны. Поэтому легко наблюдается дифракция звуковых, сейсмических и радиоволн, для которых длина волны лежит в пределах от нескольких метров до нескольких километров. Значительно труднее наблюдать дифракцию электромагнитных волн оптического диапазона, длины которых лежат в пределах  .Явление дифракции нагляднее всего демонстрируется с помощью волн на поверхности воды. Если размер отверстия или препятствия заметно меньше длины волны, то волна с ним не взаимодействует. Этим обусловлено то, что в шторм волны не проникают в бухту с узким входом. Морские волны длиннее, чем вход в бухту, и не замечают этого входа. Толщина стволов деревьев, стоящих в воде, меньше длины волны, и волны не взаимодействуют с ними (рис. 3.2).

А если размеры препятствия много больше длины волны, то волны за него не проникают, создается область тени: световая тень (рис. 3.3), звуковая тень, ограничения при передаче телевизионного сигнала, невозмущенная поверхность воды за большим валуном (рис. 3.4).

Из-за малости длины волны дифракционные явления в оптике наблюдать сложнее, чем в механике, но их проявления более многообразны и красочны.

Рис. 3.4

Между интерференцией и дифракцией нет существенного физического различия. Оба явления заключаются в перераспределении светового потока в результате суперпозиции волн. Перераспределение интенсивности, возникающее в результате суперпозиции волн, возбуждаемых конечным числом дискретных когерентных источников, принято называтьинтерференцией. Перераспределение интенсивности, возникающее вследствие суперпозиции волн, возбуждаемых когерентными источниками, расположенными непрерывно, называют дифракцией волн.

В строгой постановке дифракционные задачи, ввиду их сложности, допускают аналитические решения лишь в простейших идеализированных случаях. В оптике значительно большее значение имеют приближенные методы решения дифракционных задач, основанные на принципе Гюйгенса в обобщенной формулировке Френеля.

ДИФРАКЦИОННАЯ РЕШЁТКА - оптич. элемент, представляющий собой совокупность большого числа регулярно расположенных штрихов (канавок, щелей, выступов), нанесённых тем или иным способом на плоскую или вогнутую оптич. поверхность. Д. р. используется в спектральных приборах в качестве диспергирующей системы для пространственного разложения эл--магн. излучения в спектр. Фронт световой волны, падающей на Д. р., разбивается её штрихами на отдельные когерентные пучки, к-рые, претерпев дифракцию на штрихах, интерферируют (см. Интерференция света), образуя результирующее пространственное распределение интенсивности света - спектр излучения.

Существуют отражательные и прозрачные Д. р. На первых штрихи нанесены на зеркальную (металлич.) поверхность, и результирующая интерференционная картина образуется в отражённом от решётки свете. На вторых штрихи нанесены на прозрачную (стеклянную) поверхность, и интерференц. картина образуется в проходящем свете.

Если штрихи нанесены на плоскую поверхность, то такие Д. р. наз. плоскими, если на вогнутую - вогнутыми. В современных спектральных приборах используются как плоские, так и вогнутые Д. р., гл. обр. отражательные.

Плоские отражательные Д. р., изготовляемые с помощью спец. делительных машин с алмазным резцом, имеют прямолинейные, строго параллельные друг другу и эквидистантные штрихи одинаковой формы, к-рая определяется профилем режущей грани алмазного резца. Такая Д. р. представляет собой периодич. структуру с пост. расстоянием d между штрихами (рис. 1), к-рое наз. периодом Д. р. Различают амплитудные и фазовые Д. р. У первых периодически изменяется коэфф. отражения или пропускания, что вызывает изменение амплитуды падающей световой волны (такова решётка из щелей в непрозрачном экране). У фазовых Д. р. штрихам придаётся спец. форма, к-рая периодически изменяет фазу световой волны.

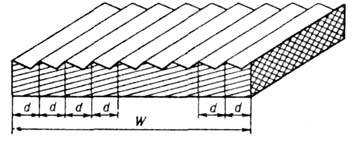
Рис. 1. Схема одномерной периодической структуры плоской дифракционной решётки (сильно увеличено): d - период решётки; W - длина нарезной части решётки.

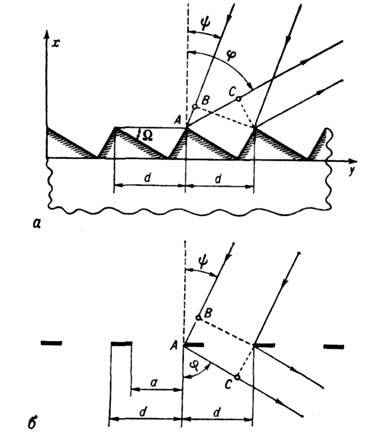
Рис. 2. Схема, иллюстрирующая принцип действия дифракционной решётки: a - фазовой отражательной, б - амплитудной щелевой.

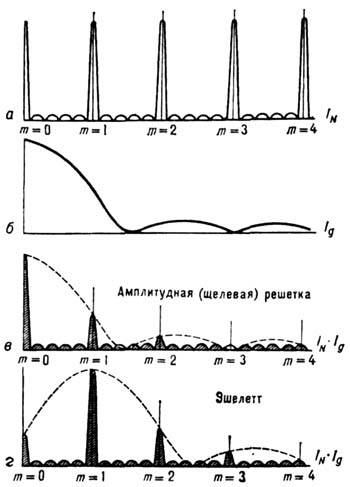
Рис. 3. Интерференционные функции дифракционной решётки.

Если на плоскую Д. р. падает параллельный пучок света, ось к-рого лежит в плоскости, перпендикулярной к штрихам решётки, то, как показывает расчёт, получающееся в результате интерференции когерентных пучков от всех N штрихов решётки пространственное (по углам) распределение интенсивности света (в той же плоскости) может быть представлено в виде произведения двух ф-ций:   . Ф-ция J_gопределяется дифракцией света на отд. штрихе, ф-ция J_N обусловлена интерференцией N когерентных пучков, идущих от штрихов решётки, и связана с периодич. структурой Д. р. Ф-ция J_N для данной длины волны   определяется периодом решётки d, полным числом штрихов решёткиN и углами, образованными падающим (угол ) и дифрагированным (угол ) пучками с нормалью к решётке (рис. 2), но не зависит от формы штрихов. Она имеет вид   , где  ,   - разность хода между когерентными параллельными пучками, идущими под углом   от соседних штрихов Д.р.:  =АВ+АС (см. рис. 2, а - для фазовой отражательной Д. р., 2, б - для амплитудной щелевой решётки). Ф-ция J_N - периодич. ф-ция с резкими интенсивными гл. максимумами и небольшими вторичными максимумами (рис. 3, а). Между соседними гл. максимумами расположено N-2 вторичных максимумов и N-1 минимумов, где интенсивность равна нулю. Положение гл. максимумов определяется из условия   или  , где m=0, 1, 2, ... - целое число. Откуда

т. е. гл. максимумы образуются в направлениях, когда разность хода между соседними когерентными пучками равна целому числу длин волн. Интенсивность всех главных максимумов одинакова и равна   , интенсивность же вторичных максимумов мала и не превышает   от  .

Соотношение   , называемое ур-нием решётки, показывает, что при заданном угле падения  направления на главный максимум   зависят от длины волны  , т. е.  ; следовательно, Д. р. пространственно (по углам) разлагает излучение разл. длин волн. Если дифрагиров. излучение, идущее от решётки, направить в объектив, то в его фокальной плоскости образуется спектр. При этом одновременно образуется неск. спектров при каждом значении числа  , и величина т определяет порядок спектра. При m=0 (нулевой порядок спектра) спектр не образуется, т. к. условие   выполняется для всех длин волн (гл. максимумы для всех длин волн совпадают). 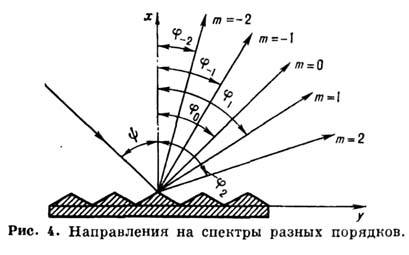Из последнего условия при т=0 также следует, что  , т. е. что направление на максимум нулевого порядка определяется зеркальным отражением от плоскости решётки (рис. 4); падающий и дифрагированный пучки нулевого порядка расположены симметрично относительно нормали к решётке. По обе стороны расположены максимумы и спектры m= 1, m= 2 и T. д. порядков.от направления на макс имум нулевого порядка

Вторая ф-ция J_g, влияющая на результирующее распределение интенсивности в спектре, обусловлена дифракцией света на отд. штрихе; она зависит от величин   , а также и от формы штриха - его профиля. Расчёт, учитывающий Гюйгенса - Френеля принцип, даёт для ф-ции J_g выражение

 ,

где   - амплитуда падающей волны,   - волновое число;  ,  , х и у - координаты точек на профиле штриха. Интегрирование ведётся по профилю штриха. Для частного случая плоской амплитудной Д. р., состоящей из узких щелей в непрозрачном экране (рис. 2, б)или узких отражающих полосок на плоскости, , где  , а - ширина щелей (или отражающих полосок), и представляет собой дифракц. распределение интенсивности при дифракции Фраунгофера на щели шириной а (см.Дифракция света). Вид её приведён на рис. 3 (б). Направление на центр гл. дифракц. максимума ф-ции J_g определяется из условия u=0 или , откуда  , т. е. это направление определяется зеркальным отражением от плоскости Д. р., и, следовательно, направление на центр дифракц. максимума совпадает с направлением на нулевой - ахроматический - порядок спектра. Следовательно, макс. значение произведения обеих ф-ций  , а потому и макс. интенсивность будут в спектре нулевого порядка. Интенсивность же в спектрах остальных порядков (m 0) будет соответственно меньше интенсивности в нулевом порядке (что схематически изображено на рис. 3, в). Это невыгодно при использовании амплитудных Д. р. в спектральных приборах, т. к. большая часть световой анергии, падающей на Д. р., направляется в нулевой порядок спектра, где нет спектрального разложения, интенсивность же спектров других и даже первого порядков мала.

НЬЮТОНА КОЛЬЦА - интерференц. полосы равной толщины в форме колец, расположенных концентрически вокруг точки касания двух сферич. поверхностей либо плоскости и сферы. Впервые описаны в 1675 И. Ньютоном. Интерференция светапроисходит в тонком зазоре (обычно воздушном), разделяющем соприкасающиеся поверхности; этот зазор играет роль тонкой плёнки (см. Оптика тонких слоев ).Н.к. наблюдаются и в проходящем, и - более отчётливо - в отражённом свете. При освещении монохроматич. светом длины волны  Н. к. представляют собой чередующиеся тёмные и светлые полосы (рис. 1). Светлые возникают в местах, где разность фаз между прямым и дважды отражённым лучом (в проходящем свете) или между лучами, отражёнными от обеих соприкасающихся поверхностей (в отражённом свете), равна (п = 1, 2, 3, ...) (т. е.разность хода  равна чётному числу полуволн). Тёмные кольца образуются там, где разность фаз равна  Разность фаз лучей определяется толщиной зазора  с учётом изменения фазы световой волны при отражении (см. Отражение света). Так, при отражении от границы воздух - стекло фаза меняется на  а при отражении от границы стекло - воздух фаза остаётся неизменной. Поэтому в случае двух стеклянных поверхностей (рис. 2), с учётом различий в условиях отражения от ниж. и верх. поверхностей зазора (потеря полуволны), т-етёмное кольцо образуется, если  т. е. при толщине зазора  Радиус r_т т-го кольца определяется из треугольника А-О-С:

Рис. 1. Кольца Ньютона в отражённом свете. 

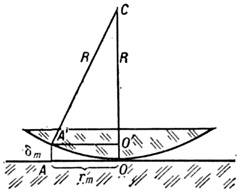
Рис. 2. Схема образования колец Ньютона: О - точка касания сферы радиуса R и плоской поверхности;  - толщина воздушного зазора в области образования кольца радиуса r_m.

Откуда  для тёмного m-го кольца r_т = Это соотношение позволяет с хорошей точностью определять по измерениям r_т. Если  известна, Н. к. можно использовать для измерения радиусов поверхностей линз и контроля правильности формы сферич. и плоских поверхностей. При освещении немоно-хроматич. (напр., белым) светом Н. к. становятся цветными. Наиб. отчётливо Н. к. наблюдаются при малой толщине зазора (т. е. при использовании сферич. поверхностей больших радиусов).