5. Ом және Кирхгоф заңдары

1. Ом заңы

1827 жылы неміс физигі Г. Ом бірнеше тәжірибе өткізіп, электр тогының негізгі заңын шығарды: «Гальваникалық тізбектің ток шамасы, кернеуге тура пропорционал және кедергіге кері пропорционал».

1 I R 2

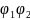
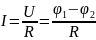- Тізбек бөлігі үшін Ом заңы

Толық тізбек үшін Ом заңы былай анықталады:

, мұндағы - ішкі кедергі.

ЭҚК-сі бар тізбек саласының Ом заңы

Резистор және ЭҚК-сы бар тізбек саласын қарастырайық:

a R b E I c

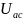
Бұл жағдайда Ом заңы орындалады:

2. Кирхгоф заңдары тармақталған электр тізбектегі ток пен кернеудің байланысын орнатады. Кирхгофтың бірінші заңының негізі – зарядтың сақталу заңы болып табылады: тізбектің кез келген түйініндегі токтардың I_i алгебралық қосындысы нөлге тең:

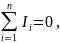(1)

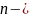түйіндегі токтар саны.

I₁ I₂

I₃

I₅ I₄

Мысалы, жоғарыдағы суреттегі электр тізбегінің түйініне бірінші заң бойынша теңдеуді мына түрде жазуға болады:

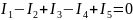
Түйінге бағытталған токтарды оң деп аламыз. Кирхгофтың екінші заңы былайша тұжырымдалады: күрделі электр тізбектегі кез келген тұйықталған контурда, контур кедергісіндегі барлық кернеу шығындарын алгебралық қосындысы, осы контурдағы қорек көзі ЭҚК-нің алгебралық қосындыларына тең, яғни:

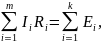(2)

m – тұйықталған контурдағы тармақтар саны, I_i, R_i – і тармағының тогы менкедергісі, k – ЭҚК саны.

I₁ R₁ E₁

I₄ I₂

R₂

R₄

E₂

R₃ I₃ E₃

Белгілердегі ескерту:

1. ЭҚК оң, егер оның бағыты таңдап алынған контурдың аралау бағытымен сәйкес болса;

2. Резистордағы кернеудің шығыны ток бағыты аралау бағытымен сәйкес болса оң болады.

6,Қарапайым және күрделі тұрақты тоқтың сызықты тізбектерін талдау әдістері.

6.Электр тізбектерінің ток әдісі

1)Контурлы ток әдісі

2)Түйін потенциалдар әдісі

3)Беттесу әдісі

4)2 түйін әдісі

5)Эквивалентті генератор әдісі

6)Компенсация принципі

7)Өзара принципі

- 1-әдіс тәуелсіз контурлар саны аз болса Түйін потенциалдар әдісі

- егер бізде түйін саны аз болса Беттесу әдісі

- энергия көздері аз болса 2 түйін әдісі

- тізбекте 2 түйін ғана болса Эквивалентті генератор әдісі

- ток және генератор әдісі тек қана бір тармақтағы токты анықтау үшін

- Компенсация принципі және өзара принципі күрделі тізбектен қарапайым тізбекке ауысу үшін қолданылады

Ендігі кезде Контурлы токтар әдісін қарастыратын болсақ:

Контурлық токтар әдісі біріктіріліп шешілетін теңдеулердің санын K=n-m-n_тк­­+1 шамасына дейін азайтуға мүмкіндік береді және Кирхгофтың екінші заңын қолдануға негізделген .

Әуелі n_тк­­=0 , яғни ток көзі болмаған жағдайда , тізбектің схемасын есептеу үшін қолданылатын әдістің мәніне тоқталайық:

1) K=n-m+1 контурларды және әрқайсысы тиісті контурдың барлық элементтері арқылы жүретін , контурлық токтардың оң бағытын таңдаймыз .

2)Кирхгофтың екінші заңы бойынша , К тәуелсіз контурлар үшін теідеулер құрамыз . Ол теңдеулерді біріктіріп шешкенде контурлардағы барлық контурлық токтар анықталады ;

3)әрбір тармақтың тогын Кирхгофтың бірінші заңы бойынша , тармақтарға тиісті контурлық токтарды алгебралық қосындылау арқылы анықтаймыз .

М ысал ретінде жоғарыдағы суретті келтірейік . Онда n=6 тармақ, m=4 түйін және K=n-m+1=6-4+1=3 контур бар

суретте көрсетілгендей 1-3 тәуелсіз контурларды және олардағы I₁₁, I₂₂ , I₃₃ токтардың оң бағытын анықтаймыз .Тармақтағы токтан ерекше олардың әрқайсысындағы токты контурдың нөмірі арқылы екі іиндекспен белгілейміз . Кирхгофтың екінші заңы бойынша теңдеу құрамыз:

1 -контур

(R₁+R₄+R₆)I₁₁- R₆I₂₂ +R₄I₃₃= E₁-E₄

2-контур)

-R₆I₁₁+(R₂+R₅+R₆)I₂₂ +R₅I₃₃= E₂ (1)

3-контур

R₄I₁₁ +R₅I₂₂+(R₃+R₄+R₅)I₃₃ = E₃-E₄

(1) теңдеулер жүйесінен ауыстыру әдісі немесе ЭЕМ-да сандық әдісті пайдалану арқылы I₁₁, I₂₂ , I₃₃ токтарын анықтайды . Тармақтағы токтарды (суреттегі)Кирхгофтың бірінші заңы бойынша табамыз :

I₁=I₁₁ , I₂=I₂₂, I₃=I₃₃, I₄=-I₁₁-I₃₃, I₅=I₂₂+I₃₃,

I₆=I₁₁-I₂₂