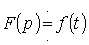20.Өтпелі процестерді есептейтін операторлық әдіс.

Бұл әдіс негізі сонда түпнұсқа болып табылатын t уақыт бойынша ,   функциясы    функциясына сәйкес  жазылады. Бұл өрнек бейне функция деп аталады.Сонда түпнұсқа туындысы мен интегралы бейне функциясының түріне айналады.

Бейнефункция    бойынша    берілген функциясына Лапласс тікелей өрнектеуі арқылы айналады:

.

(1)

Қысқарта жазған кезде түпнұсқаменбейнеарасындабайланысбылайбелгіленеді:

және

.

 Кейбір функциялардың Лапласс түрлендіруінен кейінгі бейнесі

Оригинал

А

Туынды мен интеграл:

Математика курсынан    , болса 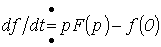   , болатынын білеміз мұндағы    -  функциясының бастапқы мәні.

Сонымен индуктивті элементтегі кернеу:

Немесе нөлдік шарттары

 .

Осыдан

 .

Интеграл үшін дәл солай:

болса    тең

Нөлдік емес шарттар үшін канденсатор кернеуін былай жазамыз:

 .

Сонда

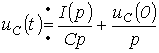
Нөлдік шарттарда:

 ,

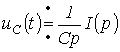Конденсатордың операторлық кедергісі:

 .

21) Өтпелі процестерді есептейтін жиілік әдіс.

Электр тізбегінің алдыңғы режимнен басқа режимге өтуін өтпелі процесс деп атаймыз. Бұл коммутация заңы бойынша орындалады. Коммутация электр тізбегі параметрлерінің идеал электрон кілті көмегімен өзгерісі түсіндіріледі, яғни бір моменттегі өзгерісі. Өтпелі процесті жиіліктік әдіспен есептеу. Жиілікті әдіс Фурье түрлендіруіне негізделген және бұл түрлендірулер Лаплас түрлендірулерінің дербес жағдайы болып табылады. Уақыт функциясын f(t) жиілік функциясына өзгерту Фурьенің тікелей өзгеруі деп аталады, осы түрлендіру функцияның жиілік спектрін береді, ал жиілік спектрдің уақыт функциясына көшуі Фурьенің кері өзгертуі деп аталады .

Фурьенің тікелей өзгертуі

Фурьенің кері өзгертілуі f(t)=

Лаплас пен Фурье өзгертулерін салыстырғанда, олардың ұқсастығы байқалады. Лаплас өзгертуінде р-ны 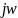ауыстырып, Фурье өзгертілуінің жеке жағдайы болады.

Жиілік спектрі үшін Ом және Кирхгоф заңдары. R,L,C тармақталмаған тізбектегі өтпелі үдерісін, ЭҚК e(t) әсер етуін қарастырып және операторлы мен жиілік әдістер сәйкестігін есепке алып, жиілік спектрін Ом және Кирхгоф заңдарымен жазуға болады. Бастапқы нөл емес жағдайдағы Ом заңы:

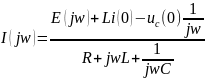
Нөл емес жағдайындағы Ом заңы

Кирхгофтың І заңы:

Кирхгофтың ІI заңы:

Жиілік әдіспен есептеу тәртібі:

1. Кешенді параметрлері бар эквивалентті сұлба құрылады.

2. Кез келген белгілі әдіспен , тоқ пен кернеу жиілік спектрлері анықталады.

3. Ажырату формуласының көмегімен р-ны ауыстырып, түпнұсқаны табамыз, болса, түпнұсқа:

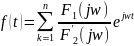
22) Дюамель интегралы. Импульстік сипаттамалар.

Дюамель интегралы – бастапқы шарты нөлге тең, біртексіз импульсті (тұрақты, синусоидалды емес) электр энергиясы әсер ететін пассивті сызықты электр тізбектеріндегі өтпелі процестерді есептейді. Осындай тізбекке біртексіз импульсті Ү(t) әсер етсін. Сонда тоқ пен немесе кернеу:

Мұндағы

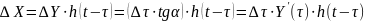
Немесе – Дюамель интегралы

Дюамель интегралының қолданылуы:

1. Тұрақты бірлік ЭҚК қосып, классикалық немесе операторлық әдіспен қажетті өтпелі функцияны ток g(t) және кернеу k(t) бойынша анықтау.

2. g(t-τ) немесе k(t-τ) өтпелі функцияларын t айнымалысын t-τ айнымалысына ауыстыру арқылы табу.

3. ЭҚК функциясынан туынды алып, алынған нәтижелер бойынша t орнына τ айнымалысын қойып, нәтижесінде е'(τ) функциясы алынады.

4. е'(τ), k(t-τ) немесе g(t-τ) функцияларын Дюамель интегралына қойылады, айнымалы τ бойынша интеграл алынып, шекке t айнымалысы қойылады.

Импульстік сипаттамалар. Өтпелі h(t) және импульстік k(t) сипаттамалар сызықты пассивті электр тізбегі үшін, бастапқы шарттары нөлге тең және импульсті әсер етулер кезінде қолданылады. Өтпелі h(t) және импульстік k(t) сипаттамаларды алу үшін 2 арнайы функциялар қолданылады:

1. Бірлік функция

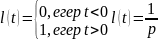
2. Бірлік импульс

Мұнда

Өтпелі h(t) сипаттама – энергия көзінің, тізбектің бастапқы шарты нөлге тең болғандағы, кернеу немесе ток түріндегі бірлік функцияға әсер етуі. Өтпелі h(t) сипаттама t уақытқа, R, L, C параметрлеріне тәуелді. . Өтпелі h(t) сипаттамалар ЭҚК немесе тоқ көзін қосқанда операторлық әдіспен шығарылады.

Импульстік k(t) сипаттамалар – энергия көзінің, тізбектің бастапқы шарты нөлге тең болғандағы, кернеу немесе ток түріндегі бірлік импульске әсер етуі.

Импульсті сипаттама