17.Синусоидалды емес кернеу мен токтын эффективтілік және орташа мәндері.

Синусоидалды емес ток пен кернеудің эффективті мәні дегеніміз сол шамалардың қандай да бір периодтағы орта квадраттық мәні.Сонымен синусоидалды токтың эффективті мәні:

	√	1 Т	T
I =			∫	i2 (t)dt,
			0

Мұнда,

i(t) = I₀ + I_1m sin(ωt + ψ₁) + I_2m sin(2ωt + ψ₂)+ ... +I_km sin(kωt + ψ_k).

Оны интегралдап, мынаны аламыз:

I = √I₀² + I₁² + I₂² + ... + I_k²,

 I₁, I₂, I_k - 1, 2,k-ретті гармоник эффективті мәні.Содан:

I₁ = I_1m/√2; I₂ = I_2m/√2; I_k = I_km/√2.

Дәл солай синусоидалды емес кернеудің эффективті мәні:

и = √U₀² + U₁² + U₂² + ... U_k².

Енді синусоидалды емес ток пен кернеудің орташа мәнін қарастырамыз.

Алдымен синусоидалды емес токтың орташа мәні :

	1 T	T
Icp =		∫	i(t)dt = I0.
		0

Кернеудің мәні дәл осылай жазылады тек I-U, i(t)-u(t) деп ауыстырып жазасыз.

 

18.Электр тізбектеріндегі өтпелі процестер. Өтпелі процестердің пайда болуы және коммутация заңдары.

Өтпелі процесстер дегеніміз - тізбектердегі қандай да бір өзгерістердің әсерінен , режимдердің өзгеруіне әкеп соғар өзгерістердің әсерінен болатын процесстерді айтамыз. Мысалы : коммутациялық құрылғылар , кілт, қосқыштар, қайтақосқыштар, ток көзінен ажырау, қысқа тұйықталу секілді жағдайлар өтпелі процесстерді тудырады.

Өтпелі процесстердің орын алуының физикалық мағынасы тізбекте индуктивті катушкалар мен сыйымдылық конденсаторлардың болуы. Себебі магнит және электр энергиялары коммутация(қосқыштың тұйықталу немесе ажырау процессі) кезінде күрт өзгереді.Өтпелі процесс дифференцалдық өрнекпен сипатталады.

Өтпелі процесстер негізінен өте аз уақытқа созылады. Секундтың милиардтық бөлігі мен секундқа дейін.

Коммутацияның 1-ші заңы: Индуктивный элемент L арқылы өткенге дейінгіt = 0₊ , коммутация кезіндегі , коммутациядан кейінгіt = 0_  ток мәндері өзара тең. Себебі катушкадағы ток лезде өзгере алмайды.

Сонымен , бұл заң магнит өрісінің өзгерісін сипаттайды

W_L = Li² /2

Коммутацияның екінші заңы:  С конденсаторындағы кернеудің коммутацияға дейінгі t = 0₊ , коммутация кезіндегі , коммутациядан кейінгі t = 0_  мәндері тең.Себебі конденсатордағы кернеу күрт өзгеруі мүмкін емес. 

Ал екінші заңы конденсатор кернеуінің біркелкі өзгеруін сипаттайды: 

W_c = Си ²/2

19.Өтпелі процестерді есептейтін классикалық әдіс.

Өтпелі процесстерді классикалық әдіс арқылы есептеу дегеніміз – тізбектегі ток пен кернеудің лездік мәні үшін алгебралық, дифференциалдық теңдеулерін Кирхгов заңдарын пайдалана отырып жазамыз

Бізге қажетті әсерді анықтау үшін өзге айнымалы шамаларды ескермей тұрақты коэффицентті  n-шіретті сызықты теңдеуге айналдырамыз.

Сонымен:

 ,

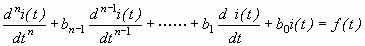 i(t) – қисықтық айнымалы, f(t) –теңдеудің оң бөлігі, қоздырушы күштермен сәйкес. Математика курсынан білетініміз сызықты дифференциал теңдеуді шешкенде ол екі құраушыдан тұрады:

i(t) = i_бейбіт(t) + i_мәжбүр(t) .

f(t) = 0 деп алганда

k ны p^k деп алсақ 

pⁿ + b_n-1p^n-1 + ........... +b₁p + b₀ = 0

Сонымен жалпы шешім:

 A_k –тұрақтыинтегралдау