15.Кешігу буын(өтпелі сипаттамасы)

Мұндай буында кiрiстiк сигнал буын арқылы уақытта өтiп оның шығысына өзгермеген түрiнде келедi. Сондықтан уақытын буынның кешiгу уақыты деп атайды. Бұл буынның теңдеуi мұндағы — таза кешiгу уақыты.

Мұндай буында шығыстық сигнал уақытқа ығыса кiрiстiк сигналын қайталайды.Кiрiстiк сигналы секiрiс түрiнде өзгергенде, шығыстық сигналы 6.15, б-суреттегi өтпелi сипаттамаға сәйкес

өзгеретiн болады. А нүктеде осы сипаттамаға жанама жүргiзiп, бiрiншi жақындасуда объектiнi тiзбектей жалғанған екi буын — таза кешiгуi бар буын және бiрiншi реттi апериодтық буын түрінде қарастыруға болады (6.15, в-сурет).

Кiрiстiк шамаға транспортерге берiлетiн шикiзатты, ал шығысқа оның транспортерден түсiрудi алсақ, онда ағынды тасымалдау кұрылғысын кешiгу буынының шынайы мысалы ретiнде қарастыруға болады. Транспортерден өнімдi тиеу және түсiру уақыт бойынша шамаға ажыратылады. Бұл жағдайда -ды көліктік кешiгу деп атайды.Буынныңөтпелiфункциясы (6.69).Буын теңдеуiнiң операторлық түрi мен берiлiс функциясын кешiгу теоремасын пайдалана отырып, не жиiлiк беріліс функциясы арқылы алуға болады.Буын кiрiсiне гармоникалық әсердi бергенде, онда шығысында фаза бойынша 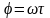бұрышқа ығысатын дәл сондай гармоникалық тербелiс пайда болады.

24.Бірінші ретті апериодтық буын(жиілік сипаттамасы)

Бұл буын бірінші ретті дифференциал теңдеумен өрнектеледі: немесе операторлық түрде былай болады: Статика теңдеуі мына түрде жазылады: , яғни буын позициялы. мүшесінің алдындағы коэффициентті бірге тең етіп алады. Буынның беріліс функциясы

Өтпелі режимде буынның шығыстық шамасы кірістік шаманың өзгерісін лезде қайталамай, шамасымен анықталатын қайсыбір шекті жылдамдықпен біртіндеп өзгереді. Сол себепті бұндай буындарды инерциялы деп атайды.Автоматика элементтерінің ішінде бірінші дәрежелі апериодтық буындар көп тарағаняғни орамдағы процесс бірінші дәрежелі дифференциал теңдеумен өрнектеледі. Мұндай буындар энергия ағынына кедергі тудыратын (актив кедергі) элементтері бар энергиямен қорлануға қабілетті (индуктивтік, сыйымдылық) элементтерді қосу нәтижесінде алынады.

беріліс функциясындағы - ны -мен ауыстырып, жиіліктік беріліс функциясын аламыз: -ның нақты және жорамал бөліктерін , .сонымен қатар модулі мен аргументін алуға болады. Оларды тапқаннан кейін жиілікті 0-ден -ке дейін мен -ның берілген мәнінде өзгерте отырып, амплитудалық-фазалық сипаттаманы салады. АФС төртінші квадратта орналасқан жартылай шеңбер түрінде болады, әрі осы жарты шеңбердің диаметрі буынның беріліс коэффициентіне тең

Жиілік 0-ден -ке дейін артқан сайын буынның шығысындағы тербеліс амплитудасы кемиді, ал осы тербелістің фазасы кірістегі тербеліске қатысты -ге ұмтылады.Модульді логарифмдеу арқылы логарифмдік амплитудалық жиілік сипаттамасын алады: (6.23).Төменгі жиілік аймағында . , яғни апериодтық буынның ЛАС төменгі жиілік аймағында жиілік осіне параллель деңгейінде өтетін түзу болады.