139 из 140

Цифровые схемы

Вопреки навязчивой рыночной рекламе мы живем в аналоговом, а не в цифровом мире. Напряжения, токи и другие физические величины в реальных схемах принимают сколь угодно много значений в зависимости от свойств реальных устройств, состоящих их этих схем. Поскольку реальные величи­ны являются непрерывными, мы можем использовать физическую величину, на­пример, напряжение сигнала в схеме, для представления действительного числа (например, 3.14159265358979 вольт представляют математическую постоянную п с точностью 15 десятичных знаков).

К сожалению, в реальных схемах трудно обеспечить стабильность и точность представления физических величин. На параметры схем влияют многие обстоя­тельства, в том числе технологические допуски, температура, напряжение источ­ника питания, космические лучи и шум, создаваемый другими схемами. Если бы мы использовали аналоговое напряжение для представления к, то обнаружили бы, что величинам, являющаяся абсолютной математической константой, указы­вается с погрешностью в пределах 10% или больше.

Кроме того, многие математические и логические операции трудно или невоз­можно выполнить, используя аналоговые величины. При определенном умении можно создать аналоговую схему, выходное напряжение которой представляет собой квадратный корень входного напряжения. Однако никто никогда не создавал аналоговых схем со 100 входами и 100 выходами, у которых выходные напряжения представляли бы собой набор входных напряжений, упорядоченных по величине.

Цель этой главы - дать твердые практические знания электрических свойств цифровых схем, достаточные для понимания и построения реальных схем и сис­тем. В последующих главах мы увидим, что с помощью современных программ­ных средств можно «создавать» схемы абстрактно, используя для этого языки описания схем, и с помощью моделирующих программ проверять их работоспо­собность. Однако для того, чтобы создавать реальные, высокотехнологичные схе­мы на уровне плат или на уровне ИС, вам все же необходимо понять большую часть материала этой главы. Если вы хотите начать с разработки и моделирования абстрактных схем, то можно прочитать только первый параграф этой главы, а к остальной части вернуться позже.

1. Логические сигналы и вентили

Цифровая логика (digital logic) скрывает подводные камни аналогового мира, отображая бесконечный набор реальных значений физической величины в два подмножества, соответствующих только двум возможным числам или логичес­ким значениям (logic values): 0 и I. В результате цифровые логические схемы мож­но анализировать и разрабатывать функционально, используя алгебру переклю­чений, таблицы и другие абстрактные средства, удобные для описания того, как «ведут себя» нули и единицы в схеме.

Логическую величину 0 или I часто называют двоичной цифрой (binary digit) или битом (bit). Если для решения какой-либо задачи требуется больше двух диск­ретных значений, можно воспользоваться дополнительными битами; набор из п битов представляет 2" различных значений.

Примеры физических явлений, обычно используемых для представления би­тов в современной (и не в очень современной) цифровой технике, приведены в табл. ЗА.У большинства явлений имеется область неопределенности между состо­яниями 0 и I (например: напряжение, равное 1.8 В, слабо светящийся индикатор, лишь частично заряженный конденсатор и т.д.). Эта область неопределенности необходима для того, чтобы состояния 0 и I могли быть однозначно определены и надежно обнаружены. Если границы, отделяющие состояния 0 и I, слишком близ­ки, то шуму легче исказить результаты.

При обсуждении электронных логических схем, выполненных по технологии КМОП и ТТЛ, разработчики часто используют слова «низкий уровень» (LOW) и «высокий уровень» (HIGH) вместо «О» и «I»; им постоянно приходится помнить о том, что они имеют дело с реальными схемами, а не с абстрактными величинами:

• низкий уровень - это сигнал в диапазоне численно малых напряжений, который интерпретируется как логический 0;

• высокий уровень - это сигнал в диапазоне численно больших напряжений, кото­рый интерпретируется как логическая 1.

Заметьте, что присвоение значений 0 и 1 низкому и высокому уровням не­сколько произвольно. Присвоение значения 0 низкому уровню, а значения 1 высо­кому уровню выглядит наиболее естественным и называется положительной ло­гикой (positive logic). Противоположное соответствие, то есть 1 - низкий уровень и 0 - высокий уровень, используется не часто и называется отрицательной логи­кой (negative logic).

Поскольку одному и тому же двоичному значению соответствует широкий диапазон значений физической величины, цифровая логика слабо чувствительна к замене компонентов, вариациям напряжения питания и шуму. Кроме того, для восстановления «ослабленных» значений и преобразования их в «сильные» мож­но использовать буферные усилители (buffer amplifiers), и тогда цифровые сигна­лы можно передать на любое расстояние без потери информации. Например, буферный КМОП-усилитель преобразует любое входное напряжение высокого уровня в выходное напряжение, очень близкое к 5,0 В, и любое входное напряже­ние низкого уровня в выходное напряжение, очень близкое к 0.0 В.

Табл. 3.1. Физические состояния, представляющие биты в компьютерах и системах памяти различного типа

Н е вдаваясь в детали, логическую схему можно представить просто как «чер­ный ящик» с некоторым числом входов и выходов. Например, на рис. 3.1 показана логическая схема с тремя входами и одним выходом. Однако такое представление не дает описания того, как реагирует схема на входные сигналы.

Чтобы получить точное описание электрических процессов в электронной схе­ме, требуется большое количество информации. Однако, поскольку предполагает­ся, что на входы цифровой логической схемы поступают только дискретные сигна­лы 0 и 1, «логическую» операцию, выполняемую схемой, можно описать с помощью таблицы, в которой игнорируются электрические процессы и перечис­лены только дискретные значения 0 и 1.

Рис. 3.1. «Черный ящик», представля­ющий логическую схему с тремя входа­ми и одним выходом

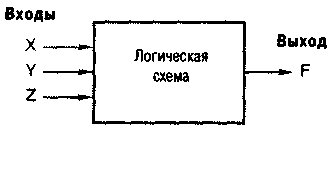
Логическая схема, выходные сигналы которой зависят только от значений ее входных сигналов в данный момент времени, называется комбинационной схемой (combinational circuit). Операция, выполняемая такой схемой, полностью описы­вается таблицей истинности (truth table), в которой перечислены все комбина­ции входных сигналов и соответствующие им значения сигналов на выходе.

Т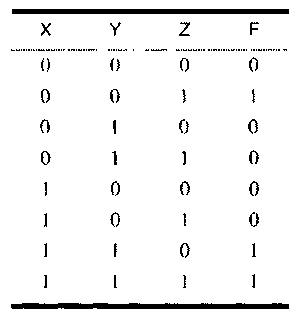 абл. 3.2 представляет собой таблицу истинности для логической схемы с тремя входами X, Y и Z и одним выходом F.

Схема с памятью, выходные сигналы которой зависят от текущих значений вход­ных сигналов и от последовательности значений входных сигналов в прошлом, называется последовательностной схемой (sequential circuit). Поведение такой схемы можно описать таблицей состояний (state table), которая определяет сиг­нал на ее выходе и следующее ее состояние в зависимости от текущего состояния и значений сигналов на входах. Последовательностью схемы будут рассмотрены в главе 7.

Как будет показано в параграфе 4.1, для построения любой комбинационной схемы достаточно только трех основных логических схем, реализующих функции И, ИЛИ и НЕ.

Н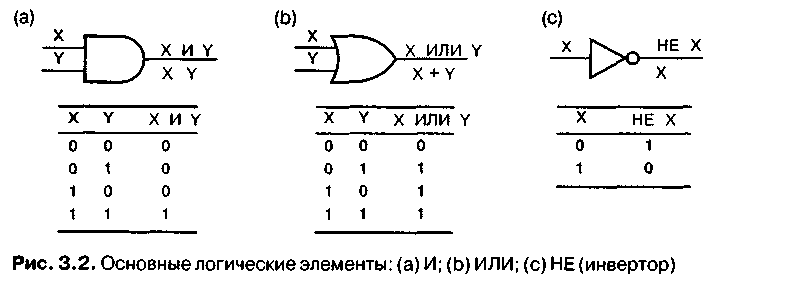 а рис. 3.2 приведены таблицы истинности и условные обозначения логических «вентилей», выполняющих эти функции.

Обозначения и таблицы ис­тинности для схем И и ИЛИ можно расширить на любое число входов. Функции, реализуемые схемами, легко определяются словами:

Схема И (AND gate) вырабатывает 1 на выходе только в том случае, когда на всех ее входах присутствуют 1.

Схема ИЛИ (ORgate) вырабатывает 1 на выходе только в том случае, когда 1 присутствует хотя бы на одном ее входе.

Схема НЕ (NOTgate), обычно называемая инвертором (inverter), вырабатывает на выходе сигнал, противоположный входному сигналу.

Кружок на выходе инвертора является символом инверсии (inversion bubble) и используется в этом и других изображениях логических элементов для обозначе­ния операции «инвертирования».

Обратите внимание, что при определении функций И и ИЛИ нам достаточно было задать только условия на входе, при которых на выходе вырабатывается 1, поскольку в случае, когда выходной сигнал не 1, существует лишь одна возмож­ность: он должен быть равен 0.

Еще две логические функции получены путем объединения функции НЕ с функциями И и ИЛИ в одном вентиле.

Н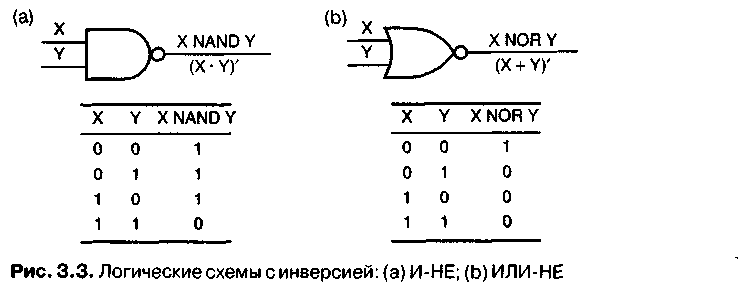 а рис. 3.3 показаны условные обозначения и таблицы истинности для этих схем; функции, реализуемые этими схемами, также легко описать словами:

Схема H-HE(NAND gate) вырабатывает на выходе сигнал, противоположный сигналу на выходе схемы И, то есть 0 только в том случае, когда на всех ее входах присутствуют 1.

Схема ИЛИ-НЕ(NORgate) вырабатывает на выходе сигнал, противоположный сигналу на выходе схемы ИЛИ, то есть 0 только в том случае, когда хотя бы на одном из ее входов присутствует 1.

Так же, как для схем И и ИЛИ, условные обозначения и таблицы истинности для схем И-НЕ и ИЛИ-НЕ можно расширить на любое число входов.

В главе 4 вы узнаете, как переходить от таблицы истинности к логической схеме и обратно, а также познакоми­тесь с системой обозначений алгебры переключений, использованной на рис. 3.2-3.4.

Реальные логические схемы функционируют, кроме того, еще в одном аналоговом измерении – во времени. В качестве примера на рис. 3.5 приведены временные диаграммы, показывающие возможную реакцию схемы, изображенной на рис. 3.4, на меняющуюся во времени комбинацию входных сигналов. Из временных диаграмм видно, что логические сигналы не переходят с одного уровня на другой мгновенно, а имеется запаздывание между изменением сигналов на входе и соответствующим изменением выходного сигнала.

Рис. 3.4 иллюстрирует применения логических схем И, ИЛ И и НЕ для реализации функции F, соответствующей таблице истинности табл.3.2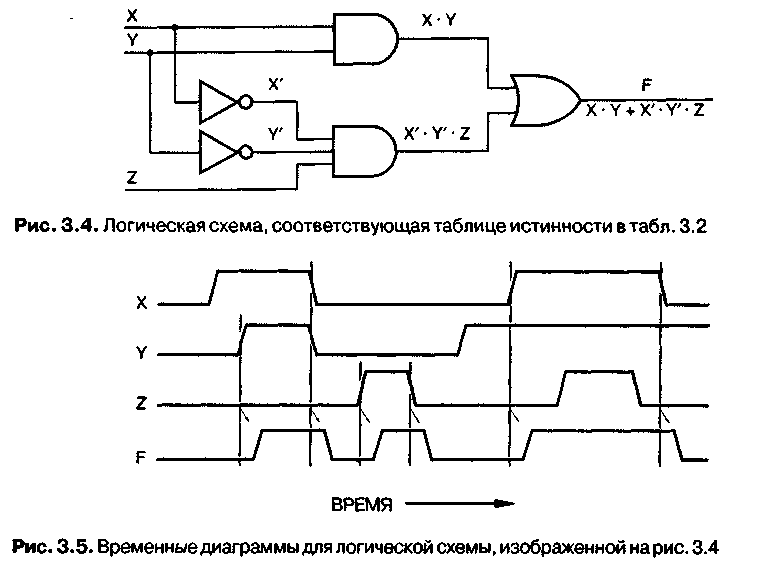

Позже в этой главе вы изучи­те некоторые причины этих задержек и то, как их определять и учитывать в реаль­ных схемах. Вы также узнаете, как в большинстве последовательностных схем этот аналоговый по времени процесс можно вообще игнорировать и считать, что такая схема совершает переход из одного дискретного состояния в другое в моменты времени, определяемые тактовым сигналом.