Факторний аналіз як метод класифікацій в біометрії.
Допустимо, що ви знаходитеся на тій стадії аналізу, коли в цілому знаєте скільки факторів слід виділити. Ви можете захотіти дізнатися значимість факторів, тобто чи можна інтерпретувати їх розумним чином. Для того що би продемонструвати яким чином це може бути зроблено, проводять дії у “зворотному порядку”, тобто починають з деякої осмисленої структури, а потім дивляться, як це відбивається на результатах. Нижче приведена кореляційна матриця що відбиває задоволеність на роботі і дома.
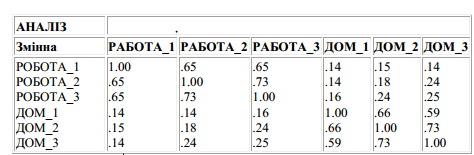
Змінні, що відносяться до задоволеності на роботі тісніше зкорельовані між собою, а змінні, що відносяться до задоволеності удома також тісно зкорельовані між собою. Зкорельованість між обома групами незначна. Тому слід допустити існування двох відносно незалежних факторів. Один відноситься до задоволеності на роботі, а інший - удома. Тепер проведемо аналіз головних компонент і розглянемо рішення з двома факторами. Для цього розглянемо кореляції між змінними і двома факторами, ці кореляції називаються факторними навантаження.
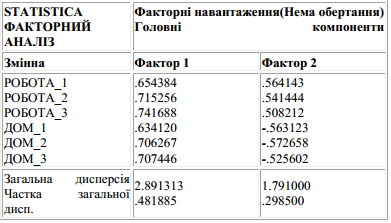Імовірніше,
що перший фактор більш корелює з змінними,
як інший. Це і слід
було чекати, так як фактори виділяються послідовно і містять все менше і менше від загальної дисперсії. Також можна зобразити факторні навантаження у вигляді діаграми розсіювання. На цій діаграмі кожна змінна представлена точкою. Можна повернути вісі в любому напрямі без зміни відносного положення точок, але дійсні координати (тобто факторні навантаження) безперечно зміняться. Якщо повернути діаграму розсіювання для попереднього приклада на 45 град. То досягається більш чіткіше уявлення про навантаження, що визначають змінні, задоволеність на роботі і дома. Методи обертання. Існують різні методи обертання факторів. Метою цих методів є отримання зрозумілої (інтерпретуємої) матриці навантажень. Типовими методами обертання є стратегії варімакс, квартимакс та еквімакс.
Визначення та основні поняття дисперсійного аналізу в біометрії.
Основна концепція дисперсійного аналізу була запропонована в 1920 р. Його суть – аналіз вибіркових дисперсій та розділення дисперсії на частини та компоненти. Основна мета – дослідження значимості різниці між середніми арифметичними вибірок. Розрізняють малофакторний (MANOVA) та багатофакторний (ANOVA) дисперсійні аналізи.
Багатофакторний аналіз.*Чоловіки
Група 1
Група 2
Спост. 1
2
6
Спост. 2
3
7
Спост. 3
1
5
х сер.
2
6
Жінки
Спост. 1
4
8
Спост. 2
5
9
Спост. 3
5
7
х сер.
4
8
Багатофакторний дисперсійний аналіз – аналіз де використовується більше ніж одна змінна. Змінні поділяються на дві групи – зміннні які визначаються в ході експеременту називаються залежними; змінні якими можна керувати в ході експеременту називаються факторними або незалежними. Якщо вирахувати групову дисперсію то дисперсія в першій групі буде дорівнювати 10 ( сума досліджень рівна 10). Звідси внутрішньогрупова дисперсія рівна 20. При врахуванні статі будцть враховуватися 4 групи. Групова дисперсія буде рівна 8.