
- •Суть вибіркового спостереження в біометрії.
- •Вибіркові оцінки середньої та частки.
- •Різновиди вибірок, способи відбору елементів сукупності для обстеження.
- •Визначення мінімально достатнього обсягу вибірки в біометрії.
- •Поняття статистичної перевірки гіпотез.
- •Поняття регресії та види регресії.
- •Двовимірний візуальний аналіз в біометрії
- •Тривимірний візуальний аналіз даних в біометрії.
- •Основна мета та застосування факторного аналізу в біометрії.
- •Факторний аналіз як метод редукції даних в біометрії.
- •Факторний аналіз як метод класифікацій в біометрії.
- •Визначення та основні поняття дисперсійного аналізу в біометрії.
- •Ефекти взаємодій між факторами при багатофакторному дисперсійному аналізі в біометрії.*
- •Суть і складові елементи динамічного ряду.
- •Характеристики інтенсивності динаміки.
- •Середня абсолютна та відносна швидкість розвитку.
- •Характеристика основної тенденції розвитку.
- •Індекси середніх величин.
- •Територіальні індекси
- •Поняття про статистику навколишнього серидовища
- •Побудова системи показників статистики навколишнього серидовища
- •Показники окремих видів природних ресурсів
Визначення мінімально достатнього обсягу вибірки в біометрії.
У процесі проектування вибіркових спостережень визначають мінімально достатній обсяг вибірки, при якому вибіркові оцінки репрезентували б основні властивості генеральної сукупності. Занадто великий обсяг вибірки потребує зайвих витрат, а занадто малий призведе до збільшення похибки репрезентативності. Теорія вибіркового методу дає змогу науково обґрунтувати
достатній обсяг вибірки.
Поняття статистичної перевірки гіпотез.
Статистична гіпотеза — це певне припущення щодо властивостей генеральної сукупності, яке можна перевірити, спираючись на результати вибіркового спостереження. Суть перевірки гіпотез полягає в тому, щоб визначити, узгоджуються чи ні результати вибірки з гіпотезою, випадковими чи
невипадковими є розбіжності між гіпотезою і даними вибірки.
статистична гіпотеза перевіряється в такій послідовності:
а)
формулюють нульову
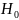 та альтернативну
та альтернативну
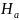 гіпотези;
гіпотези;
б) вибирають статистичну характеристику , за значеннями якої перевіряють правильність нульової гіпотези;
в) визначають рівень істотності і відповідне йому критичне значення ;
г) за результатами вибірки розраховують фактичне (вибіркове) значення
статистичної характеристики , яке порівнюють з критичним , якщо статична характеристика більша критине значення то нульова гіпотеза відхиляється, а якщо менша - невідхиляється.
Види взаємозв’язків між ознаками в біометрії.
Функціональний - кожному значенню фактора х відповідає одне або кілька чітко визначених значень у. Такою, наприклад, є залежність довжини ртутного стовпчика від температури навколишнього середовища. Знаючи х, можна в кожному окремому випадку точно визначити результат у. До функціонального типу належать зв'язки між показниками — адитивні
(а + b + с) або мультиплікативні (а = be, с = a/b), а також залежність середніх величин від структури сукупності.
Стохастичний - кожному значенню ознаки х відповідає певна множина значень ознаки у, які утворюють так званий умовний розподіл. Стохастичний зв'язок, відбиваючи множинність причин і наслідків, виявляється в зміні умовних розподілів.
Кореляційний - різновидом стохастичного і виявляється зміною середніх умовних розподілів.
Поняття регресії та види регресії.
Регресія
- математичне вираження взаємозалежності
між ознаками. Регресі буває лінійною
та нелінійною. Лінійна
регресія описується функцією Y=a+bx
де a
– вільний член регресії
, визначає положення; b
– кутовий коефіцієнт
(b>0 –
пряма залежність, b<0
– зворотня залежність,
b=0 –
залежність відсутня).
Нелінійна регресія
застосовується при нерівномірному
співвідношенні варіацій взаємозв’язаних
ознак. Вона буває степеневою
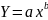 ,
гіперболічною
,
гіперболічною
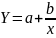 ,
параболічною
,
параболічною
 тощо.
тощо.
Оцінка щільності та перевірка істотності кореляційного зв язку між ознаками. Коефіціент кореляції.*
Поряд із визначенням характеру зв'язку та ефектів впливу факторів х на результат у важливе значення має оцінка щільності зв'язку, тобто оцінка узгодженості варіації взаємозв'язаних ознак. (Щільність зв’язку – ймовірність з якою одна ознака буде впливати на іншу). Якщо вплив факторної ознаки х на результативну у значний, це виявиться в закономірній зміні значень у зі зміною значень х, тобто фактор х своїм впливом формує варіацію у. За відсутності зв'язку варіація у не залежить від варіації х.Для оцінювання щільності зв'язку статистика використовує низку коефіцієнтів з такими спільними властивостями:
• за відсутності будь-якого зв'язку значення коефіцієнта наближається до нуля; при функціональному зв'язку — до одиниці;
• за наявності кореляційного зв'язку коефіцієнт виражається дробом, який за абсолютною величиною тим більший, чим щільніший зв'язок.
Кореляція – величина яка описує щільність зв’язку. В статистиці, коефіцієнт кореляції Пірсона (позначається "r"), є показником кореляції (лінійної залежності) між двома змінними X та Y, який набуває значень від -1 до +1 включно. Він широко використовується в науці для вимірювання ступеня лінійної залежності між двома змінними.
