35. Гаустық қисықтық

Беттің гаустік қисықтығы деп

өрнегін айтады. Бұл инварианттық шама. Шынында да, егер

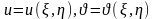(1)формулалары арқылы жаңа координаттарын енгізсек (әрине мұнда (1) түрлендіру мен оның кері түрлендіруін үзіліссіз дифференциалданады деп ұйғарамыз), онда жаңа координаттар арқылы бет

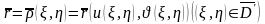теңдеуі арқылы беріледі, мұндағы (1) бейнелеуден шығатын 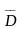тұйық аймағының бейнесі. Сонда

.

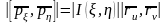Ал 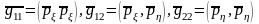деп белгілеулер енгізсек, 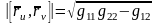болғандықтан 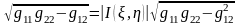(2)

Дәл осылай екінші жартылық тұлға үшін де 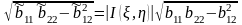(3)

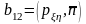
теңдігінің орындалатынын көрсетуге болады, мұндағы , 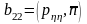. Сондықтан (2), (3) формулалардан (1) түрлен­діруде К(u,v) функциясы өзгермейді. Ал g₁₁g₂₂-g²₁₂ әрқашанда оң болғандықтан беттің эллипстік нүктелерінде гаустік қисық оң, гиперболалық нүктелерде теріс.

36. Бірінші текті беттік интегралда

Шекарасы құрама-жатық контуры болатын құрама-жатық бетінің нүктелерінде анықталған 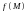функциясы берілсін. Оны құрама-жатық қисық­тармен 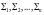бөліктерге бөлшектейік те, бұлардың әрқайсысының ауда­нына сәйкес 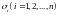арқылы белгілейік. Әрбір бөліктен кез келген 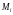нүктесін алып, 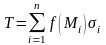қосындысын түзейік. Мұны 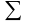бетінің осы бөліктеуге және нүктелерінің осылай таңдап алынуына сәйкес 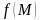функциясының интегралдық қосындысы деп атаймыз.Егер бетінің бөліктері диаметрлерінің ең үлкені нөлге ұмтылғанда интегралдық қосындысы белгілі бір ақырлы шекке ұмтылса, онда бұл шек функциясының беті бойынша бірінші текті беттік интеграл деп аталады және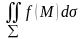 арқылы белгіленеді1-теорема. Айталық, 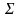жатық беті 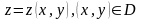теңдеуі арқылы берілсін (мұндағы - тұйық шектеулі аймақ), ал осы бетінде анық­талған шектеулі функция болсын. Онда теңдігі орынды әрі мұның оң жағындағы екі еселі интеграл бар болса, онда сол жағындағы беттік интеграл да бар.

37. Екінші текті беттік интегралдар

Екінші текті беттік интегралды анықтау үшін бізге ең алдымен бет жақтарының ұғымы қажет. Егер бетінде жатқан және оның шекарасымен ортақ нүктесі жоқ кезкелген тұйық контур бойымен жүріп өткенде бет нормалі бағытын өзгертпесе екі жақты бет деп аталады. Егер бойымен жүріп өткен бет нормалы бағытын кері өзгертетін бетте жатқан тұйық контур табылса, онда бет бір жақты бет деп аталады.Жатық регуляр бет бағытталатын бет деп аталады,егер оның бойымен бірлік нормаль векторлар үзіліссіз өрісін таңдау мүмкін болса,егер ондай мүмкіндік жоқ болса, онда бет бағытталмайтын бет деп аталады. Бірлік нормаль векторларының үзіліссіз өрісі таңдап алынған бет бағытталған бет деп аталады.Бағытталған жатық бетін алып, оны бөліктерге бөліп, әрбір бөліктен кез келген бір нүктесін алып,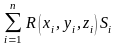 (1)интегралдық қосындысын түземіз, мұнда 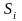арқылы xy жазықтығындағы 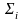проекциясының ауданы белгіленген.Егер бетінің нүктелерінде бет нормалі z өсінің оң бағытымен сүйір бұрыш жасаса, онда шамасын оң деп, ал егер элементінің әрбір нүктесінде бұл бұрыш доғал болса, онда шамасын теріс деп есептейміз. бетін бөлуде кейбір нүктелерінде мұндай бұрыштар сүйір, ал кейбір нүктелерінде доғал болатын да элементтері кездесуі мүмкін. Мұндай жағдайда сондай элементтерді тағы да бұрыш доғалдығына байланысты бөліктеп жіберуге болады. Дәл екінші ретті қисық сызықты интегралдағыдай үзіліссіз R(x,y,z) функциясы мен жазық бет үшін (1) интегралдық қосындылардың бет бөліктеуін шексіз майдалауда шегі бар болса, онда оны

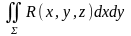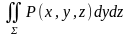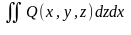(2)түрінде белгілеп, функциясының бетінің таңдап алынған жағы бойынша -текті беттік интеграл деп атаймыз.Осылай интегралдық қосындылар арқылы және интегралдарды да анықтауға болады. Екінші текті беттік интегралдың бірінші текті беттік интегралдан негізгі өзгешелігі екінші текті беттік интегралда аудан элементі бетке нормаль бағытыменбағытталған,компоненттер болатын вектор. 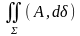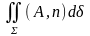Осыған байланысты A=(P,Q,R) вектор-функциясының екінші текті беттік интегралын жиі (3)түрінде жазады, ал ол (4)

жазуына тең мағыналы.