33. Бет бөліктерінің жанама жазықтықтағы аудандары

Егер құрама-жатық L контурымен шектелген жатық беті берілсе, онда оны құрама-жатық қисықтармен 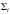бөліктерге бөлеміз де оның әрқайсы­сынан кез келген бір M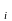 нүктесін алып, сол нүкте арқылы бетіне жанама жазықтық жүргіземіз. Сонан соң 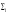бөлігін осы жанама жазықтығына проекция­лап, белгілі бір S_i жазық фигурасын аламыз. бетінің ауданы деп бөліктеу диаметрі нөлге ұмтылғанда бөлшектер проекциялары аудандарының қосындысының шегін айтамыз. Осындай шегі бар бет шаршыланатын бет деп аталады. Ал, жатық бет ауданының формуласы мына теорема арқылы анықталады.теорема. Егер құрама-жатық контурмен шектелген жатық бет 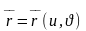теңдеуімен анықталса, онда бұл шаршыланатын бет болады және оның ауданы S= мұнда және 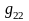арқылы бірінші шаршылық тұлғаның еселеуіштері, ал D арқылы және айнымалыларының өзгеру аймағы белгіленген.Дәлелдеу. бетін бөліктерге бөліп, олардың әрқайсысынан M_i нүктесін алып, сол нүкте арқылы жанама жазықтық жүргіземіз. Сонан соң M_i нүктесін бас нүкте етіп, z осі үшін нормаль бағытын, ал ху жазықтығы үшін жанама жазықтықты алып жергілікті декарт координаталар жүйесін енгіземіз. бетінің кез келген нүктесінің x,y және z координаталарын және айнымалыларының функциясы деп жазуға болады. (Дәлірек, деп жазған дұрыс болар еді, өйткені бұл теңдеулер M_i нүктелеріндегі нормальмен і-ші координата жүйесіне сәйкес жанама жазықтықпен байланысты).Ал, бетінің M_i нүктесіндегі жанама жазықтық проекциясы 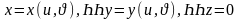теңдеулері арқылы анықталады. Енді жазық фигураның қисықсызықты координаттардағы ауданының өрнегін пайдалансақ бұл проекция ауданын

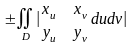
түрінде жазар едік, мұнда Di арқылы (x,y,z) айнымаларға өзгергенде u және 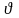өзгеретін аймақ белгіленген.Енді 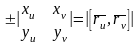болғандықтан, (демек, Di) аймағы жеткілікті кішкене болғанда

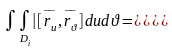мұнда 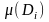арқылы D_i аймағының ауданы 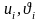арқылы M_i нүктенің коор­динаттары белгіленген және бетін бөліктеуді майдаланған сайын . Сонымен, бет бөліктерінің сәйкес жанама жазықтықтағы проекциялары аудандарының қосындысы 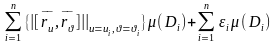.(1)

Бөлшектеуді шексіз майдалауда бұл өрнектің шегі бет ауданына ұмты­лады, ал ол (2)интегралына тең.Егер 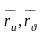векторларының арасындағы бұрышты арқылы белгілесек, онда

.Сонда(1) интегралды былай S= жазуға болады. Теорема дәлелденді.

34. Бет бойындағы сызықтар қисықтығы. II ші шаршылық тұлға.

Өзімен өзінің қиылысы жоқ теңдеуі арқылы берілген екі рет жатық бетін қарастырайық. Егер x=x( ), y=y( ), z=z( )

функцияларының екінші ретті дербес туындылары G аймағында үзіліссіз болса, онда бетті екі рет жатық деп атаймыз.

Егер 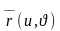вектор функциясына

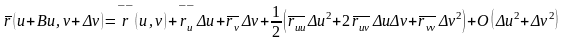
Тейлор формуласын қолданып, мұның екі жағын да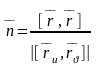

бірлік нормаль векторына скаляр көбейтіп,

теңдіктерін ескерсек,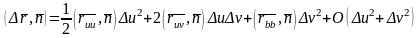

теңдігін аламыз, мұндағы Бұл формуланы

белгілеулерін енгізіп,

ыңғайлы түрде жазайық, мұнда 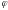арқылы 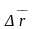және 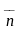векторларының арсын­дағы бұрыш белгіленген. Өрнек 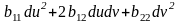беттің екінші шаршылық тұлғасы деп аталады. Беттің екінші шаршылық тұлғасы бет нүктелерін мынадай кластарға бөледі 1. Eгер екінші шаршылық тұлға таңбасы анықталған (яғни 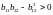болатын) бет нүктелері эллипстік деп аталады. Бұл жағдайда (1)

тұлғадан ( ) нүктесінің жеткілікті кішкене маңайында (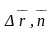 ) скалярлық көбейтінді өз таң­басын сақтайтынын көреміз. Демек, нүктесіне жеткілікті жақын жатқан бет нүктелері нүктесіне жүргізілген жанама жазықтықтың бір жағында жатады. 2. Екінші шаршылық тұлғаның таңбасы айнымалы, яғни 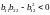болатын бет нүктелері гиперболалық деп аталады. Бұл жағдайда (1) формула бойынша нүктесінің кез келген маңайында осы нүктесіне жүргізіл­ген жанама жазықтықтың екі жағында да жататын бет нүктелері табылады.

3. 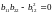болатын бет нүктелері параболалық деп аталады.