
- •4. Тұрақты функциясының тіктөртбұрышта интегралдануы.
- •8. Шектеулі функция Риман бойынша интегралдану критерийі
- •10. Жордан бойынша өлшемді және өлшенбейтін жиындар
- •11. Жордан өлшемінің нөлге тең болу критерийі
- •12.Шектеулі жиын өлшемді болу критерийі
- •13. Үзіліссіз функция графигінің өлшемінің нөлге теңдігі
- •14. Түзуленетін қисық өлшемінің нөлге теңдігі
- •18. Ауданды қисық сызықты координаттар арқылы есептеу.
- •26. Тұйық контур бойынша интег.Нөлге тең болу критериийі.
- •29. Даламбер теңдігінің орындалу критерийі
- •31. Беттің жанама жазықтығы жане нормалі.
- •33. Бет бөліктерінің жанама жазықтықтағы аудандары
- •34. Бет бойындағы сызықтар қисықтығы. II ші шаршылық тұлға.
- •35. Гаустық қисықтық
- •36. Бірінші текті беттік интегралда
- •37. Екінші текті беттік интегралдар
- •38. Екінші текті беттік интег.Екі еселі интег.Келтіру
- •39. Остроградский формуласы.
- •40.Стокс формуласы
29. Даламбер теңдігінің орындалу критерийі
30. Бет,бет бойындағы
қисық.Егер
 жазықтығының D ашық жиынында берілген
жазықтығының D ашық жиынында берілген
 функциясының бірінші ретті дербес
туындылары үзіліссіз болса, онда R3
кеңістігінің осы функция арқылы
сипатталатын
функциясының бірінші ретті дербес
туындылары үзіліссіз болса, онда R3
кеңістігінің осы функция арқылы
сипатталатын
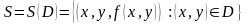 жиыны
жатық
бет
деп аталады.Біз
функциясын да,
жиыны
жатық
бет
деп аталады.Біз
функциясын да,
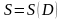 жиынын да бет деп, дәлірек,
беті, S беті деп айта беретін боламыз.Егер
жиынын да бет деп, дәлірек,
беті, S беті деп айта беретін боламыз.Егер
 теңдеуін қарастырсақ, онда біз беттердің
кең класын аламыз. Бет анықтамасын
координаттары
немесе
теңдеулерді қанағаттандыратын
нүктелер жиыны ретінде қарастыру
соншалықты ыңғайлы емес, сондықтан
бетті параметрлік теңдеулер арқылы
берген қолайлы, uv жазықтығының G жиынының
R3
евклид кеңістігіне
теңдеуін қарастырсақ, онда біз беттердің
кең класын аламыз. Бет анықтамасын
координаттары
немесе
теңдеулерді қанағаттандыратын
нүктелер жиыны ретінде қарастыру
соншалықты ыңғайлы емес, сондықтан
бетті параметрлік теңдеулер арқылы
берген қолайлы, uv жазықтығының G жиынының
R3
евклид кеңістігіне
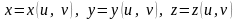 (1)үзіліссіз
(1)үзіліссіз
 бейнелеуі
бет
деп аталады.
бейнелеуі
бет
деп аталады.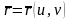 теңдеу арқылы берілген бет теңдеуінің
u,v параметрлерін жаңа t параметрден
тәуелді десек, яғни u=u(t), v=v(t) болса, онда
t-нің әрбір мәніне беттің белгілі бір
нүктесі сәйкес келеді де ол белгілі бір
қисықты анықтайды. Сонымен, қисық бойында
u, v координаталары t параметрінің
функциялары болады:u=u(t), v=v(t) (2)Бұл
теңдеулер бетте берілген қисық тендеулері
деп аталады. Оларды бет теңдеулеріне
қойсақ, бет бойындағы қисықтың
r=r(u(t),v(t))(3)параметрлік теңдеуін аламыз.
теңдеу арқылы берілген бет теңдеуінің
u,v параметрлерін жаңа t параметрден
тәуелді десек, яғни u=u(t), v=v(t) болса, онда
t-нің әрбір мәніне беттің белгілі бір
нүктесі сәйкес келеді де ол белгілі бір
қисықты анықтайды. Сонымен, қисық бойында
u, v координаталары t параметрінің
функциялары болады:u=u(t), v=v(t) (2)Бұл
теңдеулер бетте берілген қисық тендеулері
деп аталады. Оларды бет теңдеулеріне
қойсақ, бет бойындағы қисықтың
r=r(u(t),v(t))(3)параметрлік теңдеуін аламыз.
31. Беттің жанама жазықтығы жане нормалі.
r=r(u(t),v(t)) тендеу
арқылы анықталған қисықтың жанамасын
қарастырайық оның бағыты


Векторыарқылыанықталады,яғниолкоординаттықвекторлардепаталатынберілгеннүктеарқылыөтетінкоординаттықсызықтарғажанама
 векторыныңкөшені.Олардықысқаша
векторыныңкөшені.Олардықысқаша (1)арқылыбелгілейміз.
(1)арқылыбелгілейміз.
Бізрегулярлықжатықбеттердіқарастырамыз.
Егер (1) векторлар G
аймағыныңкезкелгеннүктесіндесызықтықтәуелсізболса,
яғникезкелген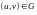 үшін
үшін Матрицасының
рангі 2-ге тең болса, онда бет регулярлық
деп аталады. Мысалы,
Матрицасының
рангі 2-ге тең болса, онда бет регулярлық
деп аталады. Мысалы,

болса, онда
регулярлық беттің әрбір нүктесінде
нормаль бар, өйткені
 векторлары жанама жазықтықта жатады,
ал
векторлары жанама жазықтықта жатады,
ал
 -
оған нормаль вектор.
-
оған нормаль вектор.
Жанама жазықтықтың
теңдеуі(ρ-r,n)=0(2)арқылы анықталады, мұндағы
r – жанаунүктесінің радиусы, ал ρ –
жанамажазықтық нүктесінің радиус-векторы.Егер
бет теңдеуі z=f(x,y) арқылы берілсе,онда
оның векторлық түрін былай
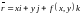 жазуға болады. Енді осындай бетке жанама
жазықтық теңдеуін жазайық. Ол үшін
жазуға болады. Енді осындай бетке жанама
жазықтық теңдеуін жазайық. Ол үшін
 координаттық векторларын және
координаттық векторларын және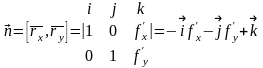 (3)нормаль
векторын табамыз да, (2) жанама жазықтық
теңдеуіндегі -r
орнына i(x-x0)+j(y-y0)+k(z-z0),
ал
(3)нормаль
векторын табамыз да, (2) жанама жазықтық
теңдеуіндегі -r
орнына i(x-x0)+j(y-y0)+k(z-z0),
ал
 нормаль векторының орнына (3) өрнекті
қойып, z=f(x,y) бетін (x0,y0,z0)
нүктесінде жанайтын
z-z0=fx’(x-x0)+fy’(y-y0) (4)жанама
жазықтық теңдеуін аламыз, мұндағы
нормаль векторының орнына (3) өрнекті
қойып, z=f(x,y) бетін (x0,y0,z0)
нүктесінде жанайтын
z-z0=fx’(x-x0)+fy’(y-y0) (4)жанама
жазықтық теңдеуін аламыз, мұндағы
 дербес туындыларының мәндері (x0,y0)
жанау нүктесінде алынады.
дербес туындыларының мәндері (x0,y0)
жанау нүктесінде алынады.
32. Бет бойындағы
ұзындықты, бұрышты есептеуӘрбір
жазықтықта коллинеар емес екі
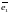 және
және
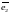 векторлары (оларды, әдетте, репер деп
атайды) координаттар жүйесін анықтайды
және осы жазықтықта кез-келген
векторлары (оларды, әдетте, репер деп
атайды) координаттар жүйесін анықтайды
және осы жазықтықта кез-келген
 векторын былай
векторын былай
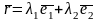 түрінде
өрнектеуге болады. Ал мұның квадраты
түрінде
өрнектеуге болады. Ал мұның квадраты Енді
Енді
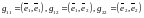 белгілеулерін енгізіп, оны
белгілеулерін енгізіп, оны
 2=
g1112+2
g1212+
g2222(1)түрінде
жазамыз. Сонда
векторының ұзындығы
тікелей (1) формуладан шығады.Егер
2=
g1112+2
g1212+
g2222(1)түрінде
жазамыз. Сонда
векторының ұзындығы
тікелей (1) формуладан шығады.Егер
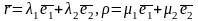
екі векторы берілсе,
онда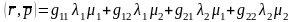 Сонда
cos(
,
Сонда
cos(
,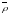 )=
)=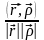 формуласын пайдаланып, r және
векторларының арасындағы бұрышты
олардың координаттары мен
формуласын пайдаланып, r және
векторларының арасындағы бұрышты
олардың координаттары мен
 еселеуіштері арқылы өрнектеуге
болады.Егер қисық
еселеуіштері арқылы өрнектеуге
болады.Егер қисық
 бетінің
бойында берілген болса, онда оның
ұзындығының формуласы да
бетінің
бойында берілген болса, онда оның
ұзындығының формуласы да
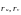 реперлеріне сәйкес g11,
g12,
g22
еселеуіштеріарқылы есептеледі.Шынында
да, бұл қисық бойынан параметр үшін доға
ұзындығын алып, оның теңдеуін
реперлеріне сәйкес g11,
g12,
g22
еселеуіштеріарқылы есептеледі.Шынында
да, бұл қисық бойынан параметр үшін доға
ұзындығын алып, оның теңдеуін
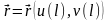 түрінде
жазуға болады. Ал
түрінде
жазуға болады. Ал
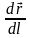 векторының
ұзындығы бірге тең болғандықтан
векторының
ұзындығы бірге тең болғандықтан
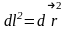 .
.
Енді
бұған
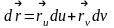 қойсақ,
онда
қойсақ,
онда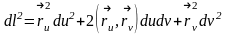 .Егер
.Егер
 белгілеулерін енгізсек,
белгілеулерін енгізсек,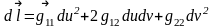 (14)Бұл
өрнек
(14)Бұл
өрнек
 және
және
 өрнектері арқылы оң анықталған шаршылық
тұлға. Мұны
бетінің бірінші шаршылық тұлғасы деп
атайды. Сонымен, беттің бірінші шаршылық
тұлғасы доғаның шексіз аз элементі
ұзындығының өрнектеуін береді. Мұнан
бетте жатқан ақырлы қисық ұзындығын
интегралдау арқылы табамыз, яғни егер
бетте қисық u = u(t), v = v(t), t1
≤ t ≤ t2теңдеулері
арқылы берілсе, онда оның ұзындығы
өрнектері арқылы оң анықталған шаршылық
тұлға. Мұны
бетінің бірінші шаршылық тұлғасы деп
атайды. Сонымен, беттің бірінші шаршылық
тұлғасы доғаның шексіз аз элементі
ұзындығының өрнектеуін береді. Мұнан
бетте жатқан ақырлы қисық ұзындығын
интегралдау арқылы табамыз, яғни егер
бетте қисық u = u(t), v = v(t), t1
≤ t ≤ t2теңдеулері
арқылы берілсе, онда оның ұзындығы
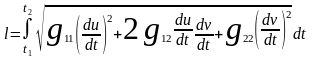 Екі
қиылысатын қисықтар арасындағы бұрыш
деп оларға қиылысу нүктесінде жүргізілген
жанамалар арасындағы бұрышты айтады.
Сонда екі қисық арасындағы бұрыш
Екі
қиылысатын қисықтар арасындағы бұрыш
деп оларға қиылысу нүктесінде жүргізілген
жанамалар арасындағы бұрышты айтады.
Сонда екі қисық арасындағы бұрыш
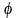
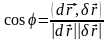 формуласынан
анықталады.
формуласынан
анықталады.
