
- •4. Тұрақты функциясының тіктөртбұрышта интегралдануы.
- •8. Шектеулі функция Риман бойынша интегралдану критерийі
- •10. Жордан бойынша өлшемді және өлшенбейтін жиындар
- •11. Жордан өлшемінің нөлге тең болу критерийі
- •12.Шектеулі жиын өлшемді болу критерийі
- •13. Үзіліссіз функция графигінің өлшемінің нөлге теңдігі
- •14. Түзуленетін қисық өлшемінің нөлге теңдігі
- •18. Ауданды қисық сызықты координаттар арқылы есептеу.
- •26. Тұйық контур бойынша интег.Нөлге тең болу критериийі.
- •29. Даламбер теңдігінің орындалу критерийі
- •31. Беттің жанама жазықтығы жане нормалі.
- •33. Бет бөліктерінің жанама жазықтықтағы аудандары
- •34. Бет бойындағы сызықтар қисықтығы. II ші шаршылық тұлға.
- •35. Гаустық қисықтық
- •36. Бірінші текті беттік интегралда
- •37. Екінші текті беттік интегралдар
- •38. Екінші текті беттік интег.Екі еселі интег.Келтіру
- •39. Остроградский формуласы.
- •40.Стокс формуласы
18. Ауданды қисық сызықты координаттар арқылы есептеу.
D құрама жатық Г
қисығымен қоршалған тұйық аймақ, ал
 осы D аймағында берілген үзіліссіз
немесе өлшемі нөлге тең жиында үзілісті,
бірақ шектеулі функция болсын. Сонымен
бірге
осы D аймағында берілген үзіліссіз
немесе өлшемі нөлге тең жиында үзілісті,
бірақ шектеулі функция болсын. Сонымен
бірге
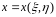 ,
,
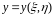
функциялары
белгілі бір G аймағын
аймағына көшіретін шарттарды
қанағаттандыратын бейнелеу болсын.
Мақсатымыз D аймағы арқылы алынған
 интегралын интеграл астындағы өрнекті
жаңа
интегралын интеграл астындағы өрнекті
жаңа
 айнымалыларына түрлендіріп, Gаймағы
бойынша алынған интеграл
түрінде өрнектеу.теорема.
Егер
айнымалыларына түрлендіріп, Gаймағы
бойынша алынған интеграл
түрінде өрнектеу.теорема.
Егер
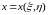 ,
,
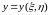 функциялары
Gаймағын
D аймағына көшіретін якобианы нөлден
өзгеше өзара бірмәнді , үзіліссіз және
үзіліссіз дифференциалданатын бейнелеу
болса, онда
функциялары
Gаймағын
D аймағына көшіретін якобианы нөлден
өзгеше өзара бірмәнді , үзіліссіз және
үзіліссіз дифференциалданатын бейнелеу
болса, онда

Дәлелдеуі.
D аймағынан екі пар шексіз жақын жатқан
координаттық сызықтарын алып, бұлардың
біреуіне ξ координатасының
 және
және

мәндерін, ал
екіншісіне
 координатасының
координатасының
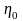 және
және
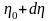 мәндерін сәйкес қоялық.
мәндерін сәйкес қоялық.

Бұл координаттық
сызықтар D аймағынан аздық реті бірден
жоғары дәлдікке дейін параллелограм
болатын
 ауданның шексіз аз элементін қияды.Бұл
параллелограмның қабырғалары
ауданның шексіз аз элементін қияды.Бұл
параллелограмның қабырғалары
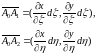 векторлары.
паралелограмның ds
ауданы
векторлары.
паралелограмның ds
ауданы
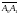 ,
,
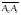 векторларының компоненттерінен түзілген
анықтауыш абсолют шамасына тең, яғни
ds=
векторларының компоненттерінен түзілген
анықтауыш абсолют шамасына тең, яғни
ds=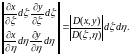 Ал
D аймағының ауданы барлық осындай
элементтерді қосындылаудан шығады,
яғни, шынында да,
Ал
D аймағының ауданы барлық осындай
элементтерді қосындылаудан шығады,
яғни, шынында да,
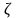 және
айнымалылары өзгеретін G аймағы арқылы
алынған
және
айнымалылары өзгеретін G аймағы арқылы
алынған
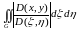 қос интегралы түрінде өрнектеледі
қос интегралы түрінде өрнектеледі
19. Екі еселі интегралда айнымалыларды ауыстыру.
1. Аймақтарды
бейнелеу.
Декарттық координаттары x, y және
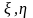 болатын
екі жазықтықты қарастырайық және xy
жазықтығында шекарасы Г тұйық шектеулі
D аймағын, ал ξ,ŋ жазықтығында шекарасы
тұйық шектеулі G
аймағын алайық.
болатын
екі жазықтықты қарастырайық және xy
жазықтығында шекарасы Г тұйық шектеулі
D аймағын, ал ξ,ŋ жазықтығында шекарасы
тұйық шектеулі G
аймағын алайық.


Бүкіл G аймағын (ξ,ŋ) нүктесі басып өткенде оған сәйкес (x, y) нүктесі бүкіл D аймағын басып өтетін G аймағында
 (1)
функциялары анықталған деп ұйғарамыз,
яғни (1) функциялары G
аймағын
аймағына
бейнелеуді
анықтайды.Сонымен бірге бұл бейнелеу
мына шарттарды қанағаттандырады деп
ұйғарамыз: 1) Бейнелеу өзара бір мәнді,
яғни G аймағының әр түрлі нүктелеріне
міндетті
түрде D
аймағының
әр түрлі нүктелері сәйкес келеді. Басқаша
айтқанда,
теңдеулердің
бүкіл D аймағында
бірмәнді анықталған ξ
және ŋ арқылы шешімдері ξ=ξ(x,y), ŋ=ŋ(x,y)
(2) бар.
(1)
функциялары анықталған деп ұйғарамыз,
яғни (1) функциялары G
аймағын
аймағына
бейнелеуді
анықтайды.Сонымен бірге бұл бейнелеу
мына шарттарды қанағаттандырады деп
ұйғарамыз: 1) Бейнелеу өзара бір мәнді,
яғни G аймағының әр түрлі нүктелеріне
міндетті
түрде D
аймағының
әр түрлі нүктелері сәйкес келеді. Басқаша
айтқанда,
теңдеулердің
бүкіл D аймағында
бірмәнді анықталған ξ
және ŋ арқылы шешімдері ξ=ξ(x,y), ŋ=ŋ(x,y)
(2) бар.
2)(1) (2) функциялар үзіліссіз және олардың бірінші ретті үзіліссіз туындылары бар.
3) Функциялық анықтауыш (якобиан)
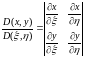 (3)
бүкіл Gаймағында
нөлден өзгеше, демек, бұл якобианға
енетін дербес туындылар үзіліссіздігі
ұйғарылғандықтан, G
аймағында таңбасы тұрақты. (2)
кері бейнелеу
якобианы
(3)
бүкіл Gаймағында
нөлден өзгеше, демек, бұл якобианға
енетін дербес туындылар үзіліссіздігі
ұйғарылғандықтан, G
аймағында таңбасы тұрақты. (2)
кері бейнелеу
якобианы
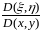 (3)
якобианмен былай
(3)
якобианмен былай
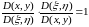 байланысқан. Сондықтан
байланысқан. Сондықтан
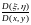 якобианы да еш жерде нөлге айналмайды.Егер
Gаймағында
жатық немесе құрама-жатық ξ=ξ(t)
якобианы да еш жерде нөлге айналмайды.Егер
Gаймағында
жатық немесе құрама-жатық ξ=ξ(t)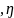 =
=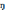 (t),
(t),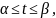 қисығы
берілсе, онда (1) бейнелеу оны жатық
немесе құрама-жатық
қисығы
берілсе, онда (1) бейнелеу оны жатық
немесе құрама-жатық
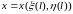 ,
,
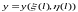 қисығына көшіреді, өйткені егер
қисығына көшіреді, өйткені егер
 туындылары бар және үзіліссіз болса,
онда
туындылары бар және үзіліссіз болса,
онда
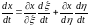 ,
,
 туындылары да бар және үзіліссіз әрі
бұлардың екеуі де бірден бірдей нөлге
айналмайды, тек
туындылары да бар және үзіліссіз әрі
бұлардың екеуі де бірден бірдей нөлге
айналмайды, тек
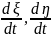 туындыларының ең болмағанда біреуі
нөлден өзгеше
болса болғаны (өйткені
туындыларының ең болмағанда біреуі
нөлден өзгеше
болса болғаны (өйткені
 ).
).
Сонда мұның дербес
жағдайы ретінде
 аймағының
Л шекарасы D
аймағының Г
шекарасына көшеді.Бұл тұжырым айқын
емес функциялар теориясынан шығады.
Егер Г қисығының (x0,y0)
нүктесіне D
аймағының
ішкі
аймағының
Л шекарасы D
аймағының Г
шекарасына көшеді.Бұл тұжырым айқын
емес функциялар теориясынан шығады.
Егер Г қисығының (x0,y0)
нүктесіне D
аймағының
ішкі
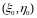 нүктесі
сәйкес болса, онда
нүктесі
сәйкес болса, онда
 ,
,
 теңдіктерінен
және
шамалары
теңдіктерінен
және
шамалары
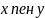
 пен
пен
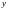 айнымалыларының функциялары ретінде
айнымалыларының функциялары ретінде
 нүктесінің белгілі бір маңайында
анықталған болар еді. Ал шекаралық
(x0,y0)
нүктесінің кез келген маңайында D
аймағында
жатпайтын да нүктелер бар, демек, G үшін
ішкі нүкте болатын (ξ0,ŋ0)
нүктесінің G жиынында жататын, бірақ D
аймағына
бейнеленбейтін маңайы табылады. Ал бұл
шарттқа қайшы.
нүктесінің белгілі бір маңайында
анықталған болар еді. Ал шекаралық
(x0,y0)
нүктесінің кез келген маңайында D
аймағында
жатпайтын да нүктелер бар, демек, G үшін
ішкі нүкте болатын (ξ0,ŋ0)
нүктесінің G жиынында жататын, бірақ D
аймағына
бейнеленбейтін маңайы табылады. Ал бұл
шарттқа қайшы.
20. Бірінші текті қисықсызықты интеграл
Айталық,
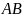 жазықтығы белгілі бір жатық немесе
құрама-жатық қисық,ал
жазықтығы белгілі бір жатық немесе
құрама-жатық қисық,ал
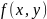 осы қисықта берілген функция болсын.
Осы қисық
осы қисықта берілген функция болсын.
Осы қисық
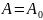 ,
,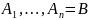 нүктелері арқылы
нүктелері арқылы
 бөліктерге бөліктеуін қарастырып, әрбір
бөліктерге бөліктеуін қарастырып, әрбір
 доғасынан кез келген бір
доғасынан кез келген бір
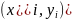 нүктесін алып,
нүктесін алып,
 (1) қосындысын
түзейік, мұнда
(1) қосындысын
түзейік, мұнда
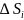 арқылы
доғасының
ұзындығы белгіленген.Егер
арқылы
доғасының
ұзындығы белгіленген.Егер
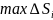 нөлге ұмтылғанда
интегралдың белгілі бір
нөлге ұмтылғанда
интегралдың белгілі бір
 ақырлы шекке ұмтылса,онда бұл шек
функциясының
қисығы бойынша бірінші
текті қисық сызықты интегралы
деп аталады және
ақырлы шекке ұмтылса,онда бұл шек
функциясының
қисығы бойынша бірінші
текті қисық сызықты интегралы
деп аталады және
 (2)
арқылы белгіленеді.Ескерту.
Мұнда
(2)
арқылы белгіленеді.Ескерту.
Мұнда
 және
және
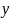 айнымалылары тәуелсіз айнымалылары
емес,
қисығының бойында жату шартымен
байланысқан нүктелер.Бірінші текті
қисықсызықты интеграл ұғымының бір
айнымалының функциясының анықталған
интегралынан өзгешелігі жоқ дерлік
және ерлік оған оңай келтіріледі. Шынында
да,
қисығынан параметр үшін бастапқы
нүктесінен есептелетін
айнымалылары тәуелсіз айнымалылары
емес,
қисығының бойында жату шартымен
байланысқан нүктелер.Бірінші текті
қисықсызықты интеграл ұғымының бір
айнымалының функциясының анықталған
интегралынан өзгешелігі жоқ дерлік
және ерлік оған оңай келтіріледі. Шынында
да,
қисығынан параметр үшін бастапқы
нүктесінен есептелетін
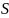 доға ұзындығын алып, бұл қисықты
доға ұзындығын алып, бұл қисықты (3)
(3)
теңдеулері арқылы
жазсақ,
қисығында берілген
функциясы
айнымалысының
 (
(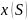 ,
, функциясына көшеді. Сонда
нүктесіне сәйкес
параметрінің мәнін
функциясына көшеді. Сонда
нүктесіне сәйкес
параметрінің мәнін
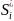 арқылы белгілеп, (1) интегралдық
қосындыны
арқылы белгілеп, (1) интегралдық
қосындыны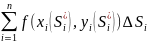 (4)түрінде
жазсақ, ол
(4)түрінде
жазсақ, ол анықталған
интегралына сәйкес интегралдық қосынды.Ал
(1) және (4) тең болғандықтан оларға сәйкес
интегралдар да тең, яғни
анықталған
интегралына сәйкес интегралдық қосынды.Ал
(1) және (4) тең болғандықтан оларға сәйкес
интегралдар да тең, яғни (5)
(5)
Бұл екі интегралдың бар болуы да, бар болмауы да бірдей. Сондықтан функциясы қисығы бойында үзіліссіз болса, онда (2) қисықсызықты интеграл бар.
21. Параметрлік
түрде берілген қисыққы берілген функ.
1-ші текті қисық сызықты интег.теорема.
Егер AB
 теңдеулері
арқылы берілген жатық қисық, ал
осы қисықта берілген функция болса,
онда
теңдеулері
арқылы берілген жатық қисық, ал
осы қисықта берілген функция болса,
онда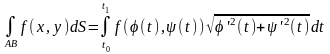 (1)теңдігі
орындалады әрі мұның сол жағындағы
қисықсызықты интеграл бар сонда және
тек сонда, егер оның оң жағындағы
анықталған интеграл бар болса.Мысалы,
егер AB қисығы
(1)теңдігі
орындалады әрі мұның сол жағындағы
қисықсызықты интеграл бар сонда және
тек сонда, егер оның оң жағындағы
анықталған интеграл бар болса.Мысалы,
егер AB қисығы
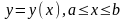 теңдеуі
арқылы берілсе, онда (1) формула
теңдеуі
арқылы берілсе, онда (1) формула
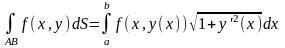 түрінде
жазылады.Ескерту.
Бірінші текті қисықсызықты интегралдың
екі айнымалы үшін анықталған анықтамасы
сөзбесөз кеңістіктік қисық бойында
берілген функция үшін де көшіріледі:
егер AB қисығы
түрінде
жазылады.Ескерту.
Бірінші текті қисықсызықты интегралдың
екі айнымалы үшін анықталған анықтамасы
сөзбесөз кеңістіктік қисық бойында
берілген функция үшін де көшіріледі:
егер AB қисығы
 параметрлік
теңдеулері арқылы берілсе, онда осы
қисық арқылы алынған бірінші текті
қисықсызықты интеграл
параметрлік
теңдеулері арқылы берілсе, онда осы
қисық арқылы алынған бірінші текті
қисықсызықты интеграл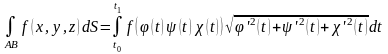
формуласы арқылы анықталған интегралға келтіріледі
22.Екінші текті
қисықсызықты интеграл және оның бірінші
текті қисықсызықты интегралмен
байланысыАйталық,
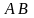 жазықтықтың жатық қисығы, ал
жазықтықтың жатық қисығы, ал
 осы
қисық бойында анықталған вектор-функция
болсын. Бұл қисықты координаттары
осы
қисық бойында анықталған вектор-функция
болсын. Бұл қисықты координаттары
 болатын
болатын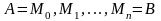 нүктелері
арқылы бөліктерге бөлейік те
нүктелері
арқылы бөліктерге бөлейік те
 қосындысын түзейік, мұндағы
қосындысын түзейік, мұндағы
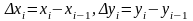 .
Егер
.
Егер
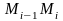 доғалары ұзындықтарының максимумы
нөлге ұмтылғанда (1) қосынды ақырлы бір
шекке ұмтылса, онда бұл шекті F=(P,Q)
вектор-функциясының AB қисығы бойынша
екінші текті
қисықсызықты интегралы
деп атайды да
доғалары ұзындықтарының максимумы
нөлге ұмтылғанда (1) қосынды ақырлы бір
шекке ұмтылса, онда бұл шекті F=(P,Q)
вектор-функциясының AB қисығы бойынша
екінші текті
қисықсызықты интегралы
деп атайды да
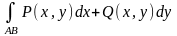 (2)
арқылы белгілейді.Екінші
текті қисықсызықты интеграл бірінші
текті қисықсызықты интегралға
оңай келтірілетінін мына теоремадан
көреміз:теорема.
Егер AB жатық қисығы
(2)
арқылы белгілейді.Екінші
текті қисықсызықты интеграл бірінші
текті қисықсызықты интегралға
оңай келтірілетінін мына теоремадан
көреміз:теорема.
Егер AB жатық қисығы (3)теңдеуі
арқылы берілген, ал F=(P,Q) вектор-функциясы
осы қисықта анықталған және шектеулі
болса, онда
(3)теңдеуі
арқылы берілген, ал F=(P,Q) вектор-функциясы
осы қисықта анықталған және шектеулі
болса, онда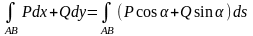 (4)
теңдігі орындалады. Мұнда
(4)
теңдігі орындалады. Мұнда арқылы AB қисығына М нүктесінде жүргізілген
жанама менхосінің
оң бағыты арасындағы бұрыш белгіленген.
Сонымен бірге, екінші текті қисықсызықты
интеграл бар, егер
оңжағындағы
бірінші текті қисықсызықты интеграл
бар болса.Дәлелдеу.
Ең алдымен
арқылы AB қисығына М нүктесінде жүргізілген
жанама менхосінің
оң бағыты арасындағы бұрыш белгіленген.
Сонымен бірге, екінші текті қисықсызықты
интеграл бар, егер
оңжағындағы
бірінші текті қисықсызықты интеграл
бар болса.Дәлелдеу.
Ең алдымен теңдігін
дәлелдейік.
теңдігін
дәлелдейік.
 интегралы анықтама бойынша
интегралы анықтама бойынша
 түріндегі
қосындының шегі. Осы қосындыны AB қисығының
дәл сол бөліктеуінде
түріндегі
қосындының шегі. Осы қосындыны AB қисығының
дәл сол бөліктеуінде
 интегралына сәйкес
интегралына сәйкес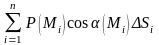 интегралдық
қосындысымен салыстырамыз.Егер x=x(s)
болса, онда АВ қисығының әрбір М нүктесінде
интегралдық
қосындысымен салыстырамыз.Егер x=x(s)
болса, онда АВ қисығының әрбір М нүктесінде
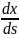 =
=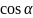 (M), демек,
(M), демек,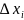 =
=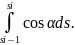
Eнді бұған орта
мән туралы теореманы қолдансақ =
= )
) мұнда
мұнда
 арқылы
арқылы
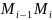 доғасының белгілі бір нүктесін
белгіледік.Сонда
доғасының белгілі бір нүктесін
белгіледік.Сонда Жатық
қисық бойында
Жатық
қисық бойында
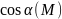 үзіліссіз, ал қисық тұйық шектеулі жиын
болғандықтан бұл функция бірқалыпты
үзіліссіз.Демек,кезкелген
үзіліссіз, ал қисық тұйық шектеулі жиын
болғандықтан бұл функция бірқалыпты
үзіліссіз.Демек,кезкелген
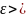 0
саны үшін АВқисығының жеткілікті майда
бөліктері үшін
0
саны үшін АВқисығының жеткілікті майда
бөліктері үшін Сонда
Сонда мұндағы
C=sup
мұндағы
C=sup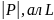 арқылы АВ қисығының ұзындығы
белгіленген.Мұнан
арқылы АВ қисығының ұзындығы
белгіленген.Мұнан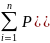 )
)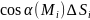 интегралдық
қосындысының шегі бар болса,онда
)
интегралдық
қосындысының шегі бар болса,онда
)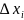 қосындысының
да сол шекке ұмтылатынын көреміз.Теорема
дәлелденді.
қосындысының
да сол шекке ұмтылатынын көреміз.Теорема
дәлелденді.
23. Параметрлік
қисықты берілген функциялық 2-ші текті
қисықсызықты интегралы. Егер
АВ қисығы x=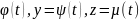 параметрлік теңдеулері арқылы берілсе
және А нүктесі үшін t=
параметрлік теңдеулері арқылы берілсе
және А нүктесі үшін t= ,ал
В нүктесі үшін
,ал
В нүктесі үшін
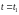 мәндері сәйкес болса,онда екінші текті
қисықсызықты интегралды
мәндері сәйкес болса,онда екінші текті
қисықсызықты интегралды

 теңдігі арқылы
анықталған интегралға келтіреді. P
теңдігі арқылы
анықталған интегралға келтіреді. P өрнегі
өрнегі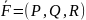 векторының АВ қисығына жүргізілген
жанамаға проекциясы болғандықтан оны
векторының АВ қисығына жүргізілген
жанамаға проекциясы болғандықтан оны
 арқылы белгілеп, дәл жазық жағдайдағыдай
арқылы белгілеп, дәл жазық жағдайдағыдай
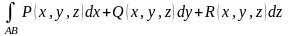 қисықсызықты
интегралды
қисықсызықты
интегралды
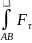 ds
ds
түрінде де жазады.
24. Грин
формуласы
.теорема.
Егер шекарасы Г болатын Д жәй тұйық
аймағында P(x,y),Q(x,y)функциялары
мен олардың
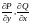 дербес туындылары үзіліссіз болса,онда
Грин формуласы деп аталатын
дербес туындылары үзіліссіз болса,онда
Грин формуласы деп аталатын 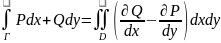
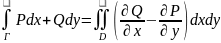 (1) формуласы орынды.Дәлелдеу.Төменнен
және жоғарыдан сәйкес y=
(1) формуласы орынды.Дәлелдеу.Төменнен
және жоғарыдан сәйкес y=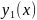 ,y=
,y=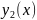 (2)құрама
жатық қисықтарымен,ал сол және оң
жақтарынан x=a,x=b (3) түзулерімен қоршалған
қарапайым Д аймағы үшін жүргізейік.Бұл
аймақтың АВСДА шекарасын оң бағытталған
деп есептейміз,яғни оның бойымен
жылжығанда суретте көрсетілгендей Д
аймағы сол жақта қалып отыратындай
бағыт алынған. Енді
(2)құрама
жатық қисықтарымен,ал сол және оң
жақтарынан x=a,x=b (3) түзулерімен қоршалған
қарапайым Д аймағы үшін жүргізейік.Бұл
аймақтың АВСДА шекарасын оң бағытталған
деп есептейміз,яғни оның бойымен
жылжығанда суретте көрсетілгендей Д
аймағы сол жақта қалып отыратындай
бағыт алынған. Енді
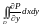 екі еселі интегралын қисықсызықты
интегралға түрлендірейік.Ол үшін
оны қайталанбалы интегралға келтірейік:
екі еселі интегралын қисықсызықты
интегралға түрлендірейік.Ол үшін
оны қайталанбалы интегралға келтірейік:
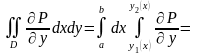
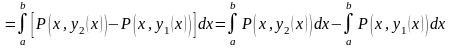 (4)
Бұлардың әрқайсысын қисық сызықты
интеграл деп қарастыруға болады:
(4)
Бұлардың әрқайсысын қисық сызықты
интеграл деп қарастыруға болады:
 ,
,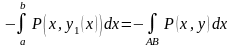 Әрқайсысы нөлге тең болатын
Әрқайсысы нөлге тең болатын
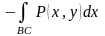 және
және
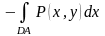 екі қисықсызықты интегралдарын
оң
жағына қоссақ, онда
екі қисықсызықты интегралдарын
оң
жағына қоссақ, онда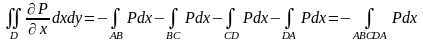 (5)теңдігін
аламыз. Енді х және у рөлдерін ауыстырып,
(5)теңдігін
аламыз. Енді х және у рөлдерін ауыстырып,
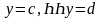 горизонталь кесінділерімен және
горизонталь кесінділерімен және
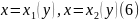 қисықтарымен қоршалған
қисықтарымен қоршалған
 аймағын алып және ол аймақ бойынша
алынған
аймағын алып және ол аймақ бойынша
алынған
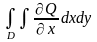 екі еселі интегралын
екі еселі интегралын
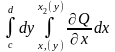 түрінде жазып, (5)теңдікті дәлелдегендей
есептеулер жүргізіп,
түрінде жазып, (5)теңдікті дәлелдегендей
есептеулер жүргізіп,
 (7)
(7)
теңдігін аламыз.
Шынында да, шекарасы Г болатын Д аймағы
әрқайсысында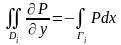
 теңдіктері
орындалатын
теңдіктері
орындалатын
 ,
, (шекаралары
(шекаралары
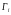 )
бөліктерге бөлінсін.
Бұларды қосындылап, сол жағынан Д аймағы
бойынша алынған екі еселі интегралды,
ал оң жағынан Гi контурлары арқылы
алынған қисық сызықты интегралдар
қосындысын аламыз. Бұл контурлардың
әрқайсысы Д аймағын қоршайтын қисықтардан
және Д аймағын бөліктейтін қосымша
сызықтардан тұрады. Бірақ, бұл қосымша
сызықтардың әрқайсысы Гi құрамына дәл
екі рет кіреді; Демек, олардың әрқайсысы
арқылы қисықсызықты интеграл екі рет
алынады және қарама-қарсы бағытта ,
сондықтан да
)
бөліктерге бөлінсін.
Бұларды қосындылап, сол жағынан Д аймағы
бойынша алынған екі еселі интегралды,
ал оң жағынан Гi контурлары арқылы
алынған қисық сызықты интегралдар
қосындысын аламыз. Бұл контурлардың
әрқайсысы Д аймағын қоршайтын қисықтардан
және Д аймағын бөліктейтін қосымша
сызықтардан тұрады. Бірақ, бұл қосымша
сызықтардың әрқайсысы Гi құрамына дәл
екі рет кіреді; Демек, олардың әрқайсысы
арқылы қисықсызықты интеграл екі рет
алынады және қарама-қарсы бағытта ,
сондықтан да
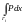 түріндегі интегралдарды
түріндегі интегралдарды
қосындылауда
қосымша сызықтар арқылы алынған
интегралдар өзара нольге тең болады
да, тек Д аймағының шекарасы арқылы
алынған интегралдар ғана қалады, яғни
біз
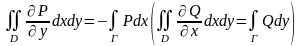 (8)
теңдігін аламыз, мұндағы Г Д аймағының
оң бағытталған шекарасы.
(8)
теңдігін аламыз, мұндағы Г Д аймағының
оң бағытталған шекарасы.
Сонымен қарапайым
аймақ үшін, дәлелдеуіміз бойынша,(8)
формулалар орынды. Енді оларды бірінен
бірін шегеріп
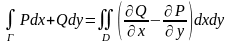 Гринформуласын
аламыз.
Гринформуласын
аламыз.
