13. Үзіліссіз функция графигінің өлшемінің нөлге теңдігі

Теорема. [a,b] кесіндісінде үзіліссіз f(x) функциясының графигінің өлшемі нөлге тең.Дәлелдеу. Вейерштрасс теоремасы бойынша бұл функция [a,b] кесіндісінде шектеулі, яғни m≤f(x)≤MДемек, оның графигі 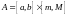тіктөртбұрышында жатады. Енді санын алып,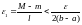 (1)болатындай етіп, l санын таңдайық.[a,b] кесіндісінде үзіліссіз функциясы бұл кесіндіде бірқалыпты үзіліссіз. Сондықтан, ε₁ санына сәйкес 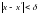шартын қанағаттандыратын [a,b] кесіндісінің x, x’ нүктелері үшін

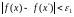(2) теңсіздігі орындалатын 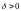оң саны табылады. Енді А тіктөртбұрышының , , 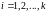(3)болатын Р бөлшектеуін түзейік. Онда (1),(2),(3) бойынша функциясының графигімен ортақ нүктелері бар Р бөлшектеуінің тіктөртбұрыштары аудан­дарының қосындысы үшін бағалауын аламыз. Сонда Жордан өлшемінің нөлге теңдігі туралы теорема бойынша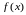 функциясының графигінің өлшемі нөл.

14. Түзуленетін қисық өлшемінің нөлге теңдігі

Теорема. Кез келген түзуленетін қисық өлшемі нөлге тең.Дәлелдеу. Айталық, Г- түзуленетін контур, ал |Г| оның ұзындығы болсын. Бұл қисықты к+1 нүктелер арқылы әрқайсысының ұзындығы -ден аспай­тындай етіп бөлшектейік және бұл нүктелердің әрқайсысын қабырғалары шаршы центрі етіп алайық. 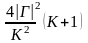Бұл шаршылардың бірігуі Г қисығын қоршайтын көпбұрышты фигура болады да, оның ауданы шаршы аудандарының қосындысынан, яғни -ден аспайды. Ал |Г|- белгілі бір сан болған­дықтан к санын Г қисығы, шынында да, ауданы жеткілікті аз болатын фигура ішінде жататындай етіп таңдап алуға болады. Демек, Жордан өлшемінің нөлге теңдігі туралы теорема бойынша Г қисығының өлшемі нөлге тең.

15. Үзіліссіз функция интегралдануы1-теорема. Тұйық шектеулі өлшемді Д жиынында үзіліссіз функция осы жиында интегралданады.Дәлелдеу. Тұйық шектеулі жиында үзіліссіз функциясы осы жиында шектеулі және бірқалыпты үзіліссіз болғандықтан, кез келген саны үшін Д жиынының диаметрлері -дан кіші жиындарында функция­сының M_ij және m_ijмәндерінің айырымы ε-нен кіші болатын (яғни M_ij-m_ij<ε) саны табылады. Сондықтан,

Демек, функциясы интегралданады.Ескерту. Функцияның үзіліссіздігі тым артық талап. Оны жеңілдетуге болады.2-теорема. Егер f(x,y) функциясы өлшемді тұйық шектеулі Д жиынында шектеулі және Д аймағының өлшемі нөлге тең жиындарынан басқа жерінде үзіліссіз болса, онда ол Д аймағында интегралданады.

16.Тіктөртбұрышты аймақ жағдайында еселі интегралды қайталанба интегралға келтіру. Алдымен қабырғалары координат остеріне параллель тіктөртбұрыш бойынша алынған еселі интегралды қарастырайық.

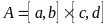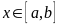теорема.Егер тіктөртбұрышында анықталған функциясы үшін ₍₁₎екі еселі интегралы, ал әрбір үшін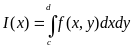 ₍₂₎интегралы бар болса, онда 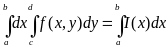₍₃₎интегралы да бар және теңдігі орынды.Дәлелдеу. А тіктөрбұрышына Р =(Р₁,Р₂) бөліктеуін жасаймыз. Мұндағы кесіндісінің бөліктеуі, ал Р₂ = {c = y₀ ≤y₁≤…≤y_l= d} [c,d] кесіндісінің бөліктеуі. Онда А_ij тіктөртбұрышында

.Енді осы теңсіздіктерді у арқылы у_j-ден у_j+1-ге дейін интегралдап теңсіздіктерді аламыз. Мұндағы 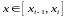. Егер 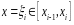деп j бойынша 1 ден 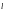-ге дейін қосындыласақ 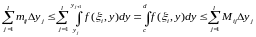яғни . (4)Мұны ∆x_i-ге көбейтіп, і арқылы 1-ден к-ге дейін қосындыласақ,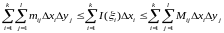 (5)

Бұлардың 1-ші және соңғы қосындылары 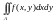екі еселі интеграл үшін сәйкес төменгі және жоғарғы қосындылар.Егер (5) теңсіздіктерде Р бөлшектеуінің диаметрін нөлге ұмтылдырып шекке көшсек (әрине, онда max ∆x_i→0), .Демек, (3) қайталанба интегралы бар және Ескерту. Егер х және у рөлдерін ауыстырып және 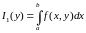интегралы бар деп ұйғарсақ, онда дәл(4)сияқты теңдігін аламыз.Ал егер (1) екі еселі интегралымен бірг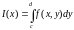е және интегралдарының екеуі де бар болса,онда

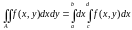
17. Қисық сызықты аймақ жағдайы. Айталық, екі үзіліссіз және 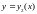қисықтарымен және x = a, x = b вертикаль түзулерімен шектелген аймақ болсын.теорема. Егер Д аймағында анықталған функциясы үшін .екі еселі интегралы бар, ал әрбір үшін 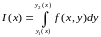интегралы бар болса, онда

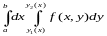
қайталанба интегралы да бар және 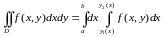(1)

теңдігі орынды.

Дәлелдеу үшін D жиынын ұстайтын 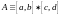тіктөртбұрышын алайық.

Онда екі еселі интеграл анықтамасы бойынша 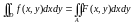(2)

Мұндағы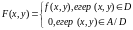 Сонда әрбір үшін

(3)екені айқын.Ал теңдік

бойынша ₍₄₎Демек, (2)-(4) теңдіктерден