40.Стокс формуласы
теорема.
Егер P(x,y,z), Q(x,y,z), R(x,y,z) функциялары
контурымен қоршалған бағытталған
беті
жататын аймақта анықталған және біріші
ретті туындыларымен бірге осы аймақта
үзіліссіз болса,онда Стокс формуласы
деп аталатын
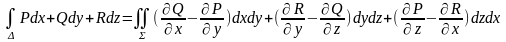(1)
формуласы орынды.Дәлелдеу. Алдымен интегралдың оң жағын былай
(2)түрінде
жазып, мұның бірінші қосылғышын жеке
қарастырайық.Айталық,
беті Декарт координаттарында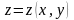
теңдеуі
арқылы берілсін.
арқылы
бетінің
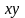жазықтығына проекциясын және
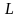арқылы оның шекарасын, яғни
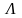контурының проекциясын белгілейік
(суретті қараңыз).Біз
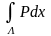қисықсызықты интегралын қарастырып,
кеңістік
контурының
теңдеуімен берілген
бетінде жатқандығынан оны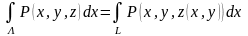
жазықтық
контуры бойынша алынған қисық сызықты
интегралға түрлендіреміз. Сонан соң
Грин формуласын қолданып оны
аймағы бойынша алынған екі еселі
интегралда келтірtміз. Мұнда
функциясының x
және y
айнымалыларының күрделі функциясы
екенін және оның yбойынша
туындыны есептеуде ескердік. Нормальдік
бағыттаушы косинустары өрнектерін
пайдаланып,
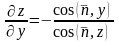теңдігін
аламыз, сонда
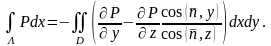Енді
бойынша екі еселі интегралынан
бойынша интегралына көшеміз:
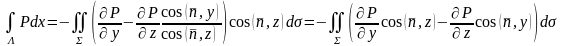.Сонымен,
(3)Біз
формуланы табуда
беті
түрінде берілген деп ұйғардық. Дәл
осындай нәтижеге
бетінің
теңдеуі
арқылы берілген жағдайында да жетуге
болады. Ол үшін
бетінің
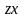жазықтығына
(
жазықтығына емес) проекциясын қарастырып,
дәл жоғарыдағыдай дәлелдеу жүргізуге
болады. Ал, егер
өсіне перпендикуляр жазықтық бөлігі
болса (әрине, онда ондай
бетті
жазықтығына да,
жазықтығына
да бірмәнді проекциялауға болмайды),
онда (3) түрдегі теңдік мардымсыз түрде
орынды (тривиальным образом): оның оң
жағы да, сол жағы да нөлге тең. Енді Грин
және Остроградский формулаларын
дәлелдеуде қолданған стандарттық әдіс
әрқайсысында (3) формула орындалатын
саны ақырлы беттерге жіктелетін
беті үшін де орынды. Сонымен, (3) теңдіктің
дұрыстығы жоғарыда келтірілген беттер
түріндегі саны ақырлы беттер кесектері
үшін де орынды екен. Сонымен, дәл
жоғарыдағы (3) теңдік сияқты дәлелденетін
,(4)
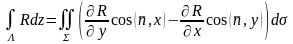(5)теңдіктерін
аламыз. Бұл (3)-(5) теңдіктерді қосып,
дәлелдеу керек
(2) формуланы аламыз. Міне осы формуланы Стокс формуласы деп атайды. Кейде Стокс формуласы деп (1) формулаyы да айтады.