2.2 Критерий кратности корней.

Теорема. Элемент является корнем многочлена кратности 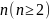тогда и только тогда, когда и он является корнем кратности 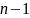у производной многочлена .

Доказательство.

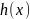Необходимость. Пусть - корень кратности многочлена , тогда по определению , где не делится на . Применим теорему ( для любых многочленов 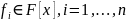, и любого натурального справедливо равенство 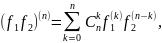где обозначает ).

Отсюда имеем, что

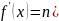
Следовательно, 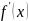делится 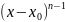на , но не делится на , так как не делится на .

Достаточность. Пусть и 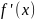делится . Докажем, что – корень кратности многочлена 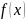. Предположим, что , где не делится на . Тогда

многочлен не делится на и, следовательно, является корнем кратности 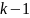производной , откуда . ([2],с.152)

Любой многочлен может быть единственным образом разложен по степеням

Это легко доказывается индукцией по степени многочлена. Действительно, разделим на 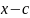с остатком. Получим

,

где 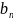– остаток, 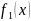– многочлен степени . В силу индуктивного предположения

,

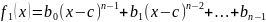откуда .

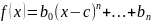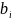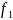Опишем алгоритм для вычисления коэффициентов . Свободный член разложения есть остаток от деления на , есть остаток при делении неполного частного на , и вычисление последующих коэффициентов требует вычисления неполного частного 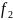при делении на . Далее, находится как остаток при делении на и т.д.

Красивые формулы для коэффициентов указывает следующая теорема.

Теорема(Тейлор). Любой многочлен степени можно представить в виде

.

Доказательство. Пусть .

Продифференцируем раз обе части этого равенства. Используя правила дифференцирования, получаем, что

Полагая 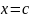, имеем . ([2],с.153)

2.3 Схема Горнера.

Деление произвольного многочлена на двучлен может быть выполнено существенно проще, чем деление на произвольный многочлен.

Действительно, если нужно разделить многочлен

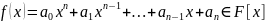
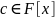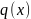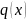на двучлен , где , т.е. найти такие и , что , , и , естественно искать в форме 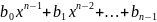. Тогда получим равенство

равносильное цепочке равенств

,

,

,

……………………

,

,

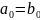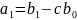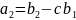откуда последовательно определяются коэффициенты и остаток :

,

,

,

……………………

,

.

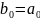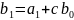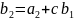Заметим, что остаток равен значению 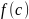многочлена при .

Действительно, переходя в равенстве к значениям при , получим 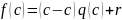, откуда .

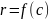Указанный способ вычисления коэффициентов частного и остатка носит название схемы Горнера. ([2],с.154-155)

Пример 1. Разложить многочлен по степеням .

Применим схему Горнера.

1	0	0	0	0	0
1	2	4	8	16	32
1	4	12	32	80
1	6	24	80
1	8	40
1	10
1

Остатки подчёркнуты.

Таким образом, .

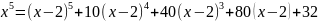Для приближённого вычисления корней многочлена бывает нужно найти одновременно и . Выполнить это можно при помощи схемы Горнера, вычислив два коэффициента разложения по степеням .

Пример 2.

Для многочлена вычислить 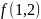и .

Применим схему Горнера.

1	0	-1	-1
1	1,2	0,44	-0,472
1	2,4	3,32

Итак, и .