
- •Глава 1. Дискриминанты и результанты многочленов 4
- •Глава 2. Кратные корни многочлена 10
- •Введение
- •Глава 1. Дискриминанты и результанты многочленов
- •1.1 Результант.
- •1.2 Дискриминант.
- •1.3 Вычисление некоторых результантов и дискриминантов.
- •Глава 2. Кратные корни многочлена
- •2.1 Понятие корня и кратного корня.
- •2.2 Критерий кратности корней.
- •2.3 Схема Горнера.
- •Список использованной литературы
Оглавление
Введение 2
Глава 1. Дискриминанты и результанты многочленов 4
1.1 Результант. 4
1.2 Дискриминант. 6
1.3 Вычисление некоторых результантов и дискриминантов. 7
Глава 2. Кратные корни многочлена 10
2.1 Понятие корня и кратного корня. 10
2.2 Критерий кратности корней. 10
2.3 Схема Горнера. 11
Список использованной литературы 14
Введение
Способ нахождения корней линейных и квадратичных многочленов, то есть способ решения линейных и квадратных уравнений, был известен ещё в древнем мире. Поиски формулы для точного решения общего уравнения третьей степени продолжались долгое время, пока не увенчались успехом в первой половине XVI века в трудах Сципиона дель Ферро, Никколо Тарталья и Джероламо Кардано. Формулы для корней квадратных и кубических уравнений позволили сравнительно легко получить формулы для корней уравнения четвертой степени.
То, что корни общего уравнения пятой степени и выше не выражаются при помощи рациональных функций и радикалов от коэффициентов, было доказано норвежским математиком Нильсом Абелем в 1826 году.Это совсем не означает, что корни такого уравнения не могут быть найдены. Во-первых, в частных случаях, при некоторых комбинациях коэффициентов, корни уравнения всё же могут быть определены. Во-вторых, существуют формулы для корней уравнений 5-й степени и выше, использующие специальные функции — эллиптические или гипергеометрические.([1],с.192)
В случае, если все коэффициенты многочлена рациональны, то нахождение его корней приводится к нахождению корней многочлена с целыми коэффициентами. Для рациональных корней таких многочленов существуют алгоритмы нахождения перебором кандидатов с использованием схемы Горнера.
Актуальность данной курсовой работы заключается в том, что решение квадратных уравнений с помощью дискриминанта, нахождение корней уравнений с помощью схемы Горнера находит широкое применение в школе.
Объектом данной курсовой работы являются понятия «дискриминант, результант и кратные корни».
Предмет исследования – анализ теоретического материала.
Цель курсовой работы – исследование и анализ нахождения корней многочленов.
Задачи:
- раскрыть сущность понятий «дискриминант, результант и кратные корни»;
- рассмотреть свойства и способы вычисления дискриминантов и результантов;
- выявить связь между понятиями «дискриминант, результант и кратные корни многочленов»;
- рассмотреть способ нахождения кратных корней.
Глава 1. Дискриминанты и результанты многочленов
1.1 Результант.
Рассмотрим
многочлены
 и
и
 ,
где
,
где
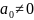 и
и
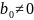 .
Над алгебраически замкнутым полем
многочлены
.
Над алгебраически замкнутым полем
многочлены
 и
и
 имеют общий делитель тогда и только
тогда, когда они имеют общий корень.
Если же поле не алгебраически замкнуто,
то общий делитель может быть многочленом,
не имеющим корней.([3],с.30)
имеют общий делитель тогда и только
тогда, когда они имеют общий корень.
Если же поле не алгебраически замкнуто,
то общий делитель может быть многочленом,
не имеющим корней.([3],с.30)
Наличие
у
и
общего делителя эквивалентно тому, что
существуют такие многочлены
 и
и
 ,
что
,
что
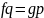 ,
причём
,
причём
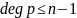 и
и
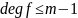 .
Пусть
.
Пусть
 и
и
 .
Равенство
можно записать в виде системы уравнений
.
Равенство
можно записать в виде системы уравнений
 ,
,
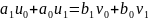 ,
,
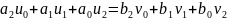 ,
,
………………………………………………..
Многочлены
и
имеют общий корень тогда и только тогда,
когда эта система имеет ненулевое
решение
 .
Если, например,
.
Если, например,
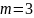 и
и
 ,
то определитель этой системы уравнений
имеют вид
,
то определитель этой системы уравнений
имеют вид
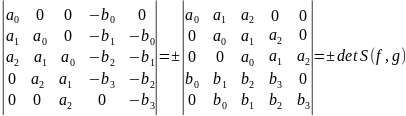 .
.
Матрицу
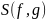 называют матрицей Сильвестра многочленов
и
.
Определитель матрицы
называют результантом многочленов
и
;
результант многочленов
и
обозначают
называют матрицей Сильвестра многочленов
и
.
Определитель матрицы
называют результантом многочленов
и
;
результант многочленов
и
обозначают
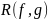 .
Ясно, что
– однородный многочлен степени
.
Ясно, что
– однородный многочлен степени
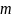 по переменным
по переменным
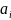 и степени
и степени
 по переменным
по переменным
 .
Многочлены
и
имеют общий делитель тогда и только
тогда, когда определитель рассматриваемой
системы равен нулю, т. е.
.
Многочлены
и
имеют общий делитель тогда и только
тогда, когда определитель рассматриваемой
системы равен нулю, т. е.
 .
.
Результант
имеет много разных приложений. Например,
если заданы полиномиальные соотношения
 и
и
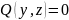 ,
то с помощью результанта можно получить
полиномиальное соотношение
,
то с помощью результанта можно получить
полиномиальное соотношение
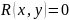 .
В самом деле, рассмотрим данные полиномы
.
В самом деле, рассмотрим данные полиномы
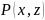 и
и
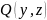 как полиномы от
как полиномы от
 ,
считая
,
считая
 и
и
 постоянными. Тогда результант
постоянными. Тогда результант
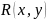 этих полиномов даст требуемое соотношение
.
этих полиномов даст требуемое соотношение
.
Результант
позволяет также сводить решение системы
алгебраических уравнений к нахождению
корней многочленов. В самом деле, пусть
 и
и
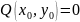 .
Рассмотрим
.
Рассмотрим
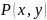 и
и
 как многочлены от
.
При
как многочлены от
.
При
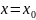 они имеют общий корень
они имеют общий корень
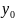 .
Следовательно, их результант
.
Следовательно, их результант
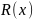 равен нулю при
.
([3],с.31)
равен нулю при
.
([3],с.31)
Теорема
1. Пусть
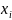 – корни многочлена
,
а
– корни многочлена
,
а
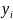 – корни многочлена
.
Тогда
– корни многочлена
.
Тогда
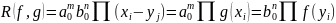 .
.
Доказательство.
Так как
 ,
то
,
то
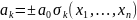 ,
где
,
где
 – элементарная симметрическая функция.
Аналогично
– элементарная симметрическая функция.
Аналогично
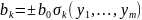 .
Результант является однородным
многочленом степени
по переменным
и степени
по переменным
,
поэтому
.
Результант является однородным
многочленом степени
по переменным
и степени
по переменным
,
поэтому
 ,
,
где
 – симметрический многочлен от
– симметрический многочлен от
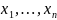 и
и
 ,
обращающийся в нуль при
,
обращающийся в нуль при
 .
Формула
.
Формула

показывает, что
 .
.
Подставив
в это равенство
,
получим, что
 – нулевой многочлен. Аналогичные
рассуждения показывают, что многочлен
делится на
– нулевой многочлен. Аналогичные
рассуждения показывают, что многочлен
делится на
 .
.
Так
как
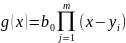 ,
то
,
то
 ,
а значит,
,
а значит,

-
однородный многочлен степени
по переменным
 .
Для переменных
.
Для переменных
 рассуждения аналогичны. Ясно также, что
симметрический многочлен
рассуждения аналогичны. Ясно также, что
симметрический многочлен
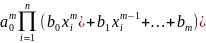 является многочленом от
является многочленом от
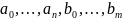 .
Следовательно,
.
Следовательно,
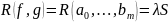 ,
где
,
где
 – некоторое число. С другой стороны,
коэффициент при
– некоторое число. С другой стороны,
коэффициент при
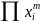 у многочленов
у многочленов
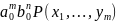 и
и
 равен
равен
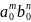 ,
поэтому
,
поэтому
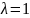 .
.

Следствие
1.
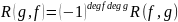 .
([3],с.32)
.
([3],с.32)
Следствие
2. Если
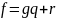 ,
то
,
то
 ,
,
где
 -
старший коэффициент многочлена
.
-
старший коэффициент многочлена
.
Доказательство.
Пусть
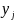 -
корни многочлена
.
Тогда
-
корни многочлена
.
Тогда
 .
Остаётся воспользоваться тем, что
.
Остаётся воспользоваться тем, что
 и
и
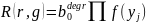 .
.
Следствие
3.
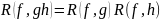 .
.
Доказательство.
Пусть
-
корни многочлена
,
а
 -
его старший коэффициент. Тогда
-
его старший коэффициент. Тогда
 ,
,
 ,
,
 .
.
Теорема
2. Пусть
и
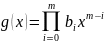 .
Тогда существуют многочлены
.
Тогда существуют многочлены
 и
и
 с целыми коэффициентами от переменных
с целыми коэффициентами от переменных
 ,
для которых выполняется равенство
,
для которых выполняется равенство
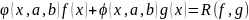 .
.
Доказательство.
Пусть
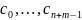 -
столбцы матрицы Сильвестра
и
-
столбцы матрицы Сильвестра
и
 .
Тогда
.
Тогда
 , где
, где
 – столбец (
– столбец ( .
Рассмотрим это равенство как систему
линейных уравнений относительно
.
Рассмотрим это равенство как систему
линейных уравнений относительно
 и воспользуемся правилом Крамера, чтобы
найти
и воспользуемся правилом Крамера, чтобы
найти
 .
В результате получим
.
В результате получим
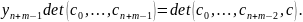 (1)
(1)
Остаётся
заметить, что
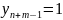 ,
,
 ,
а определитель, стоящий в правой части
равенства (1), можно представить в
требуемом виде.
([3],с.33)
,
а определитель, стоящий в правой части
равенства (1), можно представить в
требуемом виде.
([3],с.33)
