2. Абсолютные значения 1% прироста
=0,01*
=0,01*71,4=0,714
=0,01*47,7=0,477
=0,01*35,1=0,351
=0,01*18,3=0,183
3.Средний уровень ряда
=
= 43,13
4.Средний годовой темп роста Темп прироста
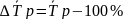
=0,54
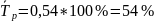
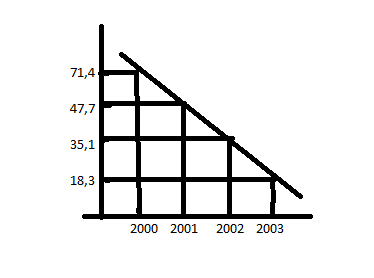
Вывод: Из графика видно, что происходит спад производства из-за уменьшения на производство продукции.
16. Товарные остатки по двум группам товаров на 1-ое число каждого месяца составили:
(тыс.
тг.)
-
Товарная группа
Дата
1 января
1февраля
1марта
1 апреля
1.Прoдовольственные товары
210
220
200
230
2.Непродовольственные товары
556
350
390
360
Всего:
766
570
590
590
Вычислить средний квартальный остаток:
по продовольственным товарам;
по непродовольственным товарам;
по обеим группам вместе.
Поясните, почему методы расчета средних уровней рядов динамики в задачах 4 и 5 различны.
Решение:
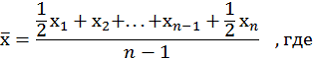(продов.тов)=210/2+220+200+230/2
=
105+420+115
=213.3
4-1 3
(непродов. тов)=556/2+350+390+360/2 =278+760+180 =399.3
4-1 3
(1,2)=766/2+570+590+590/2 =383+1160+295 =612.7≈613
3 3
Вывод: В данной задаче используем среднюю хронологическую, так как в условии даны моментные динамические ряды, то есть данные представлены на определенный период времени, и интервалы между датами равны. Средний квартальный остаток по непроизводственным товарам превысил средний квартальный остаток по производственным товарам на 186 тыс. тенге, а средний квартальный остаток по обеим группам составил 613 тыс. тенге.
Имеются следующие данные о товарообороте магазина:
Товарная группа |
Продано товаров в фактических ценах, тыс. тг. |
Процент изменения цен во 2 квартале по сравнению с 1 кварталом |
|
1 квартал (p0q 0) |
2 квартал (p1q1) |
||
1 |
48 |
92 |
+ 15 |
2 |
22 |
21 |
-6 |
3 |
29 |
18 |
без изменения |
Итого: |
99 |
131 |
- |
Вычислить:
индивидуальные и общий индексы цен;
общий индекс товарооборота в фактических ценах;
используя взаимосвязь индексов товарооборота и цен, вычислить общий индекс физического объема товарооборота;
сумму экономии или дополнительного расхода от изменения цен, полученную населением при покупке товаров в данном магазине.
Сделайте выводы.
Решение:
1)В данной задаче, чтобы определить общий индекс цен используем общий индекс цен в форме средней гармонической Пааше по формуле:
=
Для вычисления этого индекса определим предварительно индивидуальные индексы цен для каждой товарной группы:
ip=100+15=115%=1.15
ip=100-6=94%=0.94
ip=1
Ip= __ 131________=131/120.3=1.089=108.9% повышается на 8,9%
92/1.15+21/0.94+18/1
Товарооборот( количество проданных товаров) по данной товарной группе за 2 квартал в среднем увеличился на 8.9% за счет изменения цен.
2)Общий индекс товарооборота в фактических ценах:
Ipp=∑q1p1Q1/∑p0q0Q0=131/99=1.323=132.3% повышается на 32,3%
В денежном выражении: 131-99=32 тыс. тенге
Количество проданных товаров во 2 квартале по сравнению с 1 кварталом увеличился на 32,3%, а в денежном выражении это составило 32 тыс. тенге.
3)Используя взаимосвязь индексов товарооборота, цен и физического объема товарооборота определим общий индекс физического объема товарооборота , то есть количества проданного товара:
Ipq=Ip* Iq Iq=Ipq/Ip=1.323/0.96=1.38
4)∆p=131-120.3=10.7→сумма перерасхода ,полученная населением при покупке товара в данном магазине
Продажа сельскохозяйственных продуктов характеризуется следующими показателями:
Товарная группа |
Продано товаров, тыс. тг. |
Изменение количества проданных товаров в отчетном периоде по сравнению с базисным в % |
||
базисный период
(p0q0) |
отчетный период
(p1q1) |
|||
1 |
60 |
58 |
- 8 |
|
2 |
46 |
46 |
без изменения |
|
3 |
170 |
190 |
+ 18 |
|
Итого: |
276 |
294 |
- |
|
Вычислить: индивидуальные индексы и общий индекс физического объема товарооборота.
Сделайте выводы.
Решение:
Вычислим индивидуальные индексы:
1)100-8=92=0,92→ Ip=0,92 снижение цен на 8%
2)100-1=99=0,99→ Ip=1 без изменений, на том же уровне
3)100+18=118=1,18→ Ip=1,18 повышение цен на 18%
Общий индекс физического объема товарооборота ,то есть количества проданного товара :
Для этого используем взаимосвязь индексов товарооборота цен и физического объема товарооборота:
Ipq=∑q1p1Q1/∑p0q0Q0=294/276=1.065
Ip=_____294____ =294/63+46+161=294/270=1.089
58/0.92+46/1+190/1.18
Iq=Ipq/Ip=1.065/1.089=0.978
В заключении, можно сказать, что товарооборот в отчетном периоде увеличился на 6,5% ,за счет увеличения цен на 8,9% и снижения физического объема товарооборота на 2,2%.
19Динамика себестоимости и объема продукции характеризуются следующими данными:
Изделие |
Себестоимость единицы продукции, тыс.тг. |
Выработано продукции, единиц |
||
базисный период (z0) |
отчетный период (z1) |
базисный период (q0) |
отчетный период (q1) |
|
А |
1 |
2 |
3 |
4 |
Завод №1. М – 404 АТ – I Б – 405 |
15,0 9,0 14,0 |
15,7 9,2 13,6 |
3000 1500 1460 |
3500 1800 1600 |
Завод №2. АТ – I |
6,0 |
6,5 |
1700 |
1600 |
На основе этих данных определить:
для завода №1 по трем видам изделий вместе:
а) общий индекс затрат на продукцию;
б) общий индекс себестоимости продукции;
в) общий индекс физического объема выпущенной продукции;
г) покажите взаимосвязь между этими индексами;
для двух заводов вместе по одинаковым изделиям:
а) индекс себестоимости переменного состава;
б) индекс себестоимости фиксированного состава;
в) индекс структуры;
г) покажите взаимосвязь между этими индексами.
Поясните полученные результаты.
РЕШЕНИЕ:
для завода №1:
Общий индекс затрат на продукцию
Iq=
=
=
=
=1.154
1.154*100%= 115.4%
Общий индекс физического объема произведенной продукции
=
=
=
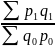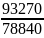= 1.181 *100%= 118.1%
С помощью взаимосвязи индексов можно вычислить общий индекс себестоимости
Сумма изменения затрат в отчетном периоде по сравнению с базисным:
=
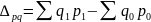(3500*15.7+1800*9.2+1600*13.6) -(3000*15.0+1500*9.0+1460*14.0) =
93270-78940= 14330 тенге.
Сумма изменения затрат в отчетном периоде по сравнению с базисным за счет изменения себестоимости составило:
93270-
(3500*15.0+1800*9.0+1600*14.0)= 93270-91100= 2170 тенге.
Сумма изменения затрат в отчетном периоде по сравнению с базисным за счет изменения физического объема продукции составило:
=
91100-78940= 12160 тенге.
Для 2 заводов:
-
№
Выработано продукции
Себестоимость
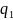
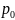
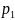
1
1500
1800
9.0
9.2
2
1700
1600
6.0
6.5
Индекс переменного состава представляет собой отношение двух взвешенных средних величин с переменным весом, харак-щие изменение индексируемого показателя:
=
= 1.07 * 100% = 107%
Индекс себестоимости постоянного состава представляет собой отношение двух взвешенных средних величин с одними и теми же весами:
=
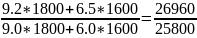= 1.044= 104.4%
Индекс структуры:
=
1.024= 102.4%
Разница между индексами постоянного и переменного состава объясняется использованием величин с постоянными весами в одном случае и переменными весами в другом.
Товарооборот и издержки обращения в 10 магазинах города за отчетный период характеризуются следующими данными:
Номер магазина |
Товарооборот, млн тг. (х) |
Издержки обращения,млн тг. (у) |
|
|
|
|
|
1 |
6 |
0,2 |
1,2 |
-10,2 |
-0,41 |
104,04 |
0,1681 |
2 |
5 |
0,5 |
2,5 |
-11,2 |
-0,11 |
125,44 |
0,0121 |
3 |
17 |
0,6 |
10,2 |
0,8 |
-0,01 |
0,64 |
0,0001 |
4 |
19 |
0,6 |
11,4 |
2,8 |
-0,01 |
7,84 |
0,0001 |
5 |
24 |
0,8 |
19,2 |
7,8 |
0,19 |
60,84 |
0,0361 |
6 |
13 |
0.7 |
9,1 |
-3,2 |
0,09 |
0,0081 |
0,0081 |
7 |
26 |
0,9 |
23,4 |
9,8 |
0,29 |
10,24 |
0,0841 |
8 |
19 |
0,7 |
13,3 |
2,8 |
0,09 |
7,84 |
0,0081 |
9 |
28 |
0,9 |
25,2 |
11,8 |
0,29 |
139,24 |
0,0841 |
10 |
5 |
0,2 |
1 |
-11,2 |
-0,41 |
125,44 |
0,1681 |
Итого: |
162 |
6,1 |
116,5 |
|
|
581,5681 |
0,569 |
В среднем |
16,2 |
0,61 |
11,65 |
|
|
|
0,0569 |
Для изучения зависимости между объемом товарооборота и издержками обращения построить линейное уравнение связи.
Для определения тесноты связи вычислить линейный коэффициент корреляции.
Поясните смысл полученных показателей.
=
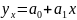
581.5681=
0.61-
0.035*16.2= 0.043
–
уравнение
регрессии
С увеличением товарооборота на 1 млн.тг, то уровень издержек обращения по отношению к товарообороту увеличится на 3,5%
=
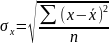=7.626
=
= 0.239
=
= 0.97
Это означает , что в 94,09 случаях уровень издержек увеличится с ростом товарооборота.
21.Имеются данные по распределению рабочих по непрерывному стажу на предприятии:
Непрерывный стаж, лет |
До 2 |
2-4 |
4-6 |
6-8 |
8-10 |
Более 10 |
Число рабочих |
15 |
18 |
35 |
17 |
8 |
7 |
Вычислить: а) средний непрерывный стаж работы; б) среднее квадратическое отклонение; в) коэффициент вариации
РЕШЕНИЕ:
Средний непрерывный стаж работы:
Среднее квадратическое отклонение:
=
=
Kоэффициент вариации
Средний стаж рабочих составляет 5,12 лет. Коэффициент вариации превышает 0,40, это означает , что совокупность является неоднородной.
Имеются данные о производстве молока:
Определите: а) среднее количества молока, моду, медиану, б) среднее квадратическое отклонение; в) коэффициент вариации
Решение:
Произведено молока, кг |
Кол-во коров (f) |
Среднее значение интервала (х) |
X*f |
Сумма накопленных частот, S |
(x-2 |
(x-2 *f |
400-600 |
1 |
500 |
500 |
1 |
944 784 |
944 784 |
600-800 |
7 |
700 |
4900 |
8 |
595 984 |
417 1888 |
800-1000 |
10 |
900 |
9000 |
18 |
327 184 |
327 1840 |
1000-1200 |
13 |
1100 |
14300 |
31 |
138 384 |
1798 992 |
1200-1400 |
15 |
1300 |
19500 |
46 |
29584 |
443 760 |
1400-1600 |
16 |
1500 |
24000 |
62 |
784 |
12 544 |
1600-1800 |
12 |
1700 |
20400 |
74 |
51 984 |
623 808 |
1800-2000 |
10 |
1900 |
19000 |
84 |
183 184 |
183 1840 |
2000-2200 |
8 |
2100 |
16800 |
92 |
394 384 |
3155 072 |
2200-2400 |
6 |
2300 |
13800 |
98 |
685 584 |
4113 504 |
2400-2600 |
2 |
2500 |
5000 |
100 |
1056 784 |
211 3568 |
Всего |
100 |
|
147200 |
|
4408624 |
22481600 |
А) Средняя количества молока определяется по формуле среднеарифметической взвешенной:
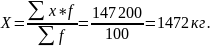
В данном примере модальный интервал находится в пределах группы 1400-1600 , так как на этот интервал приходится наибольшая частота (16).
Рассчитаем величину моды:
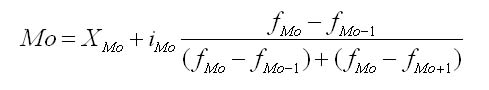=1400+11*((16-15))/(16-15)+(16+12)=1400+0,38=1400,38
Вычислим медиану.
Б) Среднее квадратическое отклонение:
=
= 474,14 кг.
В) Коэффициент вариации:
23. Имеются данные по 10 однородным предприятиям:
Рассчитайте уравнение регрессии зависимости между выпуском бракованной продукции и профессиональной подготовкой рабочих; вычислите коэффициент корреляции. Сделайте выводы.
№ предприятия |
|
|
|
|
|
|
|
|
|
|
Итого |
Среднее |
Кол-во рабочих с профессиональной подготовкой,% |
10 |
12 |
14 |
17 |
24 |
28 |
30 |
35 |
40 |
50 |
260 |
26 |
Кол-во бракованной продукции,% |
18 |
17 |
14 |
12 |
10 |
10 |
8 |
9 |
6 |
6 |
110 |
11 |
x*y |
180 |
204 |
196 |
204 |
240 |
280 |
240 |
315 |
240 |
300 |
2399 |
239,9 |
x-ẍ̅ |
-16 |
-14 |
-12 |
-9 |
-2 |
2 |
4 |
9 |
14 |
24 |
0 |
0 |
y-ӯ |
7 |
6 |
3 |
1 |
-1 |
-1 |
-3 |
-2 |
-5 |
-5 |
0 |
0 |
(x-ẍ̅)² |
256 |
196 |
144 |
81 |
4 |
4 |
16 |
81 |
196 |
576 |
1554 |
155,4 |
(y-ӯ)² |
49 |
36 |
9 |
1 |
1 |
1 |
9 |
4 |
25 |
25 |
160 |
16 |
Решение:
a₁=
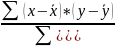= (-16*7-14*6-12*3-9+2-2-12-18-14*5-24*5-112-84-36-9-30-70-120) /
1554= -461/1554=-0,297
a₀ = ӯx - a₁ x =11+0,297*26=18,722=18,72
Y=a₀ + a₁ x= 18,72-0,297х - уравнение регрессии
Это означает, что с увеличением рабочих с профессиональной подготовкой уменьшается количество бракованной продукции на 29,7%. Но это произойдет в том случае, если между двумя данными факторами существует связь, чтобы определить ее наличие и измерить тесноту связи рассчитывают коэффициент корелляции.
σx=
(1554/10)
½=12,77
σy=
=(160/10)
½= 4
= (239,9-26*11) / 12,47*4= -46,1/49,88=-0,92
Наличие связи установлено- обратная сильная. Рассчитанный коэффициент корелляции необходимо проверить на достоверность. Для этого нужно рассчитать критерии надежности:
tr= |r|/σx
r²= 0.846*100%=84,6 - это означает, что в 85 случаях из 100 количество бракованной продукции снижается с ростом рабочих с профессиональной подготовкой.
σ=(1- r²) / n½= (1-84.6)/3.16=-83.6/3.16=-26.46
0.92/-26.46=0.03 коэффициент превысил свою ошибку 0,03 раз, а значит связь между ними можно считать достоверной.
По данным 8 однородных магазинов вычислите коэффициент корреляции, уравнение регрессии. Сделайте выводы:
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Итого |
Среднее |
Товарооборот, млн.тг |
7 |
10 |
15 |
20 |
30 |
45 |
60 |
120 |
307 |
38,4 |
Уровень издержек обращения по отношению к товарообороту,% |
10,0 |
9,0 |
7,5 |
6,0 |
6,3 |
5,8 |
5,4 |
5,0 |
55 |
6,9 |
x*y |
70 |
90 |
112,5 |
120 |
189 |
261 |
324 |
600 |
1766,5 |
220,81 |
x-ẍ̅ |
-31,4 |
-28,4 |
-23,4 |
-18,4 |
-8,4 |
6,6 |
21,6 |
81,6 |
|
|
y-ӯ |
3,1 |
2,1 |
0,6 |
-0,9 |
-0,6 |
-1,1 |
-1,5 |
-1,9 |
|
|
(x-ẍ̅)² |
985,96 |
806,56 |
547,56 |
338,56 |
70,56 |
43,56 |
466,56 |
6658,56 |
9917,48 |
1239,69 |
(y-ӯ)² |
9,61 |
4,41 |
0,36 |
0,81 |
0,36 |
1,21 |
2,25 |
3,61 |
22,62 |
2,83 |
Решение:
Yx=a₀ + a₁ x
a₁= = ((31.4*3.1)+(-28.4*2.1)+(-23.4*0.6)+(-18.4*(-0.9))+(-8.4*(-0.6))+(6.6*(-1.1))+(-1.5*21.6)+(-1.9*81.6)) / 1239.69 = -344.12 / 1239.69 = -0.278
a₀ = ӯx - a₁ x = 6.9 + 0.278*38.4 = 17.58
Y=a₀ + a₁ x = 17.58 + (-0.278)x
Y= 17.58 + (-0.278)x - уравнение регрессии
С увеличением товарооборота на 1 миллион тенге, то уровень издержек обращения по отношению к товарообороту уменьшается на 27.8%.
σx= (9917.48/8)½ = (1239.69)½ = 11.12
σy= = (22.62/8)½ = (2.83)½ = 1.68
= (220.81 – 38.4*6.9) / 11.12*1.68 = -4415/18.6816=-2.4
=
(-2.4)²= 5.76*100=576
Это означает, что в 576 случаях уровень издержек снизился с ростом товарооборота.