8.2.1 Үш еселі интегралды есептеу

1) Үш еселі интегралды қабырғалары координат жазықтықтарына параллель болатын параллелпипед бойынша есептеу. Параллелепипед болса, онда

.

2) Үш еселі интегралды қисық сызықты аймақ бойынша есептеу. Интегралдау аймағы D мына теңсіздіктермен , анықталса, мұндағы сегментінде бірмәнді, үзіліссіз функциялар, демек

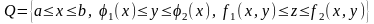
болса, онда

.

Мысал 1 Үш еселі интегралды берілген аймақ бойынша есептеу керек.

(8-сурет).

Шешуі z

2

0 y

х

8-сурет

8.2.2 Үш еселі интегралда айнымалыларды ауыстыру

Кеңістіктегі қисық сызықты координаттар. Координаттары 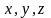болатын үш өлшемді кеңістікте құрама-сыптығыр L бетімен шенелген V аймағы және координаттары болатын үш өлшемді кеңістікте N құрама-сыптығыр бетімен шенелген V^/ аймағы берілсін (9-сурет).

Z W

N

L

0 Y 0 V

X U

9-сурет

V мен V^/ аймақтары нүктелерінің арасында бір мәнді және үзіліссіз сәйкестік бар болсын. Сонымен бірге тура сәйкестік

(8.10)

формулаларымен анықталып, кері сәйкестік

(8.11)

формуларымен анықталсын. (8.10) және (8.11) функцияларының өздері де, бірінші ретті дербес туындылары да үзіліссіз деп жориық. Сонда үзіліссіз якобиандар

мен

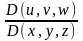
бар болады.

Теорема Егер функциясы тұйық, шенелген V аймағында үзіліссіз, (8.11) функциялары V аймағын V^/ аймағына өзара бір мәнді бейнелейтін, үзіліссіз дифференциалданатын және якобианы нөлге тең емес түрлендірулер болса, онда үш еселі интегралда айнымалыларды ауыстыру мына формула арқылы орындалады:

мұндағы

J – (8.10) функциялардың якобианы деп аталады.

2) Кеңістіктегі цилиндрлік координаттар. Декарттық координаттар жүйесінде 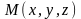нүктесі беріліп, оның Оху жазықтығындағы проекциясы М₁ нүктесі болсын. М нүктесі оның аппликатасы z және М₁ өзінің полярлық кординаттары мен арқылы анықталса, онда шамалары М нүктесінің цилиндрлік координаттары болады. М нүктесінің декарттық және цилиндрлік координаттарының арасындағы байланыс мына формулалармен анықталады (10-сурет):

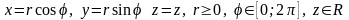
10-сурет

координаттарын координаталарымен ауыстыру якобианы:

болады. Сондықтан үш еселі интегралда айнымалыларды ауыстыру мына формула арқылы орындалады:

.

3) Сфералық координаттар. Оxyz кеңістігінде М нүктесінің орнын:

а) О нүктесінен М нүктесіне дейінгі қашықтық ;

б) ОМ кесіндісі мен Оz өсінің оң бағыты арасындағы бұрыш ;

в) ОМ кесіндінің Оху жазықтығындағы проекциясы ОМ₁ мен Ох өсінің оң бағыты арасындағы бұрыш арқылы анықтасақ, онда осы шамалары М нүктесінің сфералық координаттары болады. М нүктесінің декарттық және сфералық координаттар арасындағы байланыс мына формулар арқылы анықталады (суретке қара):

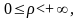
z

 M



 у y

х M₁

x

11-сурет

Декарттық координаттарды сфералық координаттарға ауыстыру якобианы былайша анықталады:

.

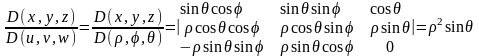Мысал 2 интегралды есептеу керек, егер интегралдау аймағы болса, демек беті және жазықтығымен шенелген дене бойынша.

Шешуі Интегралды цилиндрлік кординаттарға көшу арқылы есептейміз:

Цилиндрлік координаттар жүйесінде интегралдау аймағы мына теңсіздіктер арқылы анықталады: . Сондықтан,

Мысал 3 Интегралдау аймағы , демек радиусы 1-ге тең, центрі координат басында жатқан шар.

Шешуі Интегралды сфералық координаттарға көшу арқылы есептейміз:

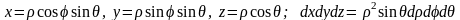
Сфералық координаттар жүйесіндегі V-ның бейнесі:

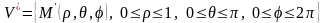
Сондықтан,

болады.