8 Екі және үш еселі интегралдар
8.1 Екі еселі интегралдың анықтамасы және оның негізгі қасиеттері
Бізге
Оху жазықтығының тұйық D аймағында оң
таңбалы, үзіліссіз
функциясы берілген.
Есеп:
Жасаушылары Оху жазықтығына перпендикуляр
жоғарғы жағынан
бетімен, төменгі жағынан D аймағымен
шенелген цилиндрлік дененің көлемін
табу керек. Бұл денені цилиндроид деп
атайды. Мұның көлемін табу үшін, оның
табаны D –ны
бөліктерге бөлшектеп, әрқайсысынан бір
нүкте
таңдайық. Сонда жуық шамамен
цилиндрдің і – ші бөлігінің көлемін
береді (5-сурет).
5-сурет
Демек
интегралдық қосынды, жуық шамамен бүтін
цилиндрдің көлемі. Егер
,
қосынды Vn
шегін табатын болсақ, онда цилиндроидтың
көлемі шығады.
(8.1)
Осы шекті D аймағы бойынша функциясынан алынған екі еселі интеграл деп атайды.
Екі еселі интегралдың негізгі қасиеттері:
1)
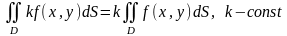
2)
3) Егер D=D1D2 D=D1D2 болса, онда
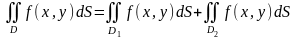
4)
Егер D аймағы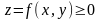нда,
,
онда
5)
Егер D аймағында,
теңсіздігі орындалса, онда
8.1.1 Екі еселі интегралды есептеу
Интегралдау
аймағы D мына сызықтармен
шенелген болсын. Мұндағы
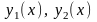
сегментінде бірмәнді, үзіліссіз
функциялар. Осы шарттар орындалған
жағдайда:
(8.2)
Бұл
формуланың оң жағындағы интегралды
қайталама
интеграл деп атайды. Егер D аймағы
,
сызықтармен шенелген болса, онда
(8.3)
Бұл интегралдардың біреуін екіншісімен ауыстыруға болады.
Мысал 1 Интегралдау ретін өзгертіңіз.
Шешуі
D аймағы
,
осыдан
.
Мысал 2 Интегралдау ретін өзгертіңіз.
Шешуі D=D1+D2 болғандықтан (6-сурет),
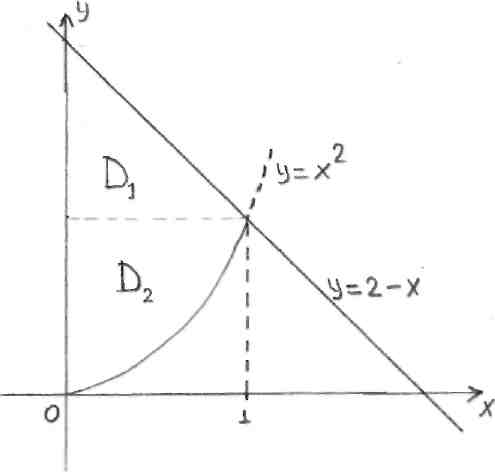
6-сурет
8.1.2 Екі еселі интегралда айнымалыларды ауыстыру
Екі
еселі интеграл
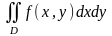қарастырайық.
функциясы шенелген тұйық D аймағында
үзіліссіз.
(8.4)
формулалары
арқылы жаңа
және
аргументтеріне көшіп (8.4) теңдеулер
жүйесінен
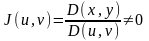деп есептеп,
(8.5)
функциялары
анықталады.
нүктесіне
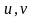координаттар жазықтығында
нүктесі сәйкес келеді. Онда (8.4)
формуласындағы функциялардың дербес
туындылары бар болады да, мына анықтауыш
,
сонда
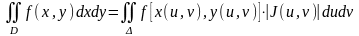(8.6)
теңдігі
орындалады.
-ны
функцияларының Якобинаны деп атайды.
– (8.4) түрлендіруіндегі D-ның бейнесі.
Егер (8.4) формуладан полярлық координаталарға көшетін болсақ, яғни
(8.7)
деп алсақ, онда, (8.7) алмастыруының Якобианы
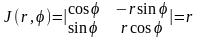
екенін ескеріп,
(8.8)
теңдігіне келеміз.
Мысал
3
,
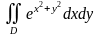D - бірінші квадрантта жататын
дөңгелегінің бөлігі
.
Осы интегралды есептеу керек.
Шешуі
формулаларынан
;
.
Сондықтан,
.
Мысал
4
интегралын есепте, егер D:
түзулерімен шенелген аймақ болса.
Шешуі
Айталық,
болсын, онда
,
.
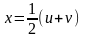Ал түрлендіру Якобианы
.
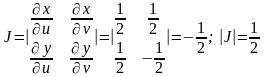Сондықтан,
,
.
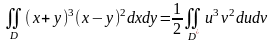
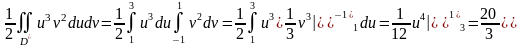