1.Логика алгебрасының функцияларына анықтама беріп негізгі функцияларына мысал келтір.Логика алгебрасының функциясы (АЛФ) деп– екілік ауысуды ( , , ... ) жинақтау кезінде анықталатын және өздерінің мәні ретінде нөл немесе бірді өздері қабылдау кезінде анықталатын функцияарды атайды. Логика алгебрасының функциясын беру – оның мәнін (0 немесе 1) аргумент мәндерінің әрбір мүмкін болатын жинағында анықтау болып табылады. Аргументтеррдің әр түрлі жинақтарының мөлшері n разрядтың көмегімен, яғни 2, суреттелетін әр түрлі сандардың мөлшеріне тең. АЛФ аргументтерін әрбір жинақтауда екі мәннің біреуі ғана қабылдана алады, сол n аргументтегі әр түрлі АЛФ мөлшері -не тең болады. Төменде n=0, 1, 2 үшін n аргументтегі АЛФ-ның барлық мүмкіндіктері қарастырылған.

1. n=0. =2-тең әр түрлі АЛФ қолданылады; f1=0 – нөл тұрақты, f2= - бір тұрақты.

2. n=1. =4 тең әр түрлі АЛФ қолданылады.

Оларды сол жақ бөлігінде аргументтердің мүмкін болатын жинағы көрсетілген, ал оң жақ бөлігінде АЛФ әр жинақта болатын 2.1- кестеден анықтауға болады. f1 және f2 белгілі, онымен қоса екі АЛФ анықталған: f3=x- теңдік функциясы; f4= - теріске шығару функциясы ( f x-ке тең емес деп оқылады).

1-кесте

Х	f1	f2	f3	f4
0 1	0 0	1 1	0 1	1 0

3. n=2. =16 тең әр түрлі АЛФ қолданылады, олар ақиқат кестесінде қолданылады(2.7-кесте). Алғашқы 6 АЛФ 2.2-кестеде белгілі: f1-0 константа; f2-1 константа; f3= ; f4= ; f5= ; f6= . f₇ функциясы дизъюнкция деп аталып, f₇= \/ немесе f₇= + деп белгіленеді; егер ең болмағанда аргументтердің біреуі бірге тең болған кезде дизъюнкция 1 мәнін қабылдайды.

Таблица 2.

X1	x2	f1	f2	f3	f4	f5	f6	f7	f8	f9	f10	f11	f12	f13	f14	f15	f16
0 0 1 1	0 1 0 1	0 0 0 0	1 1 1 1	0 0 1 1	0 1 0 1	1 1 0 0	1 0 1 0	0 1 1 1	0 0 0 1	1 0 0 1	0 1 1 0	1 1 0 1	1 0 1 1	1 0 0 0	1 1 1 0	0 0 1 0	0 1 0 0

f8функциясы конъюнкция деп аталады, f8= /\ деп белгіленеді; егер екі аргумент те 1-ге тең болса, конъюнкция 1мәнін қабылдайды. f9функциясы эквивалентті деп аталады және f9= ~ деп белгіленеді; егер екі аргумент тең болса 1мәнін қабылдайды. f10 функциясы екі модуль бойынша қосылу деп аталады және f10=  деп белгіленеді; аргумент мәндері бір-біріне сәйкес келмейтін жинақта 1мәнін қабылдайды. f11 функиясы x1-дің x2-дегі импликациясы деп атайды және f11=  деп белгіленеді. f12 функциясы x2-нің x1-дегі импликациясыдеп аталады және f12=  арқылы белгіленеді. f13 функциясы Вебба функциясы деп аталады және f13=  деп белгіленеді.f14 функциясы Шеффер функциясы деп аталады және f14= / деп белгіленеді. f15жәнеf16 функцияларының арнайы атаулары болмайды.

Жоғарыда айтылған 14 АЛФ қарапайым деп атайды және олардың логика алгебрасында алар орны ерекше.

2.Санақ жүйелеріне анықтау беріп негізгі түрлеріне мысалдар келтір. Санау жүйесі. Санау жүйесі сандарды цифрлық таңбалармен жазуға арналған әдістер мен ережелер жинағы болып табылады. Барлық санау жүйелері позициялық және позициялық емес болып бөлінеді. Сандар цифрларының салмақтары әртүрлі және де салмақ мәні цифр позициясының номеріне тәуелді болатын санау жүйелерін позициялы деп атаймыз. Позициялық жүйеге ең қарапайым мысал ретінде ондық жүйені алуға болады. Сандар разрядтарының салмақтары олардың позициясына тәуелді болмайтын санау жүйесін позициялық емес деп атаймыз. Екілік санау жүйесінің негізі: , ол екілік санау жүйесінде 10₍₂₎ түрінде жазылады. Бұл жүйенің базисі тек екі цифрдан тұратыны белгілі: 0 және 1. Екілік санау жүйесінде арифметикалық әрекеттерді орындау төмендегі ережелерге негізделуі тиіс.

Екілік қосу	Екілік азайту	Екілік көбейту
0+0=0 0+1=1 1+0=1 1+1=10	0-0=0 1-0=1 1-1=0 10-1=1	0*0=0 0*1=0 1*0=0 1*1=1

Сегіздік санау жүйесінің негізі «сегіз» саны болып табылады, ол 10₍₈₎ түрінде жазылады да, келесі сегіз цифрдан тұрады: 0, 1, 2, 3, 4, 5, 6, 7. Он алтылық санау үйесіндегі «он алты» негізі 10₍₁₆₎ түрінде жазылады және де 0 ÷ 15 аралығындағы цифрлардан тұрады. Оларды 0 ÷ . 9 белгілеу үшін ондық санай жүйесіне сәйкес келетін символдар қолданылады, ал 10, 11, 12, 13,14, 15 мәндері үшін A, B, C, D, E, F латын алфаваитінің әріптері қолданылады.

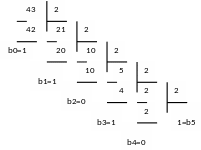
Мысал 2.3. А=43 ондық санын екілік сан( =2).у жүйесіне ауыстыру.

Шешімі:

Жауабы: А(2)=101011(2).

3. Оң және теріс сандарды кодалау қағидасын түсіндіріп жаз. Жалпы алғанда саны ЭЕМ-де 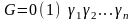түрінде бейнеленеді, жоғарыда айтқандай, мұнда 0 немесе 1 –сан таңбасы, сондай ақ, 0 - (+), 1 - (-), ал - дегеніміз 0 ÷ (р-1) диапазонындағы цифрлар.

Сандарды өңдеуді қолайлы ету мақсатында (процессор тек қосу амалын орындай алатынын ескере отырып) тура, кері және қосымша кодалар деген түсінік енгізіледі.

Мысалы, 5₍₁₀₎ саны келесі түрде жазылады:

Тура кода – 0.101₍₂₎;

Кері кода – 1.010₍₂₎;

Қосымша кода – 1.011₍₂₎.

4.Сандарды жылжымалы үтір формасында белгілеудің қағидаларын сиппаттап мысал келтір. мантисса және деңгей көрсеткіші ретінде сақталатын нақты сандардың көрініс формасы.Бұл ретте жылжымалы үтірлі санда тұрақты қатысты нақтылық пен айнымалы абсолют бар.

Жылжымалы үтірлі санның құрамы:-мантисса белгісі(санның оң немесе терістігіне нұсқайды),-мантиссалар(тәртіпті ескермей санның мағынасын білдіреді ),-тәртіп белгісі,-тәртіп(мантисса көбейтілетін санның негізінің деңгейін білдіреді)

Қалыпты форма және Қалыптандырылған(нормализованная) форма. Жылжымалы үтірлі санның қалыпты форма(нормальная форма) .Бұл кезде мантисса [0; 1) ( ) интервалында орналасады. Қалыпты күйде болмайтын болса, қалыптыға қарағанда нақтылығын жоғалтады. Форманың мұндай түрінің кемшілігі:кейбір сандар біркелкі жазылмайды(мысалыға 0,0001 төрт түрде жазуға болады- 0,0001·10⁰, 0,001·10⁻¹, 0,01·10⁻², 0,1·10⁻³), сондықтан жазбаның басқа түрі –ондық мантисса 1-ден 10ға дейінгі мәнді қабылдайтын , немесе екілік мантисса 1-ден-2-ге дейінгі мәнді қабылдайтын қалыптандырылған форма кең таралған. Бұл формада кез келген сан жалғыз бейнеде жазылады.Кемшілігі : бұл күйде 0-ді көрсете алмаймыз, сондықтан 0 саны үшін арнайы бит қарастырылады. Калыптандырылған күйде екілік санды мантиссаның жоғарға разряды «1»-ге тең. Сандарды жылжымалы үтірлі формасында жазу –разрядтың тұрақты санын және нақтылығын келістіру арқылы үлкен диапозонды есептеулерді жүргізуге мүмкіндік береді.Мысалы, ондық жүйеде: көбейту кестесі 0,12 × 0,12 = 0,0144

Қалыпты формада: (1,20·10⁻¹) × (1,20·10⁻¹) = (1,44·10⁻²)

Тұрақты үтір формасында: 0,120 × 0,120 = 0,014.

5.Сандарды тұрақты үтір формасында белгілеудің қағидаларын сипаттап мысал келтір. Берілген бөлінгіш пен бөлгіштің қатынасы арқылы C=A/B-меншіктісі(частное) анықталады. Сан нөлге бөлінбегендіктен, В0 болуы анық жағдай. Тұрақты үтірлі цифрлық машинасында бірден кіші болатын [Х]<1 күйі жиі қолданылатын болғандықтан, бөлінгіш, бөлгіш және меншіктіге қосымша шектеулер еңгізіледі: А<1, В<1, С<1. Соңғы теңсіздектен, А<Вболуы тиіс.

Егер бөлінгіштің бөлгішке қатынасының мәні 1–ден үлкен болатын болса, онда операция орындалмайды. Бұдан "Асыра толтыру" немесе "Қате" сигналы шығады. Операцияда тура кодтауда сандарды бөлгенде бөлінгіш пен бөлгіштің модульдері қатысады. Меншіктінің белгісі (көбейтудегі сияқты) екі бөлінгіш пен бөлгіш модульдерінің қосындысымен анықталады,.

Бөлу процесі бөлгіштің басында бөліндіден шегергендегі тізбектемелі операциялардан және әр бөлген кездегі солға қарай бір разряд жылжу уақытында пайда болған қалдықтардан тұрады. Егер қалдық оң болса, онда меншіктінің разрядына 1 жазылады; егер теріс болса, 0 жазылады. Шегеру процесі қайталана береді, қайталау саны меншіктінің рязрядтылығына байланысты анықталады.

Меншіктінің келесі разрядтылығын анықтауда кезекті теріс қалдықды алғаннан кейінгі жүргізілетін жұмыстарға байланысты қалдықтарды қалпына келтіретін және қалпына келтірілмейтін тәсілдерін бөліп көрсетеді.

Бірінші тәсілде алғашқы қалдық Убөлгіштің   теріс қалдықпен қосындысы арқылы анықталады( +У). Меншіктінің келесі разрядтылығын алу үшін қалпына келтірілген қалдық бір разрядқа солға жылжиды және одан бөлгіш алынады : 2·( +У)-У.

Екінші тәсілде теріс қалдық бір разряд солға жылжиды және оған бөлгіш қосылады : 2 +У, т.к. 2( +У)-У=2 +У.

Бірінші вариантты іске асыру үшін 2n – оңға жылжитын бөлгіштің разрядты регистры және 2n - разрядты сумматоры, солға жылжитын меншіктінің (n+1) – разрядты регистры және басқару схемасы керек.

Екінші вариантты іске асыру үшін n – бөлгіштің разрядты регистры, (n+1) солға жылжитын меншіктінің разрядты регистры, n – солға жылжитын разрядты сумматор және басқару схемасы.

Мысал Х = 5 X_{доп мод} = 00.101₂

+ +

Y = -7 Y_{доп мод} = 11.001₂

__________ ____________

Z = -2 Z_{доп мод} = 11.110₂

6. Комбинациялық схемалардың анықтамасын беріп, олардың түрлерін атап жаз. Цифлық логикалық құрылғылардың функционалдық түйіндері екіге бөлінеді: комбинациялық және тізбектелген. Комбинациялық типті функционалдық түйіндер деп шығыс сигналдары кез келген уақыттың дискретті мезетінде дәл осы кезде кірісте тұрған бірмәнді түрде логикалық сигналдармен анықталатын логикалық құрылғылар.

Цифрлық құрылғылардың тізбектелген функционалдық түйіндер құрамында міндетті жады элементтері болады. Сондықтан бұл құрылғылар жадысы бар автоматтар немесе цифрлық автоматтар (ЦА) деп аталады.

Комбинациялық құрылғылар арасында іс жүзінде кеңінен қолданылатындары типтік функционалдық түйінде: шифраторлар, дешифраторлар, мультиплексорлар, демультиплексорлар, компараторлар, кода түрлендіргіштер, бақылау схемалары, сумматорлар және т.б.

Шифраторлар. Шифратор деп сандарды ондық санау жүйесінен екілік санау жүйесіне түрлендіретін комбинациялық құрылығыны айтамыз. Шифратор кірісіне тізбекті түрде ондық сандар мәндері меншіктеледі. Шифратор кірістерінің біріне активті логикалық сигнал берген кезде, оның шығысында белсенділенген кіріске (яғни ондық санға) сәйкес екілік кода қалыптасады. 2ⁿ кірісі және n шығысы бар шифратор толық шифратор деп аталады. Егер кіріс саны 2ⁿ-ден кем болса, ол толық емес шифратор деп аталады.

1-сур. Шифратордың шартты-графикалық белгіленуі (а) және оның логикалық схемасы (ә).

Дешифраторлар. Дешифратор немесе декодер деп кірістегі n-разрядты екілік коданы шығыста “m-нан1” түріндегі кодаға түрлендіретін комбинациялық типті функционалды түйін, мұнда n және m – мүмкін болатын m шығыс сигналдарының бірі. Басқаша айтқанда кіріс сигналдарының әр бір нақты комбинациясы үшін сәйкес шығыс сигналдары мысалы логикалық «1»-ге тең нақты бір мәнді қабылдайды, ал қалғандары логикалық «0» мәнін қабылдайды. Егер дешифратордың n кірістері оның m шығыстарымен m = 2ⁿ қатынасы арқылы байланысқан болса, онда дешифратор толық деп саналады. Егер m < 2ⁿ болса, яғни дешифратор шығысында кіріс сигналдарының барлық мүмкін болатын комбинациясы іске асырылмаса – толық емес деп аталады. Мысалы, толық емес дешифратор деп екілік коданы екілік-ондық кодаға түрлендіретін 4 кірісі бар және 10 шығысы бар дешифратор аталады.

2-сур. Инверсті шығысы бар дешифратор схемасы (а) және оның шартты графикалық белгіленуі (ә).

Мультиплексор. Мультиплексор деп ақпаратты бірнеше кіріс каналынан бір шығысқа тасымалдауды басқаратын құрылғы.

3-сур. Мультиплексор схемасы (а) және оның шартты-графикалық белгіленуі (ә)

Демультиплексор бір ақпараттық кірістен келгкен ақпаратты адрестік кірістердегі сигналға байланысты бірнеше шығыстардың біреуіне тасымалдауды басқаруға арналған комбинациялық логикалық құрылғы.

4-сур. Демультиплексор схемасы (а) және оның шартты-графикалық бейнеленуі.

Цифрлық компараторлар. Цифрлық компараторлар екілік кодада берілген сандарды екі санды салыстыру жұмысын атқарады. Компаратор кірістерінің саны салыстырылатын a және b сандарының екілік кодаларының разрядтылығымен анықталады.

5-сур. Бір разрядты компаратордың схемасы.

7. Шектелген автоматтарға анықтама беріп олардың түрлерін атап жаз. Көптеген жағдайларында t_i моментінде құрылғы жұмысы t_i уақыт моментінде берілген кіріс сөз ғана аударылып қоймайды, бірақ сонымен қатар алдағы өткен уақыт моментіне түскен кіріс сөздерге тәуелді болады. Бұл жағдайда жиі, жай ғана шектелган автомат деп аталатын жадысы бар автоматпен жұмысы болады. Шектелген автоматтар автоматтар теориясының кибернетика бөлімінде оқылады.

Дискретті ақпаратты түрлендіру үшін қызмет ететін құрылғы дискретті автомат деп аталады. Дискретті ақпарат әріптер сандармен сәйкес келетін алфавитпен беріледі. Сондықтан дискретті автоматтарды сандық деп те атау қабылданған.

Синхронды автоматтардың автоматтың күйін өзгерту мүмкін болатын уақыт моментінде арнайы құрылғы – синхроимпульстер генераторы анықталады. Асинхронды автоматтарда бір күйден екінші күйге ауысу моменттері алдын ала анықталмайды және бірдей емес уақыт аралығы арқылы жүзеге асады. Осы себептен асинхронды автоматтар теориясы синхронды автоматтар теориясынан ерекшеленеді.

Автоматтардың жалпы теориясы автоматтардың абстракты және құрылымды теорияларына бөлінеді. Автоматта алфавиттер бар: Х – кіріс, У – шығыси және А – жағдайы. Кіріс сигналдардың саны шектеулі, және олар бір күден екіншіге ауысу себебі ретінде қарастырылады: a(t-1)a(t), где аА. Шығыс сигналдардың саны шектеулі және әрбір өзгеше автомат уақытының О моментіне t моментінде пайда болуы мүмкін y(t) шығыс сигналына сәйкес келеді, бірақ осы уақыт моментіне (уУ и хХ) сәйкес келетін x(t) кіріс сигналынан кейін. У(t) a(t-1) күйінен a(t)-ға ауысу моментінде немесе ауысудан кейін пайда болуы мүмкін. Бірінші жағдайда y(t) x(t) және a(t-1) жұбымен бір мағыналы анықталады. Сондықтан автоматтар I түрдегі (Мил автоматы) II түрдегі (Мур автоматы) болып бөлінеді.

Абстрактылы автомат алты объектінің жиынтығы ретінде көрсетіледі: кіріс сигналдардың Х шекті жиынтығы (кіріс алфавит); шығыс сигналдардың У шекті жиынтығы(шығыс алфавит); автомат күйлерінің жиынтығы деп аталатын А жиынтығы, А және У жиынтығындағы а,х(аА и xX) жұбының жиынтығының бірмағыналы кескінін беретін (а, х) и (а, х) функциясы және автоматтың бастапқы күйі деп аталатын А жиынтығынан. (а, х) функциясы автоматтың ауысу функциясы, ал (а, х) функциясы шығыстар функциясы немесе жылжыған шығыстар функциясы деп аталады. Егер автомат шығыстар функциясымен көрсетілсе, онда бұл автомат I түрдегі(Мил), жылжыған шығыстар функцичсы – II турдегі(Мур).

Мил автоматы үшін: a(t)=(a(t-1)), х(t); У(1)=(а(t-1)), х(t); (t= ).

Мур автоматы үшін: a(t)=(a(t-1)), х(t); У(1)=(а(t)), х(t)= (а(t)); (t= ).

Автомат берудің бірнеше әдістері бар. Көп таралғандары кестелік және графикалық болып табылады. Кестелік әдісте автоматтарды беру автомат жұмысына сипаттама ауысудың және шығыстың кестесі беріледі. 1-кестеде ауысу функциясы а=(а, х) берілген , ал 2-кестеде Мил автоматының шығыс функциясы y=(а, х) берілген.

1-кесте 2-кесте

Автоматтарды көрсету графикалық әдісте автоматтың жұмыс сипаттамасы төбелері автоматтың күйіне сәйкес келетін бағытталған байланыс графигі түрінде беріледі, доғалары – олардың арасындағы ауысумен. Графтың екі а_i және а_s төбесі егер автоматта а_i-ден а_s-ке ауысу болатын болса,яғни а_s=(а_i, x_j) кейбір жағдайда x_jX, а_i-ден а_s-ке бағытталған доғалар өзара автоматты байланыстырылған. Мил автоматы графының (a_i, а_s) доғасына x_j кіріс сигналы және y_g=(a_i, x_j) шығыс сигналы қосымша жазылады, егер ол анықталған болса, басқаша жағдайда сызық қойылады. Мур автоматының графы Мил автоматының графынан граф төбесінде жазылған шығыс сигналымен ерекшеленеді(1-сур.)

1-сур. Автоматтың графикалық бейнеленуі

8. Дешифрратордың элементарлы функциялардан құрылған сұлбасын сызып ақиқат кестесін көрсет.

Дешифратор немесе декодер деп кірістегі n-разрядты екілік коданы шығыста “m-нан1” түріндегі кодаға түрлендіретін комбинациялық типті функционалды түйін, мұнда n және m – мүмкін болатын m шығыс сигналдарының бірі. Басқаша айтқанда кіріс сигналдарының әр бір нақты комбинациясы үшін сәйкес шығыс сигналдары мысалы логикалық «1»-ге тең нақты бір мәнді қабылдайды, ал қалғандары логикалық «0» мәнін қабылдайды. Егер дешифратордың n кірістері оның m шығыстарымен m = 2ⁿ қатынасы арқылы байланысқан болса, онда дешифратор толық деп саналады. Егер m < 2ⁿ болса, яғни дешифратор шығысында кіріс сигналдарының барлық мүмкін болатын комбинациясы іске асырылмаса – толық емес деп аталады. Мысалы, толық емес дешифратор деп екілік коданы екілік-ондық кодаға түрлендіретін 4 кірісі бар және 10 шығысы бар дешифратор аталады. Дешифратор жұмысы шифратордың ақиқаттық кестесіне сәйкес ақиқаттық кестемен баяндалады, мұнда тек кіріс және шығыс сигналдарының орындары ауысқан.

Входы				Выходы
8	4	2	1	0	1	2	3	4	5	6	7	8	9
0	0	0	0	1	0	0	0	0	0	0	0	0	0
0	0	0	1	0	1	0	0	0	0	0	0	0	0
0	0	1	0	0	0	1	0	0	0	0	0	0	0
0	0	1	1	0	0	0	1	0	0	0	0	0	0
0	1	0	0	0	0	0	0	1	0	0	0	0	0
0	1	0	1	0	0	0	0	0	1	0	0	0	0
0	1	1	0	0	0	0	0	0	0	1	0	0	0
0	1	1	1	0	0	0	0	0	0	0	1	0	0
1	0	0	0	0	0	0	0	0	0	0	0	1	0
1	0	0	1	0	0	0	0	0	0	0	0	0	1

дешифратордың ақиқат кестесі

Схемотехникалық тұрғыда дешифраторлар ЖӘНЕ (И) немесе ЖӘНЕ-ЕМЕС (И-НЕ) логикалық элементтерінде (ЛЭ) іске асырылады. Соңғы жағдайда дешифратор инверсті шығысы бар дешифратор деп аталады.

Сызықты деп аталатын дешифратордың ең қарапайым схемасында әрбір шығыс функциясын іске асыру үшін жеке n-кірісті ЖӘНЕ немесе ЖӘНЕ-ЕМЕС логикалық элементтері қолданылады. ЖӘНЕ (немесе ЖӘНЕ-ЕМЕС) логикалық элементтері кірістеріне кіріс сигналдарының сәйкес комбинациялары беріледі. ЖӘНЕ-ЕМЕС логикалық элементінен тұратын сызықтық дешифратор схемасы және оның шартты-гарфикалық белгіленуі 2-суретте көрсетілген.

1-суреттегі дешифратор схемасында дешифратор кірісіне келіп түсетін бірфазалы (тура) сигналдардан парафазалы сигналдарды алу үшін қосымша ЖӘНЕ-ЕМЕС элементтері қолданылады. Әрбір ЖӘНЕ-ЕМЕС логикалық элементтердің шығысында m шығыс функцияларының біреуі инверсияланады. Шартты белгінің негізгі бетінде (1.ә-сурет) DC әріптері қойылған, бұл Decoder дегенді білдіреді. дешифратор кірістері олардың екілік салмақтарымен белгіленеді.

Дешифратор микросхемаларында әдетте стробтаушы кірістер орнатылған, оларды белсенді логикалық сигналдың орнауы жұмыс істеуге рұқсатты білдіреді. Егер 1.а-суреттегі дешифратор схемасында Е стробаушы кірісне логикалық 1 сигналы берілсе, дешифратордың шығыс функциялары оның кіріс сигналдарына тәуелді болмайды және оларджың бәрі логикалық 1 мәнін қабылдайды; қарсы жағдайда стробаушы сигнал E=0 дешифратор әдеттегі режимде жұмыс істейді. Мысалы, егер барлық кірістерде логикалық 0 болса, онда шығыста – логикалық 0, ал басқа шығыстарда логикалық 1 болады. Егер x2 кірісінде – логикалық 1 болса, ал басқаларында логикалық 0 болса, онда шығысында - логикалық 0, ал қалғандарында логикалық 1 және т.с.с.

а)

ә)

Сурет –1. Инверсті шығысы бар дешифратор схемасы (а) және оның шартты графикалық белгіленуі (ә).

Цифрлық құрылғыларда дешифраторлар кеңінен қолданылады. Олар кез келген комбинациялық құрылғыларды: мультиплексорларды, демультиплексорларды, кода түрлендіргіштерінде және т.б. жасауда қолданылады. Жадыда сақтау құрылғыларында дешифратор көмегімен ақпаратты жазу және оқу ұяшықтарын таңдайды. Енгізу/шығару құрылғыларында дешифраторлар деректерді тасымалдайтын немесе қабылдайтын көптеген порттардың біреуін таңдауға мүмкіндік береді.

9.Мультиплексордың элементарлы функциялардан құралған сұлбасын сызып ақиқат кестесін көрсет. Мультиплексор деп ақпаратты бірнеше кіріс каналынан бір шығысқа тасымалдауды басқаратын құрылғы. Мультиплексорда ақпараттық кіріспен қоса, адрестік (басқарушы) кіріс және мультиплекор жұмысына рұқсат беруші стробтаушы кіріс бар. Адрестік кірістегі сигналдар дәл қазір ақпараттық кірістердің қайсысы шығыспен қосылғанын анықтайды.

1.сурет.Мультиплексор схемасы

2.сурет.шартты-графикалық белгіленуі

1суретте схемада екі кірісті ЖӘНЕ-ЕМЕС логикалық элементі дешифратордың шығыс сигналдарымен басқарылады, ал дешифратордың кірісіне адрестік сигналдар берілген болатын. Сонымен, дешифратор көмегімен екі кірісті ЖӘНЕ-ЕМЕС логикалық элементтерінің бірі таңдалынады, және сол арқылы және екінші сатыдағы ЕМЕС логикалық элементі арқылы ақпарат шығысқа беріледі. Және бұл жағдайда мультиплексор жылдамдығы дешифратордағы және екі ЖӘНЕ-ЕМЕС логикалық элементтердегі сигналдардың таралуының бөгелу қосындысымен анықталады.

2суретте Е жұмысқа рұқсат беруші кіріс сонымен қатар мультиплексордың функционалдық мүмкіншіліктерін кеңейту үшін қолданылады, мысалы, мультиплексордың ақпараттық кірістерін көбейту үшін (кіріс сөздерінің разрядтылығы өсіру) және мультиплексордың жұмысын басқа құрылғылардың жұмыстарымен синхрондау үшін. 5.1-суретте төрткірісті мультиплексор негізінде құралған 16 ақпараттық кірісі бар мультиплексордың (мультиплексорлық бұтақтың) разрядтылығын өсіру схемасы келтірілген.

Ақиқат кестесі