9 Дәріс. Үзіліссіз кездейсоқ шамалар және олрадың сипаттамалары.

1. Кездейсоқ шаманың үлестіру функциясы және үлестіру тығыздығы

2. Үлестіру функциясының қасиеттері

3. Ықтималдықтар үлестіруінің тығыздығы

Кездейсоқ шаманың үлестіру функциясы және үлестіру тығыздығы

Кездейсоқ шамаларды қарастырғанымызда дискретті және үздіксіз шамалардың болатынын айттық. Дискретті кездейсоқ шаманы оның барлық мәніне сәйкес ықтималдықтарымен берілген таблица арқылы көрсеттік, ал мұндай таблицаны үздіксіз кездейсоқ шама үшін құра алмаймыз. Сондықтан осыған байланысты үздіксіз кездейсоқ шамалар үлестіруін сипаттайтын заңды іздестіруге тура келеді. Әрине әрі дискретті, әрі үздіксіз кездейсоқ шамаларды сипаттайтын кейбір универсал үлестіру заңын табу қолайлы болар еді.

Кездейсоқ шама үздіксіз болғанда мәндеріндегі оқиғалар ұғымын пайдаланбайды, мұның орнына теңсіздігін алады. Мұндағы х-айнымалы шама. Бұл теңсіздікті, кездейсоқ шама х-тен кіші болатын барлық мүмкін мәндерді қабылдайды деп аталады, яғни . Сөйтіп, оның ықтималдығын түрінде жазады. Сондықтан бұл ықтималдық х-тің кейбір функциясы болады, оны деп белгілесек, онда немесе

(1)

болады. Бұл функцияны үлестіру функциясы немесе үлестірудің интегралдық функциясы деп атаймыз.

Х дискретті кездейсоқ шама болса, онда ол шекті немесе санамалы шексіз мәнді қабылдайды және оның әрбір мәніндегі ықтималдық болады. Сондықтан

Үлестіру функциясының қасиеттері

1. х-тің әрбір мәнінде болады.

Д/уі: дейік. Ал болғандықтан, болады.

2. Кездейсоқ шама Х-тің үлестіру функциясы аргументтің теріс емес, кемімейтін функциясы болады, яғни болғанда, болады.

Д/уі: болса, . Мұнда және оқиғалары үйлесімсіз. Олай болса,

.

Бұдан

Демек, .

3. аралығындағы мәндерді қабылдайтын кездейсоқ шама Х-тің ықтималдығы осы интервалдағы функциясының өсімшесіне тең, яғни

.

4. функциясы аралығының кез келген нүктесінде сол жағынан үздіксіз, яғни

.

5. Егер Х кездейсоқ шамасы аралығындағы барлық мәндерді қабылдаса, онда х-тің а-дан кіші барлық мәндерінде , ал мәндерінде .

Д/уі: болса, онда мүмкін емес оқиға болады, олай болса, . Егер болса, онда ақиқат оқиға, демек, .

6. Егер кездейсоқ шама аралығындағы кез келген мәнді қабылдаса, онда болады.

7. Үздіксіз шаманың әрбір жеке мәніндегі ықтималдығы нөльге тең, яғни .

Мұны пайдаланып мынаны жазуға болады:

.

Ықтималдықтар үлестіруінің тығыздығы

Үздіксіз кездейсоқ шаманы ықтималдық тығыздығы (дифференциалдық функция) деп аталатын функциямен де беруге болады. интервалын алып, кездейсоқ шама Х-тің осы аралықта болу ықтималдығын анықтайық. Алдыңғы пункттегі 3-қасиет бойынша

бұл шама ықтималдықтың орташа тығыздығы делінеді. Егер

(2)

Бұл функция ықтималдық тығыздығы немесе ықтималдықтар үлестіруінің тығыздығы деп аталады.

Бұдан ықтималдық тығыздығы үлестіру функциясының туындысы екенін байқаймыз. Ал үлестіру функциясы болса, ықтималдық тығыздығы үшін бастапқы функция болып отыр. Сондықтан ықтималдық тығыздығы деу орнына ықтималдықтар үлестіруінің дифференциалдық заңы (функциясы деп те атайды). Үлестіру функциясын ықтималдық тығыздығы арқылы да анықтауға болады. Ньютон-Лейбниц формуласы бойынша

Үлестіру функциясының 3-қасиеті бойынша

десек, онда

(3)

Бұдан дифференциалдық функция пен интегралдық функция бірін-бірі анықтайтынын байқаймыз.

Үлестіру тығыздығы үлестіру функциясы сияқты үлестіру заңының бір түрі болып есептеледі. Бірақ үлестіру функциясы дискретті және үздіксіз кездейсоқ шамаларды сипаттайтын болғандықтан, олардың универсал заңы болады. Ал үлестіру тығыздығы болса, тек үздіксіз кездейсоқ шамаларды ғана сипаттайды.

Үлестіру тығыздығының қасиеттері:

1⁰. х-тің барлық мәнінде үлестіру тығыздығы теріс емес, яғни .

Бұл (2) теңдігінен тікелей шығады, өйткені кемімейтін функция, ал .

2⁰. Кездейсоқ шаманың мүмкін мәніндегі интервалдың барлық ұзындығы бойынша алынған үлестіру тығыздығының интегралы бірге тең, яғни

(4)

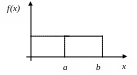
Мысалдар. 1. Бірқалыпты үлестіру

Егер ықтималдық тығыздығы

болса, онда Х кездейсоқ шамасының үлестіруін бірқалыпты делінеді.

Енді бойынша мәнін анықтайық. Егер болса, онда анықтамасы бойынша

болғанда

болғанда

Демек,

2. Үлестірудің нормаль (қалыпты) заңы.

Тығыздығы функциясы болған үздіксіз кездейсоқ шама ықтималдықтарының үлестіруін нормаль заң (үлестіру) делінеді. Мұндағы - математикалық күтім, - орташа квадраттық ауытқу деп аталатын параметрлер.

функциясы графигін нормаль қисық немесе Гаусс қисығы деп аталады. функциясының болғандағы дербес түрі функциясы толық зерттелген болатын.

Нормаль заңымен үлестірілген кездейсоқ шаманың интервалында болу ықтималдығы

формуласымен есептеледі.

Егер десек, онда .

Бұл тұжырымды үш алма ережесі деп атайды, оны нормаль заңға бағынатын кездейсоқ шаманың аралығынан шықпауын мейлінше бірге жуық ықтималдықпен айтамыз.