5 Дәріс. Толық ықтималдық формуласы. Байес формуласы

1. Сынауды қайталау

2. -нің жуық формуласы

3. Муавр-Лапластың интегралдық теоремасы

Сынауды қайталау

Ықтималдықтар теориясы мен оның қолданылуында осы уақытқа дейін қарастырылып келген жеке сынау нәтижесінің іс тұрғысынан қарағанда қажеттігі шамалы. Өйткені практика жүзінде жеке сынау нәтижесін алдын-ала болжау мақсат етілмейді. Мұның орнына сынаудың сан алуан қайталанып отыратын жағдайы мен осыған тиісті ықтималдықтарды есептеуді мақсат етеді. Осы айтылғандарды жай мысалдармен түсіндірейік.

Сынау жүргізгенде бірнеше нәтиженің пайда болуын күтуімізге болады. Бұлардың ішіндегі ең қарапайым сынау нәтижесі тек екі оқиға. А және оған қарама-қарсы болатын және әрбір тәуелсіз сынауда оқиғаның пайда болу ықтималдығы тұрақты (пайда болмауы ) тең болатын схемасы. Мұндай қарапайым схеманы тұңғыш қарастырған Швецаря ғалымы Я. Бернулли (1654-1705), сондықтан бұл схеманы Бернулли схемасы немесе тәуелсіз сынауларды қайталау схемасы деп атайды.

Мысал. Нысананы көздеп 3 рет оқ атылды. Әрқайсысының дәл тию ықтималдығы бірдей, яғни ол -ге тең. Нысанаға дәл екі оқтың тию ықтималдығы неге тең.

Шешуі: Оқтың нысанаға тиюуі А десек, тимеуі оқиғасы болады. Олардың ықтималдығы берілген шарт бойынша

Оқтың екі рет дәл тиюуі В оқиғасы болсын. Әрине, бұл күрделі оқиға.

Теорема. Егер әрбір сынауда оқиғаның пайда болу ықтималдығы тұрақты және ол р-ге тең болса, онда п рет тәуелсіз сынау жүргізгенде ол оқиғаның дәл т рет пайда болу ықтималдығы мынаған тең:

.

формуласын ықтималдықтардың биномдық үлестірімділігі не биномдық үлестірімділік заңы деп атайды.

-Нің жуық формуласы

Сынау саны п үлкен болған сайын ықтималдықта Бернулли формуласымен есептеу қиындай түседі. Сондықтан ғалымдар осы формула жарық көрісімен-ақ, оған жуық формулаларды іздестіре бастаған. п жеткілікті үлкен болғанда, ол р мәні 0 мен 1-ге мейілінше жуық болмаған жағдайда төмендегі формуланы пайдаланады:

(1)

мұнда

(2)

1. формуламен ықтималдықтың жуық мәнін табу өте оңай. Ол үшін

(3)

функциясының кестесін пайдаланамыз. (1-қосымша) функциясы симметриялы, яғни болғандықтан, кестеде х-тің оң мәндері ғана келтірілген. Сонымен, (1) формула

(4)

түрінде жазылады.

Муавр-Лапластың интегралдық теоремасы

Муавр-Лапластың теоремасы. Егер әрбір сынауда оқиғаның пайда болу ықтималдығы тұрақты және ол болса, онда сынау саны жағдайда оқиғаның орындалу санының және аралығында болу ықтималдығы

интегралына ұмытылады, яғни

(5)

болады, мұндағы

,

(5) теңдіктің оң жақ бөлігіндегі интеграл элементар функциялар арқылы есептелмейді. Сондықтан мына Лаплас функциясын енгіземіз:

(6)

Бұл функцияның таблицасы кітап соңында беріледі. (2-қосымша). Мұның қасиетін пайдалану арқылы (5) теңдікті ықшам түрде былай жазамыз:

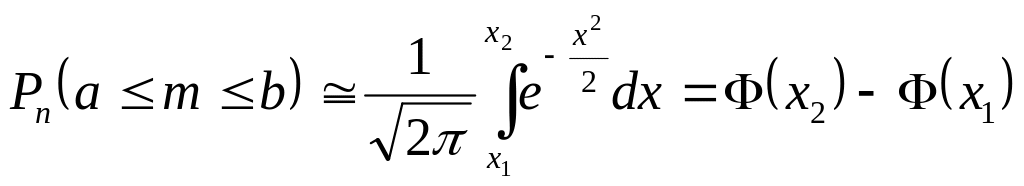(7)

немесе

(7^/)

Мұны Лапластың интегралдық формуласы дейміз.

Лаплас функциясының мынадай қасиеттері бар.

1. функциясы тақ функция, яғни .

2. функциясы монотонды өспелі, яғни болса, онда болады.

3. х шектеусіз өскенде функциясы 0,5-ке ұмтылады, яғни болады. Сондықтан .

4. қисығы координаталар бас нүктесіне қатысты симметриялы. Мұның екі горизонтал асимптотасы бар, өйткені ; . Ал болғанда .

5. функциясының мәні х-тің аз мәнінде де 0,5-ке жуық, сондықтан мәндерінде есептеудің қажеті жоқ. Таблицада х-тің 5-ке дейінгі мәні келтірілген.